VAE

VAE#

Introduction#

논문의 Introduction 에 다음과 같은 문구가 적혀있는데요.

“Variational Bayesian (VB) approach involves the optimization of an approximation to the intractable posterior”

이처럼 Variational Autoencoder 는 논문에서 제시하는 Auto-Encoding Variational Bayes(AEVB) 알고리즘 중 하나로, intractable 한 posterior 분포를 다루기 쉬운 뉴럴 네트워크로 근사함으로써 Variational Inference 를 하게 됩니다.

이가 의미하는 바가 무엇인지 한번 살펴보도록 하겠습니다.

Intractability#

Variational Autoencoder(VAE) 는 크게 Encoder 와 Decoder 부분으로 이루어져 있습니다. 더 자세하게는, Encoder는 입력 데이터 \(x\) 를 받아서 잠재변수(Latent Variable) \(z\) 를 만들어내고, Decoder 는 잠재변수 \(z\) 를 활용해서 다시 \(x\) 를 복원하게 됩니다.

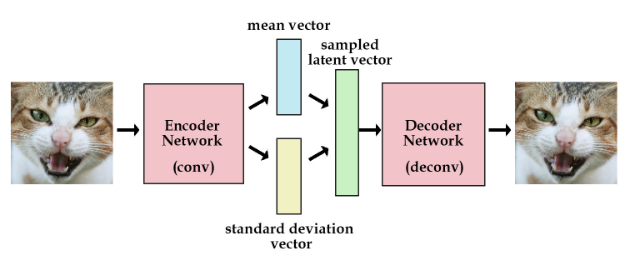
vae_01 — Fig. 1 Variational Autoencoder(VAE) Architecture#

Variational Autoencoder (VAE) 는 AutoEncoder 와 달리 확률 분포를 이용해 어떤 새로운 데이터를 생성하는 Decoder 부분에 초점을 둡니다. 이때 논문에서 다음과 같은 assumption 들을 내립니다. 첫번째로 \(p_{\theta}(z)\) 와 \(p_{\theta}(x|z)\) 는 parametric 한 distribution 을 가지고 있고, 이는 \(\theta\) 와 \(z\) 에 대해 differentiable 하다는 가정을 내립니다. 이 때, 대표적으로 \(p_{\theta}(z)\) 는 Gaussian distribution 을 따르고 \(p_{\theta}(x|z)\) 는 생성하고자 하는 데이터 성질에 따라 Bernoulli 혹은 Gaussian distribution 을 따르도록 정의합니다. 그리고 \(p_{\theta}(x|z)\) 의 파라미터 \(p\) 혹은 \((\mu, \sigma)\) 는 아래 그림과 같이 뉴럴 네트워크로 구성된 Decoder 로부터 계산이 됩니다.

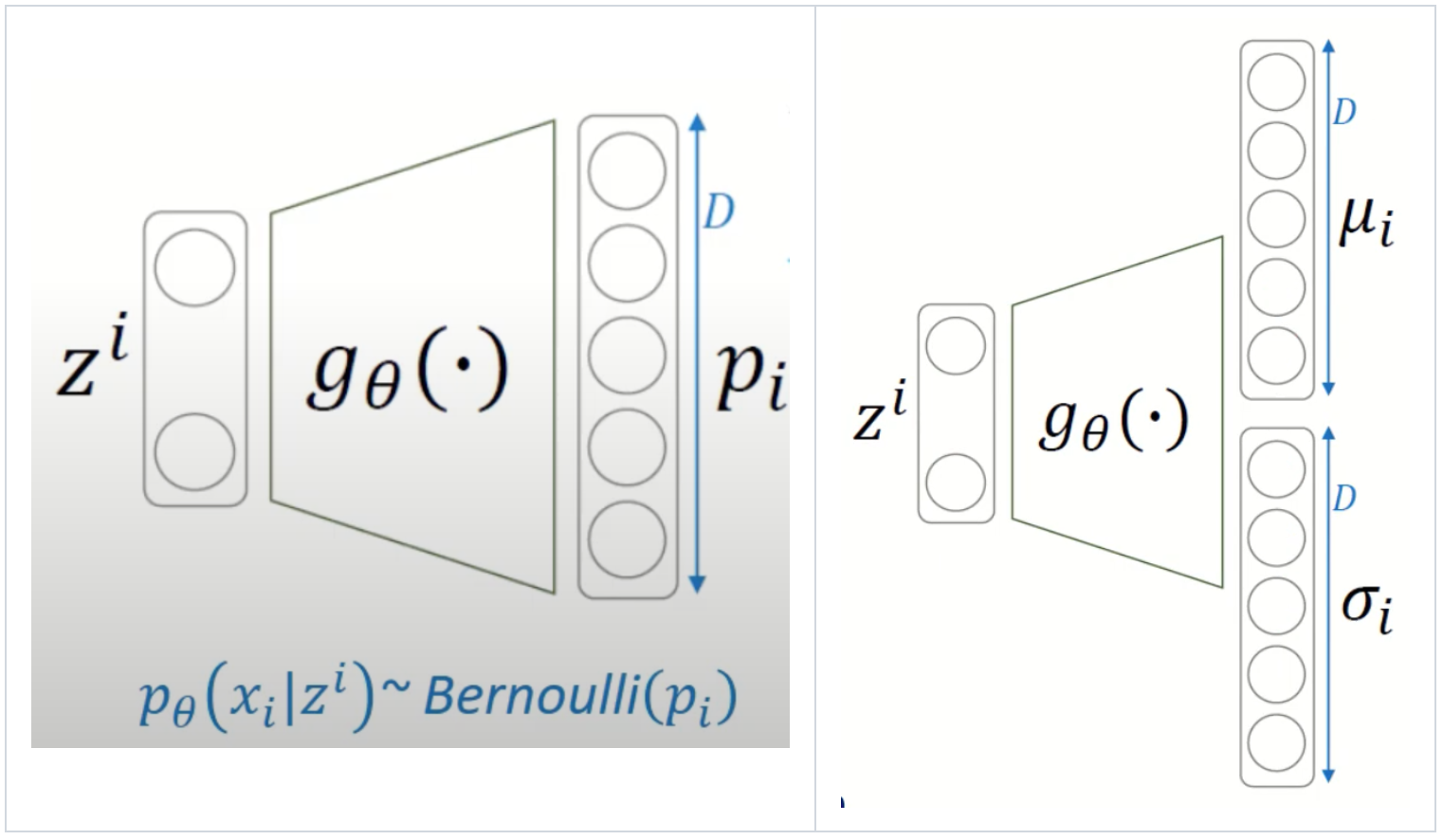
vae_07 — Fig. 2 Overview of Bernoulli(left) and Gaussian(right) Decoder#

이를 기반으로 우리는 ML/MAP estimation 을 통해 marginal likelihood \(p_{\theta}(x)\) 를 최대화시키는 파라미터 \(\theta\) 를 구하는 것이 목적입니다. 하지만, \(p_{\theta}(x) = \int p_{\theta}(z)p_{\theta}(x|z) \ dz\) 는 intractable 하기 때문에 \(p_{\theta}(z|x)\) 를 계산하기 위한 Encoder 가 등장하게 됩니다.

\[ p_{\theta}(x) = p_{\theta}(x|z)p_{\theta}(z)/p_{\theta}(z|x) \]

여기서 \(p_{\theta}(z|x)\) 역시 intractable 하기 때문에 이를 잘 근사화하는 뉴럴 네트워크 \(q_{\phi}(z|x)\) 를 정의하게 되고, 이러한 과정을 변분추론(Variational Inference) 라고 합니다. 아래는 Encoder 와 Decoder 를 함께 도식화한 그림입니다. 정리하자면, MLP Encoder 를 통해 계산된 \(\mu\) 와 \(\sigma\) 로 잠재변수 \(z\) 를 생성하게 되고, 이를 기반으로 Decoder 는 원본 이미지와 유사한 데이터를 생성하게 됩니다.

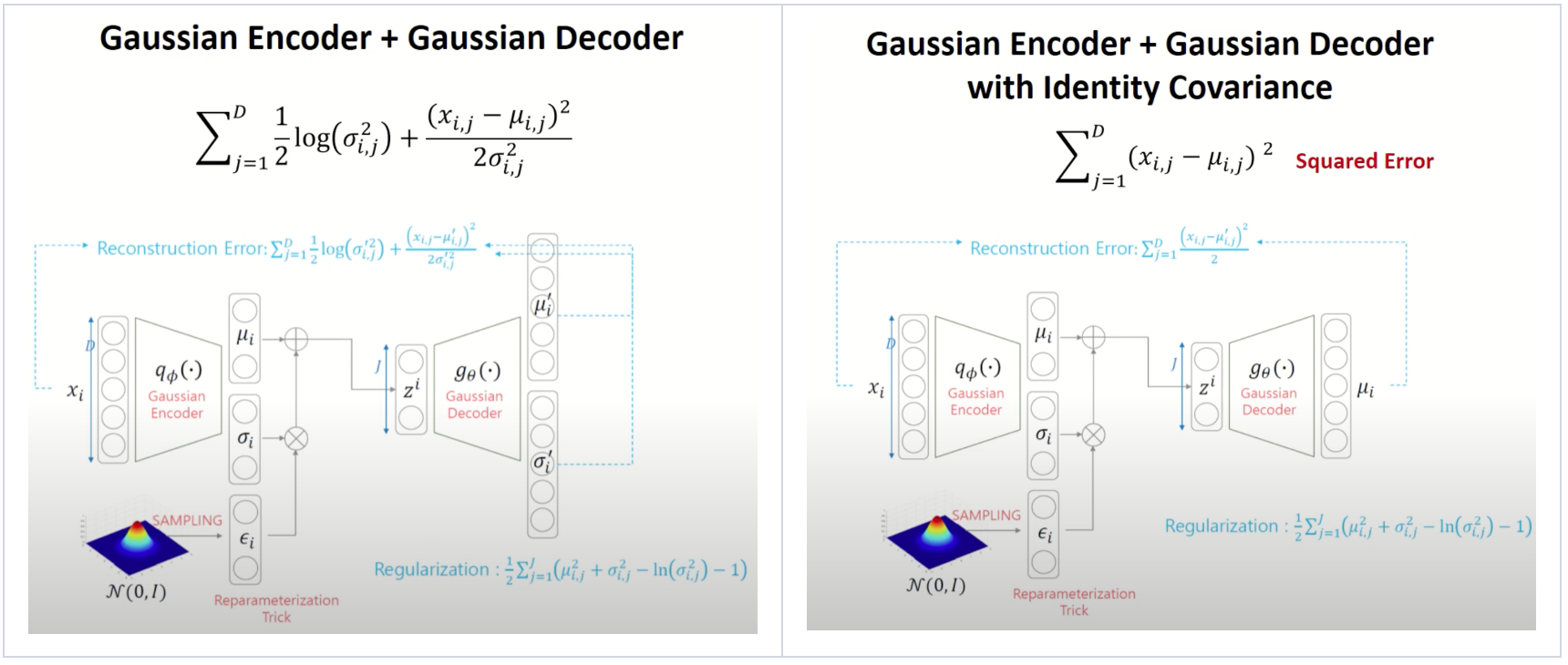
vae_08 — Fig. 3 Overview of Gaussian Encoder and Decoder#

해당 implementation code 도 확인해보겠습니다.

Encoder 구현 code

class Encoder(nn.Module):
    def __init__(self):
        super(Encoder,self).__init__()
        self.fc1_1 = nn.Linear(784, hidden_size)
        self.fc1_2 = nn.Linear(784, hidden_size)
        self.relu = nn.ReLU()
                        
    def encode(self,x):
        x = x.view(batch_size,-1)
        mu = self.relu(self.fc1_1(x))
        log_var = self.relu(self.fc1_2(x))
                
        return mu,log_var
    
    def reparametrize(self, mu, logvar):
        std = logvar.mul(0.5).exp_()
        
        eps = torch.FloatTensor(std.size()).normal_()
        eps = Variable(eps).cuda()
        
        return eps.mul(std).add_(mu)
    
    def forward(self,x):
        mu, logvar = self.encode(x)
        reparam = self.reparametrize(mu,logvar)
        
        return mu,logvar,reparam

Decoder 구현 code

class Decoder(nn.Module):
    def __init__(self):
        super(Decoder,self).__init__()
        self.fc1 = nn.Linear(hidden_size, 784)
        self.sigmoid = nn.Sigmoid()
    
    def forward(self,x):
        out = self.fc1(x)
        out = self.sigmoid(out)
        out = out.view(batch_size,28,28,1)
        
        return out

SGVB(Stochastic Gradient Variational Bayes)#

이로써 우리는 marginal likelihood \(p_{\theta}(x)\) 를 최대화시키는 파라미터 \((\theta, \phi)\) 를 찾으면 되고, 이에 대한 lower bound 를 수식적으로 표현하면 손실함수(loss function) 를 다음과 같이 Reconstruction Error 와 Regularization term 로 분할할 수 있습니다.

\[ L(\theta, \phi;x_i) = \arg \min_{\theta, \phi} \sum_{i} -\mathbb{E}\_{q_{\phi}(z|x_i)}[\log(p(x_i|g_{\theta}(z))] + KL(q_{\phi}(z|x_i)||p(z)) \]

Reconstruction Error 는 Decoder 에서 생성하는 데이터가 최대한 원본 데이터와 유사하도록 하는 term 이고, Regularization 은 Encoder 에서 만드는 잠재변수의 분포가 저희가 부여한 prior distribution 이랑 가깝도록 설정하는 term 입니다. 이때, Reconstruction Error 는 다음과 같은 Monte Carlo Estimator \(\tilde{\mathcal{L}}^{B}\) 로 근사값을 구할 수 있고, 하나의 sample 을 계산하는 것도 연산량이 많으므로 논문에서는 sample size \(L\) 을 1 로 설정합니다.

\[ \tilde{\mathcal{L}}^{B}(\theta, \phi; x^{(i)})=-D_{KL}(q_{\phi}(z|x^{(i)})||p_{\theta}(z))+\frac{1}{L}\sum^{L}_{l=1} \log p\_\theta (x^{(i)}|z^{(i,l)})) \]

Lower bound 에 대한 수식을 변환하여 수식 전체에 대한 Monte Carlo Estimator \(\tilde{\mathcal{L}}^{A}\) 로도 근사값을 구할 수 있는데 이는 평균적으로 \(\tilde{\mathcal{L}}^{B}\) 에 비해 variance 가 높다고 합니다.

\[ \tilde{\mathcal{L}}^{A}(\theta,\phi;x^{(i)})=\frac{1}{L}\sum^{L}_{l=1}\log p_{\theta}(x^{(i)},z^{(i,l)})-\log q_{\phi}(z^{(i,l)}|x^{(i)}) \]

Reparameterization Trick#

논문에서는 모델 학습 시 backpropagation 을 원활히 사용할 수 있도록 reparameterization trick 을 소개합니다. 잠재변수 \(z\) 를 Encoder 에서 나온 \(\mu\) 와 \(\sigma\) 로 직접 샘플링하지 않고, backpropagation 이 가능하도록 Gaussian noise 를 우선적으로 샘플링하고 해당 \(\mu\) 와 \(\sigma\) 를 각각 더하고 곱하게 됩니다. 이는 \(q_{\phi}(z|x)\) 이 Gaussian distribution 을 따른다고 설정했을 때이고, \(q_{\phi}(z|x)\) 에 대해 다른 분포를 가정하여 그에 따른 다른 reparameterization trick 을 시도할 수 있다고 논문에 명시되어 있습니다.

하단에는 Gaussian 분포에 대한 reparameterization trick 를 도식화한 그림입니다. 왼쪽에는 reparameterization trick이 적용되지 않은 경우로 \(\mu\) 나 \(\sigma\) 값이 고정되어 있어도 \(\mathcal{N}(\mu,\sigma^2)\) 에서 샘플링하므로 \(z\) 는 랜덤한 값이 되고 loss function 을 \(\mu\) 나 \(\sigma\) 에 대해 미분할 수 없어 backpropagation 을 적용하기가 어렵습니다. 반면에, 오른쪽처럼 reparameterization trick 을 적용하면, \(z\) 가 deterministic 한 형태로 정의되고 \(\mu\) 나 \(\sigma\) 에 대한 변수로도 미분이 가능해지기 때문에 backpropagation 을 활용하여 모델을 학습시킬 수 있습니다.

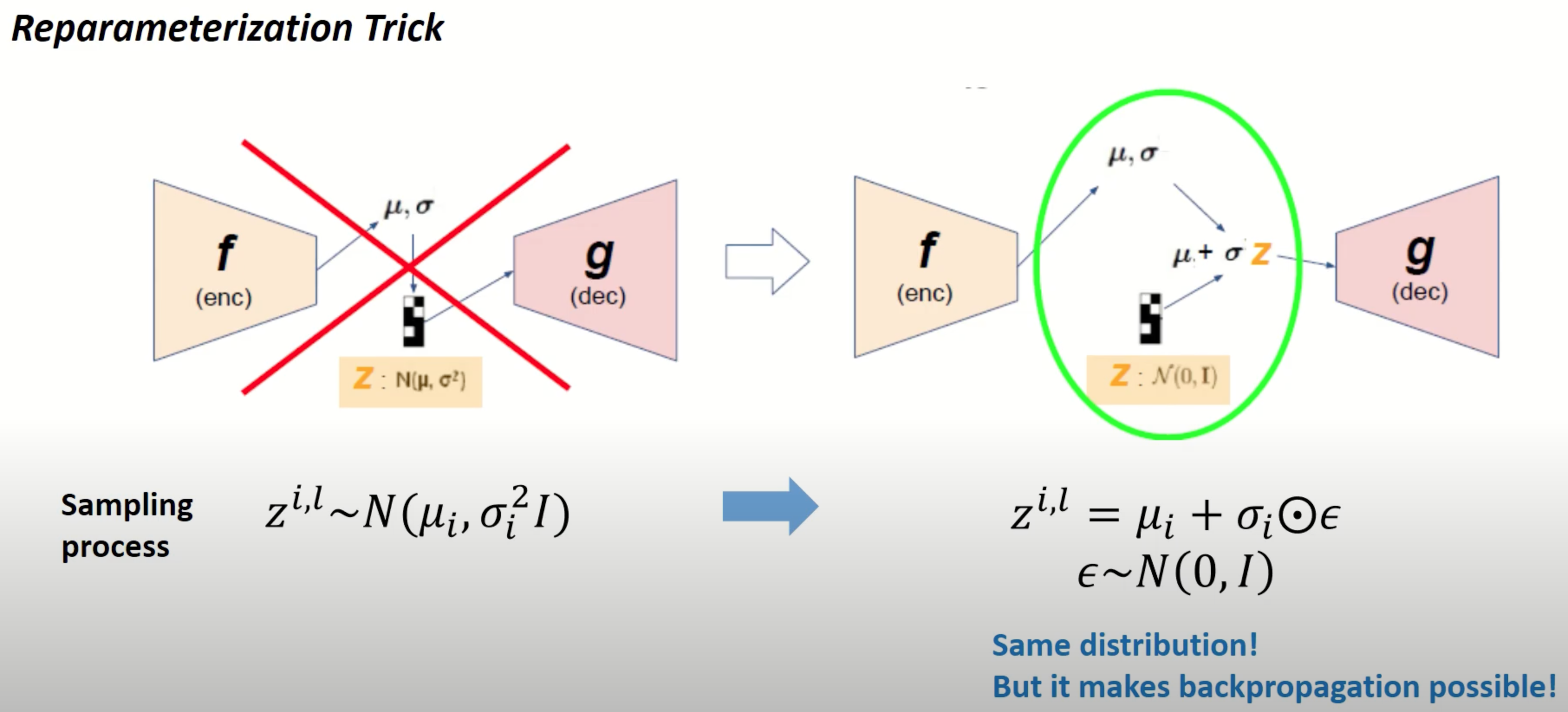
vae_05 — Fig. 4 Overview of Reparameterization Trick#

Training Algorithm#

모델을 학습하는 전체적인 과정은 아래와 같습니다.

vae_09 — Fig. 5 Overview of Training Algorithm#

Experiments#

논문에서는 MNIST 와 Frey Face 데이터셋에 대해 AEVB(Auto-Encoder variational Bayesian)와 wake-sleep 알고리즘를 적용해서 비교합니다. 여기서 Frey Face 데이터셋은 continuous 하므로 Gaussian Decoder 를 사용합니다. 실험결과는 아래 그림과 같습니다.

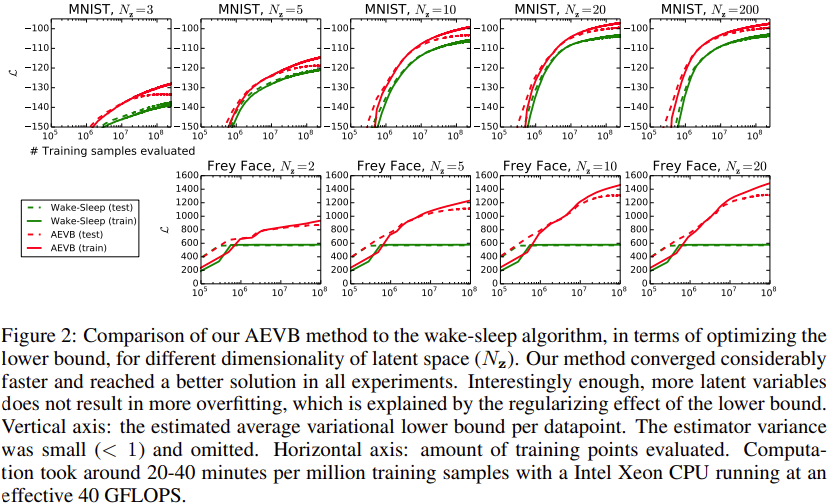
vae_10 — Fig. 6 Experimental Results - Likelihood lower bound#

해당 그림처럼 lower bound 를 최적화하는데 AEVB 알고리즘이 더 빠르게 수렴하며 모든 실험에서 성능적으로도 더 나은 부분을 확인할 수 있습니다.

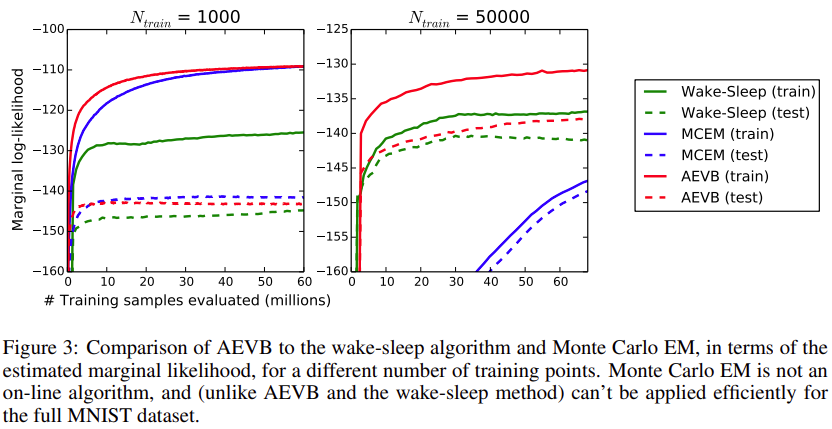
vae_11 — Fig. 7 Experimental Results - Marginal likelihood#

또한, latent variable \(z\) 의 차원이 작으면 marginal likelihood 를 직접 Monte Carlo EM 을 할용하여 구할 수 있는데, 이에 대한 결과도 논문에서 보여줍니다. Monte Carlo EM 의 경우 학습 데이터가 많으면 수렴이 되지 않는 부분을 확인할 수 있습니다.

Summary#

AutoEncoder 는 latent space 에 하나의 값으로 지정해줬다면, VAE 는 평균 그리고 분산 파라미터들과 Gaussian 분포를 가진 샘플을 통해 잠재변수를 생성합니다. 그리고 VAE 를 실제로 사용해보면 생성된 데이터 image quality 가 낮다는 단점을 가지고 있다고 합니다.

VAE

Contents