Information

• Title: Shap-E: Generating Conditional 3D Implicit Function

• Reference

  • Paper: https:arxiv.org/abs/2305.02463

  • Code: https:github.com/openai/shap-e

• Author: Kyeongmin Yu

• Last updated on July. 18. 2024

Shap-E

Fig. 676 Shap-E를 통해 생성한 3D assets

0. Abstract

📌 논문요약
2023년 openai의 Heewoo Jun, Alex Nichol 가 발표한 논문입니다. official code는 github에서, diffusers를 활용한 코드는 huggingface에서 확인할 수 있습니다.
목적 - 조건부 3D assets 생성
생성방식 - encoder를 통해 implicit function의 parameter 형태로 표현한 후, 이를 diffusion model의 조건으로 사용함으로써 conditional 3D assets을 생성할 수 있도록 했다.
차별점 - texture mesh 나 NeRF 모두 생성 가능한 implicit function의 parameters를 직접적으로 생성할 수 있다. (다른 3D 생성 모델의 경우 단일 표현만 가능한 경우가 많다고 합니다.)

1. Introduction

implicit neural representations (INRs)는 3D assets을 인코딩하는 방식으로 많이 사용된다. 3D asset을 표현하기 위해 INRs는 주로 3D coordinate를 location specific info(density, color)로 맵핑한다. 일반적으로 INRs는 화질에 영향을 받지 않는데 이는 고정된 grid나 sequence가 아닌 arbitrary input points를 처리할 수 있기 때문이다. 덕분에 end-to-end 미분이 가능하다. INRs은 이후 다양한 downstream applications도 가능하게 한다. 본 논문에서는 2가지 타입의 INRs을 다룬다.

• Neural Radiamce Field (NeRF) - 3D scene을 function mapping으로 표현.

  • coordinate, viewing direction \(\rightarrow\) density, colors along camera rays

• textured 3D mesh (DMTet, GET3D)

  • coordinate \(\rightarrow\) colors, signed distances, vertex offsets

  • INRs는 삼각메쉬를 생성할 때 사용될 수 있다.

이미지, 비디오, 오디오, 3D assets 생성에 관한 다양한 연구가 있지만 downstream application에서 사용하기 편한 형태로 3D assets을 표현하는 방법에 대한 연구는 부족하다. 본 논문은 단일 representation으로 부터 두가지 형태로 rendering 가능하게 했다는 특징이 있다.

2. Background

2.1 Neural Radiance Fields (NeRF)

Mildenhall et al. 는 아래와 같이 NeRF(3D scene을 implicit function으로 표현하는 방법)를 제안했다.

\[ F_{\Theta} : (\mathbf{x},\mathbf d)↦(\mathbf c,\sigma) \tag{1} \]

\(x\) 는 3D 공간 좌표, \(d\) 는 3D 시야 각도, \(c\) 는 RGB, \(\sigma\) 는 density(\(\ge 0\)) 이다. \(F_\Theta\) 는 편의를 위해 \(\sigma(x)\) 와 \(c(x,d)\) 두개의 식으로 나누어 표현했다.

새로운 시야에서 바라본 scene 을 렌더링하기 위해서, 아래와 같이 각 ray에 맞는 color값을 계산한다.

\[ \hat C(\mathbf r)=\int^\infty_0 T(t)\sigma(\mathbf R(t))\mathbf c(\mathbf r(t),\mathbf d)dt, \space \text{where} \space T(t)=\text{exp}\Big(-\int^\infty_0 \sigma(\mathbf r(s))ds\Big) \tag{2} \]

• 수식(2) 설명

  

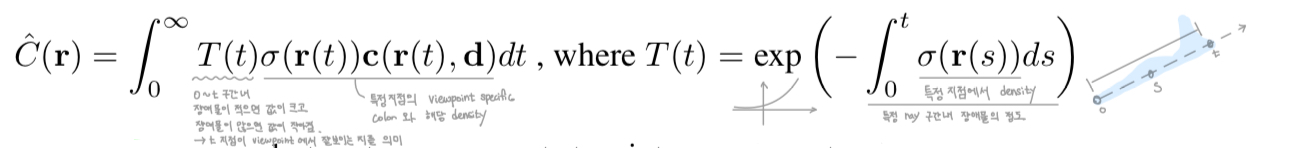
  Fig. 677 수식 (2) 보충설명

위의 적분식을 아래와 같이 discrete sum으로 간략화 할 수 있다.

\[ \hat C(\mathbf r)=\sum^N_{i=1} T_i(1-\text{exp}(-\sigma(\mathbf r(t_i))\delta_t))\mathbf c (\mathbf r(t_i),\mathbf d), \space \text{where} \space T_i=\text{exp}\Big(-\sum^{i-1}_{j=1} \sigma(\mathbf r(t_j))\delta_j\Big) \tag{3} \]

구간을 나누는 방식은 중요한 부분으로 coarse와 fine 두단계로 나누어 더 세부적으로 sequence를 나눈다. 2개의 NeRF 모델을 이용하여 2번의 sampling을 한다.

\[ w_i \sim T_i(1-\text{exp}(-\sigma(\mathbf r(t_i))\delta_i))\tag{4} \]

본 논문에서는 ray의 transmittance를 아래와 같이 추가적으로 정의하였다. 이는 직관적으로 ray의 alpha값이나 opacity의 총합에 해당한다.

\[ \hat T(\mathbf r)=1-\text{exp}\Big(-\sum^N_{i=1}\sigma(\mathbf r(t_i))\delta_i\Big)\tag{5} \]

• 수식(5) 설명

  

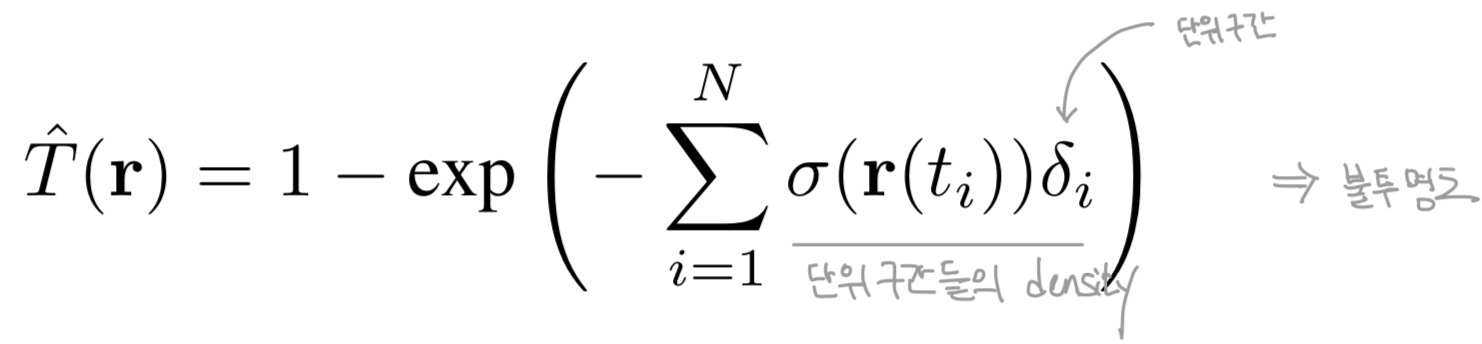
  Fig. 678 수식 (5) 보충 설명

2.2 Signed Distance Functions and Texture Field (STF)

본 논문에서 STF는 signed distances와 texture colors 두가지 모두를 생성하는 implicit function을 의미한다. 이번 섹션에서는 이러한 implicit function이 meshes를 구성하고 rendering을 만드는 방식을 설명한다.

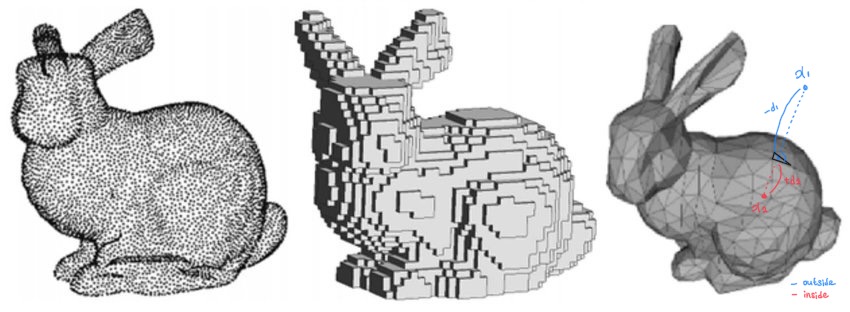
Fig. 679 point cloud, voxel, polygon mesh의 비교
source - 3D Vision with Transformers: A Survey

**Signed Distance Functions (SDFs)**는 3D shape을 scaler field에서 표현하는 전통적인 방법중 하나다. 특히 SDF \(f\)는 coordinate \(x\)를 scaler 로 mapping한다. (\(f(\mathbf x)=d\)) 여기서 \(d\)는 특정 위치 \(x\)에서 가장 가까운 물체의 표면까지의 거리를 말한다. \(d\)가 0보다 작으면 해당 물체 외부임을 의미한다. 이러한 정의에 따라 \(f(\mathbf x)=0\) 일때는 물체의 표면을 의미한다. \(\text{sign}(d)\)는 표면에 따른 normal orientation을 의미한다.

• DMTet : SDFs를 활용하여 3D shape을 생성하는 모델. coarse voxel을 입력으로 받아 synthesized shape(SDF, tetrahedral)을 만들어 낸다. DMTet의 출력은 dense spatial grid에서의 각 vertex \(v_i\)별 SDF 값 \(s_i\)와 displacement \(\vartriangle v_i\) 이다. 이후 설명 생략

• GET3D : DMTet에 추가적인 texture 정보까지도 생성하는 모델이다. 물체의 표면의 지점 \(p\) 마다 RGB color를 예측하는 모델을 따로 학습시켜 texture를 만들었다. 이후 설명 생략

Fig. 680 texture, bump, displacement의 비교
source - tutorials in grabcad

bump는 lighting 을 고려하여 texture가 더 자연스러워 졌지만 구의 표면을 보면 물체의 형태가 실제로 바뀐것은 아님을 알수 있다.displacement를 보면 texture를 따라 물체의 표면이 변화된것을 볼 수 있다.

2.3 Diffusion Models

본 논문에서 활용한 diffusion model은 DDPM으로 diffusion process(noising process)를 data sample \(x_0\) 에 gaussian noise를 서서히 추가하여 완전한 노이즈가 되어가는 과정 \((x_1,x_2,…x_T)\) 으로 표현했다. 일반적으로 \(x_T\)는 gaussian noise와 구분불가능한 상태로 상정한다. 해당 과정은 sequential하게 진행되지만 활용시에는 아래의 식과 같이 특정 단계로 바로 “jump”하는 방식을 이용한다.

\[ x_t=\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon\tag{6} \]

\(\epsilon\) 은 랜덤한 노이즈를 의미하고, \(\bar\alpha_t\)는 단조감소하는 노이즈 스케줄을 의미한다. (\(t=0\) 일때는 sample data가 되어야 하므로 \(\bar\alpha_0=1\))

모델 \(\epsilon_\theta\)를 학습할때는 아래의 손실함수를 사용한다.

\[ L_{\text{simple}}=E_{x_0\sim q(x_0),\epsilon\sim\mathcal N(0,\mathbf I),t\sim U[1,T]}\|\epsilon -\epsilon_\theta (x_t,t)\|^2_2\tag{7} \]

아래와 같이 표현할 수도 있는데 Shap-E 논문에서는 아래의 식을 활용하였다. 위는 (모델이 예측하는 노이즈, diffusion process에서 더해진 노이즈)의 차이를 줄이는 방향으로 학습한다는 의미이고, 아래는 (data sample \(x_0\), 모델이 예측한 노이즈를 제거하여 만든 이미지)의 차이를 줄이는 방향으로 학습한다는 의미이다.

\[ L_{x_0}=E_{x_0\sim q(x_0),\epsilon\sim\mathcal N(0,\mathbf I),t\sim U[1,T]}\|x_\theta (x_t,t)-x_0\|^2_2\tag{8} \]

denosing시에는 높은 퀄리티와 적당한 latency를 위해 Heun sampler와 classifier-free guidance를 사용했다.

\[ \hat x_\theta(x_t,t|y)=x_\theta(x_T,t)+s\space\cdot\space (x_\theta(x_t,t|y)-x_\theta(x_t,t)) \tag{9} \]

\(s\) 는 guidance scale이고 \(s=0, s=1\) 일때는 regular unconditional, conditional sampling을 뜻한다. \(s\) 를 더 키우면 일관성(coherence)은 커지지만 다양성(diversity)이 떨어질 수 있다. 실험적으로 나은 결과물을 얻기 위해서는 guidance가 필요하다는 것을 알아냈다. (section 5의 figure 4 참고)

2.4 Latent Diffusion

continuous latent space에서도 diffusion을 활용하여 샘플들을 생성할 수 있다. 이는 Stable Diffusion(LDM)에서 제안된 것으로, pixel space와 latent space간의 변환을 담당하는 encoder와 decoder를 추가하여 two-stage방식으로 모델을 학습시키면 된다. 앞서 봤던 노이즈를 예측을 담당하는 모델 \(\epsilon_\theta\)는 latent space에서 추가된 노이즈(latent noise)를 예측하게 되는 것이다. original LDM에서는 latent noise를 원본 이미지 보다 낮은 복잡도(lower-dimensional distribution)를 가지도록 KL penalty나 vector quantization layer를 사용했다.

본 논문에서도 위와 유사한 방식을 사용했으나 GAN-based objective와 perceptual loss를 사용하지 않고 단순히 \(L_1\), \(L_2\) reconstruction loss를 사용했다. 또한 KL regularization과 vector quantization은 bottleneck이 되므로 고정된 numerical range를 가지도록 하고 diffusion style의 noise를 추가 했다.

3. Related Work

• Point-E

• 3D auto-encoder + implicit decoder

  • Fu et al. [16] - SDF sample grid를 encode, implicit decoder의 condition으로 사용.

  • Sanghi et al. [54] - voxel grid를 encode, implicit occupancy network의 condition으로 사용.

  • Liu et al. [34] - voxel-based encoder와 implicit occupancy, color decoder를 학습.

  • Kosiorek et al. [30] - rendered view을 encode, encoding된 latent vector를 NeRF의 condition으로 사용.

  • Chen and Wang [6] - transformer기반 모델을 사용하여 rendered view에서 MLP parameter를 곧바로 생성.

• 학습된 encoder 없이 implicit 3D representation을 생성하는것을 목표로 하는 모델들

  • Park et al. [43] - auto decoder를 학습. 데이터셋 내의 각 샘플의 embedding vector table을 학습.

  • Bautista et al. [4] - NeRF decoder를 조건으로 scene 별 latent code를 학습.

  • Dupont et al. [12] - implicit function을 학습하기 위해 meta learning 활용.

  • Erkoç et al. [14] - implicit MLP weight를 곧바로 생성하기 위해 diffusion을 활용.

  • akin to [12] - NeRF parameter fitting을 필요로 함.

  • Wang et al. [66] - 데이터셋 내의 각 샘플의 개별 NeRF를 joint 학습.

4. Method

📌 훈련 방법
two stage 방식으로 Shap-E를 학습시킨다.
Stage 1. train an encoder
Stage 2. train a conditional diffusion model on outputs of the encoder

4.1 3D Encoder

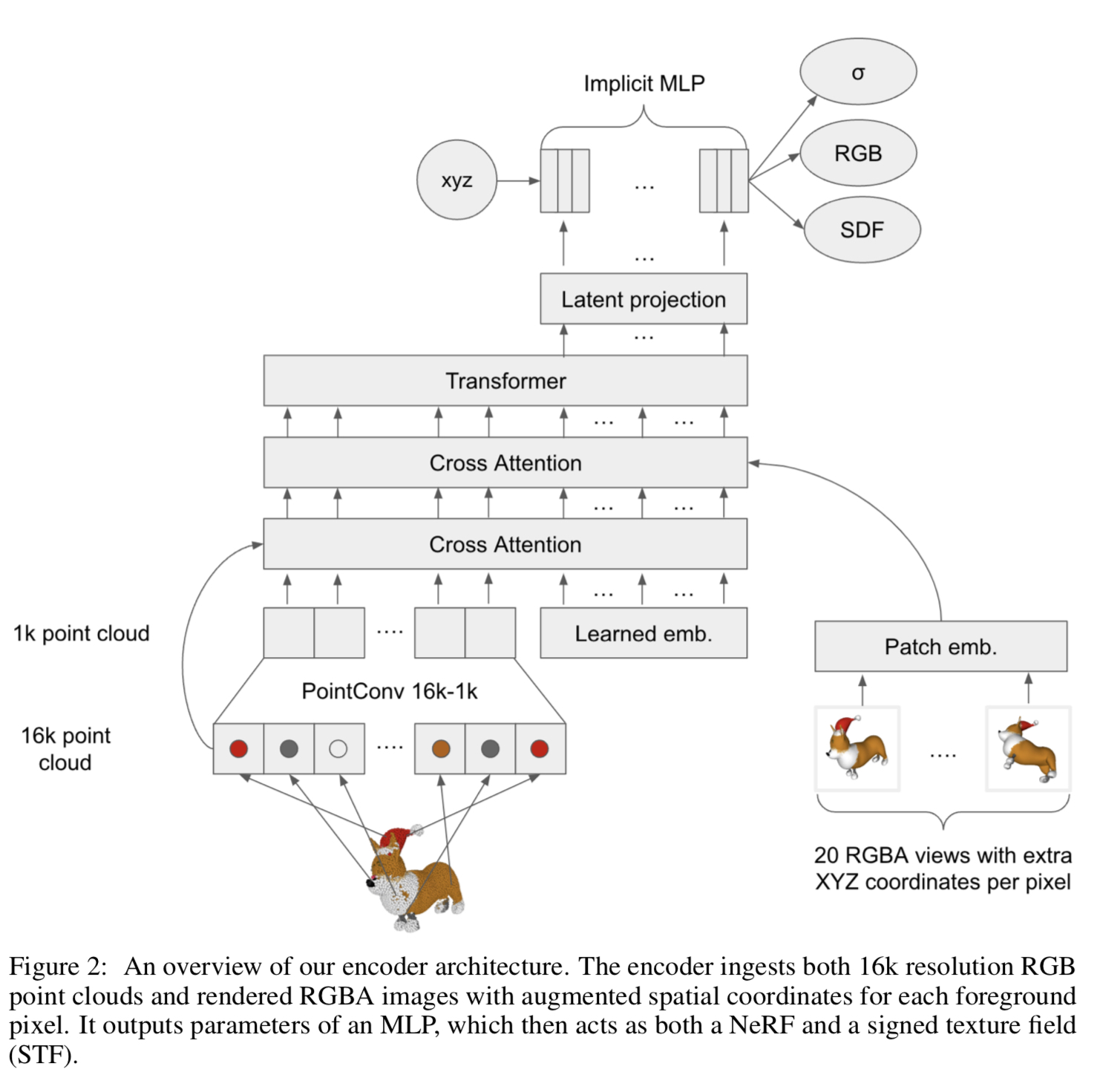
Fig. 681 3D Encoder의 구조

encoder의 input : (point clouds, rendered views)
encoder의 output : MLP의 parameter

입력 representation의 세부 특성
Point-E와 비교하였을때, post-processing 방식을 변경하여 3D Asset별 사용하는 RGB point cloud의 point 개수를 늘이고, 더 많은 view를 256x256 크기로 렌더링 하여 사용했다. 구체적으로는 다음과 같다.

• Point Clouds: 기존 4K -> 16K

• Multiview point clouds: 기존 20 views -> 60 views (20개의 view를 사용한 경우 생성된 pointcloud에 crack이 발생했다고 함)\ view 렌더링시 조명과 물체표면의 특성을 간략화했다.

encoder에서 얻은 parameter는 implicit function에서 asset의 representation을 의미한다. (+의미상 다양한 형태로 입력받은 3D asset의 특성을 융합하여 하나로 표현한 것, 논문의 장점으로 NeRF와 point cloud 모두를 얻을수 있다고 했으므로 상당히 의도가 느껴지는 입력으로 보인다. )

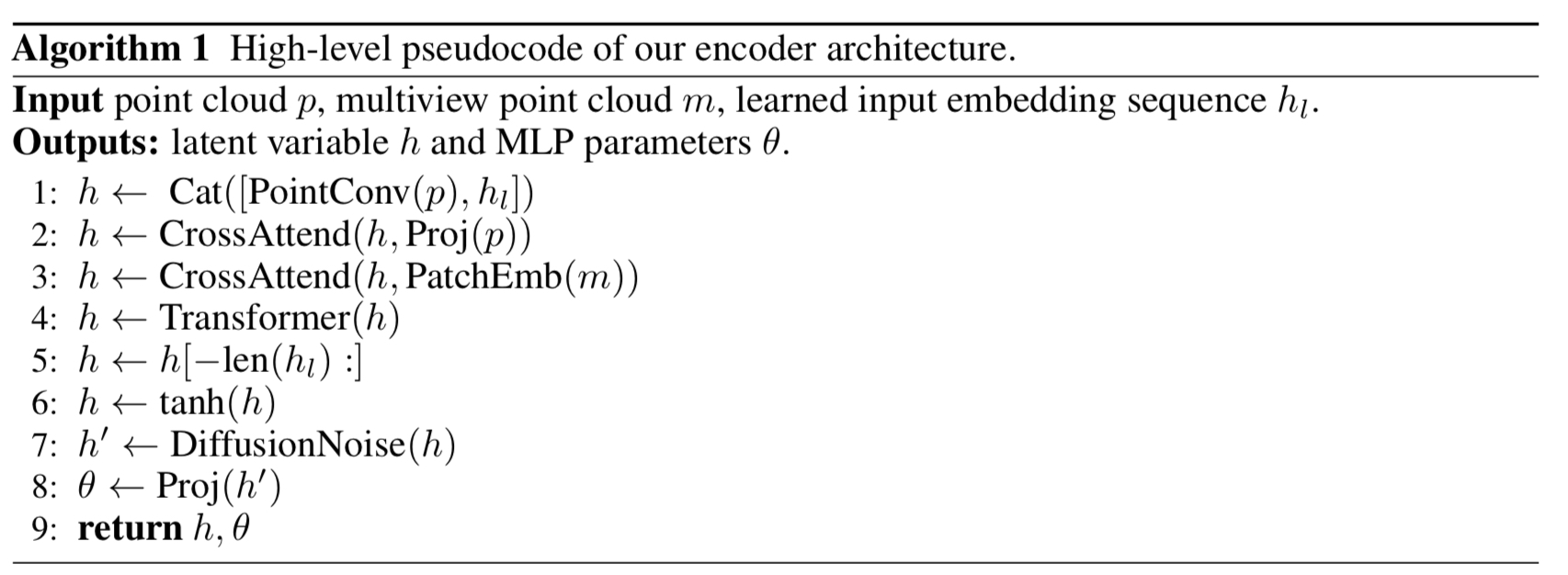
Fig. 682 pseudocode

encoder에 입력된 point clouds와 views는 cross-attention과 transformer backbone에 의해 처리되어 sequence of vectors가 된다. 이후 latent bottleneck과 projection layer를 통과하여 MLP weight matrices를 만든다.

encoder는 NeRF rendering objective를 사용(Section 4.1.1 참고)하여 사전 학습한다. mesh-based objective를 이용한 사전학습시 보다 더 안정적인 결과물을 얻을 수 있었다고 한다. 이후에는 SDF와 texture color prediction을 위해 추가적인 output head를 넣어 Section 4.1.2와 같이 two-stage 방식으로 head들을 학습시킨다.

4.1.1 Decoding with NeRF Rendering

original NeRF의 식과 유사하지만 coarse net과 fine net이 parameter들을 공유할 수 있도록 하지는 않았다. 랜덤한 4096개의 ray를 각 학습 데이터에서 샘플링하였으며, \(L_1\) loss가 최소가 되도록 했다. (original NeRF에서는 \(L_2\) loss를 사용)

\[ L_{\mathbf{RGB}}=E_{\mathbf r\in R}[\|\hat C_c(\mathbf r)-C(\mathbf r)\|_1+\|\hat C_f(\mathbf r)-C(\mathbf r)\|_1] \tag{10} \]

여기에 추가적으로 각 ray의 transmittance에 대한 손실함수를 추가했다. 특히, 한 ray의 density 적분값(integrated density)을 통해 얻은transmittance로 coarse rendering과 fine rendering시 \(\hat T_c(r)\) 와 \(\hat T_f(r)\)를 예측하였다. ground truth로는 gt rendering결과의 alpha channel을 사용하였다. 이 손실함수는 아래와 같이 표현할 수 있다. (+NeRF의 경우 novel view를 만드는 것이 목적이었으나 본 논문은 mesh도 생성해야 하므로 노이즈 제거가 더욱 중요하였을 것으로 생각된다.)

\[ L_T=E_{\mathbf r\in R}[\|\hat T_c(\mathbf r)-T(\mathbf r)\|_1 +\|\hat T_f(\mathbf r)-T(\mathbf r)\|_1]\tag{11} \]

최종적으로는 두 손실함수를 합하여 최적화를 진행하였다.

\[ L_\text{NeRF}=L_\text{RGB}+L_T \tag{12} \]

4.1.2 Decoding with STF Rendering

Fig. 683 texture, bump, displacement의 비교
source - https:grabcad.com/tutorials/adding-textures-to-3d-models-texture-bump-and-displacement-mapping-how-to-make-photo-realistic-models

NeRF 방식을 통해 사전학습한 후, MLPs에 STF output heads를 추가한다. 이러한 MLPs는 SDF와 texture color를 예측한다. triangle mesh를 생성하기 위해서는 각 vertex의 SDF를 regular \(128^3\) grid로 옮겨 미분가능한 형태의 Marching Cube를 진행해야 한다. 이후 texture color는 최종 mesh의 각 vertex texture color head를 통해 얻는다. Pytorch 3D를 활용하면 미분가능한 rendering을 통해 textured mesh를 얻을 수 있다고 한다. 렌더링 시에는 데이터셋 구축시 preprocessing에 사용한 것과 동일한 lighting 조건을 사용했다.

사전 실험시 랜덤 초기화된 STF output heads를 사용했을 때는 결과가 불안정 했으며, rendering based objective를 사용하여 학습하는 것이 어려웠다. 해당 문제를 완화하기 위해 SDF와 texture color를 해당 output heads를 직접 학습시키기 전에 distill 접근법을 사용했다. Point-E의 regression model을 활용하여 입력 좌표를 랜덤하게 샘플링하고, SDF distillation target을 구했다. 그리고 RGB target로는 asset RGB point cloud에서 특정위치 \(x\)와 가장 가까운(nearest neighbor) point의 색을 사용했다. distillation training 시 distillation loss와 NeRF loss를 더하여 사용했다.

\[ L_\text{distill}=L_\text{NeRF}+E_{\mathbf x\sim U[-1,1]^3}[\|\text{SDF}_\theta(\mathbf x)-\text{SDF}_\text{regression}(\mathbf x)\|_1+\|\text{RGB}_\theta(\mathbf x)-\text{RGB}_\text{NN}(\mathbf x)\|_1] \tag{13} \]

STF output heads가 distillation을 통해 적절한 초기값을 갖게된 후, NeRF encoder와 STF rendering 전체를 end-to-end로 fine-tune한다. 실험적으로 STF rendering에는 \(L_1\)을 사용하는 것은 불안정했으므로 \(L_2\) 손실함수만 사용하는 것이 이러한 rendering 방식에 적절함을 알 수 있었다. STF rendering에 사용한 loss는 아래와 같다.

\[ L_\text{STF}=\frac{1}{N\space \cdot\space s^2}\sum^N_{i=1}\|\text{Render}(\text{Mesh}_i)-\text{Image}_i\|^2_2\tag{14} \]

• mesh를 렌더링한 이미지와 target 이미지의 L2 reconstruction loss의 평균

N은 이미지 개수, s는 이미지의 화질, \(\text{Mesh}_i\)는 \(\text{sample}_i\)의 constructed mesh를 말한다. \(\text{Image}_i\)는 RGBA rendering된 결과물로 alpha채널을 포함하고 있기 때문에 transmittance에 대한 loss를 따로 추가하지 않았다.

최종 fine-tuning 단계에서는 아래와 같이 더한 objective function을 사용한다.

\[ L_\text{FT}=L_\text{NeRF}+L_\text{STF}\tag{15} \]

4.2 Latent Diffusion

Point-E의 transformer 기반 diffusion 구조를 채택했다. 하지만 point cloud를 latent vector의 sequence로 바꾸었다. latent sequences의 크기는 \(1024\times1024\) 로 이를 길이가 1024인 1024개의 token처럼 transformer의 입력으로 사용했다. 각 token은 MLP weight matrices의 각 row와 일치한다. Shap-E의 모델은 Point-E base 모델과 유사한 부분이 많다.(context length와 width가 동일) 하지만 더 고차원의 샘플(samples in higher-dimensional)을 생성하는데 이는 입출력 채널의 복잡도(dimension)가 증가하였기 때문이다.

Point-E의 conditioning 방식을 동일하게 사용하였다. 이미지 조건부 3d 생성시 256-token CLIP embedding sequence를 transformer context로 사용했으며, 텍스트 조건부 3d 생성시 single token을 사용했다.

Point-E와의 차이점으로는 diffusion model의 출력을 \(\epsilon\) prediction으로 parameterize하지 않았다는 것이다. 대신 본 논문에서는 곧바로 sample을 예측하는 방식을 사용했다. 대수적으로는 동일한 의미이나 초기 실험에서 더 일관된 결과물을 생성하여 해당 방식을 사용하였다고 함.

4.3 Dataset

공정한 비교를 위해 대부분의 실험에서 Point-E와 동일한 3D assets을 사용했다. 하지만 post-processing부분에서는 차이가 있다.

• point cloud 계산시, 20개가 아닌 60개의 view를 rendering했다. 20개만 사용했을때 주어진 view에서 확인할 수 없는 영역때문에 crack 발생 (+NeRF 때문으로 추정)

• point cloud를 4K 가아닌 16K의 point로 만들었다.

• encoder학습을 위한 view를 렌더링 할때 단순한 소재와 라이팅을 사용하였다. 특히 모든 모델은 동일한 고정된 라이팅 조건내에서 렌더링 되었다. ambient와 diffuse shading만 사용 (+반사광이 고려되지 않아 표면이 매끈한 물체는 생성하기 어려울 것으로 추정됨)

  

  Fig. 684 Phong model
  기본적인 shading방식으로 본 논문에서는 specular를 사용하지 않았다
  source - Realistic_Visualisation_of_Endoscopic_Surgery_in_a_Virtual_Training_Environment

text 조건부 모델과 해당 Point-E baseline을 위해 데이터 셋을 더욱 확장했다. 이 데이터 셋을 위해 대략 100만개의 3D assets과 12만개의 (human labeled)caption을 추가로 수집했다.

5. Result

5.1 Encoder Evaluation

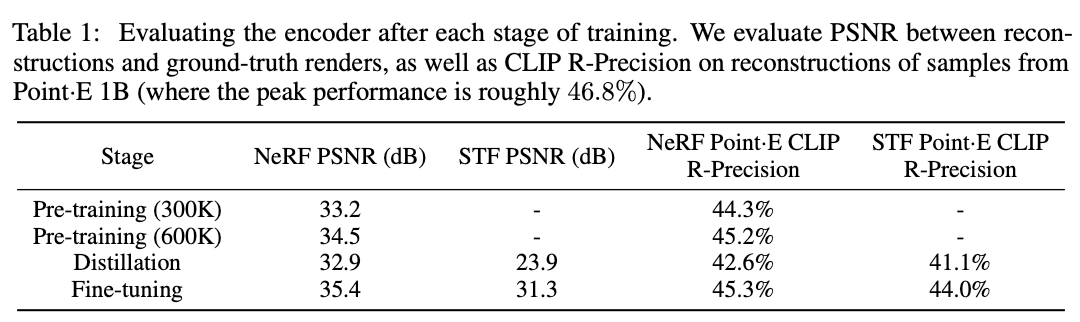
Fig. 685 각 스테이지 별 훈련 이후 encoder 성능평가

distillation에서 rendering 이미지의 퀄리티가 떨어지는 것처럼 보이나 finetuning시 퀄리티가 더욱 좋아진다. 또한 STF의 퀄리티 또한 크게 상승한다.

5.2 Comparison to Point-E

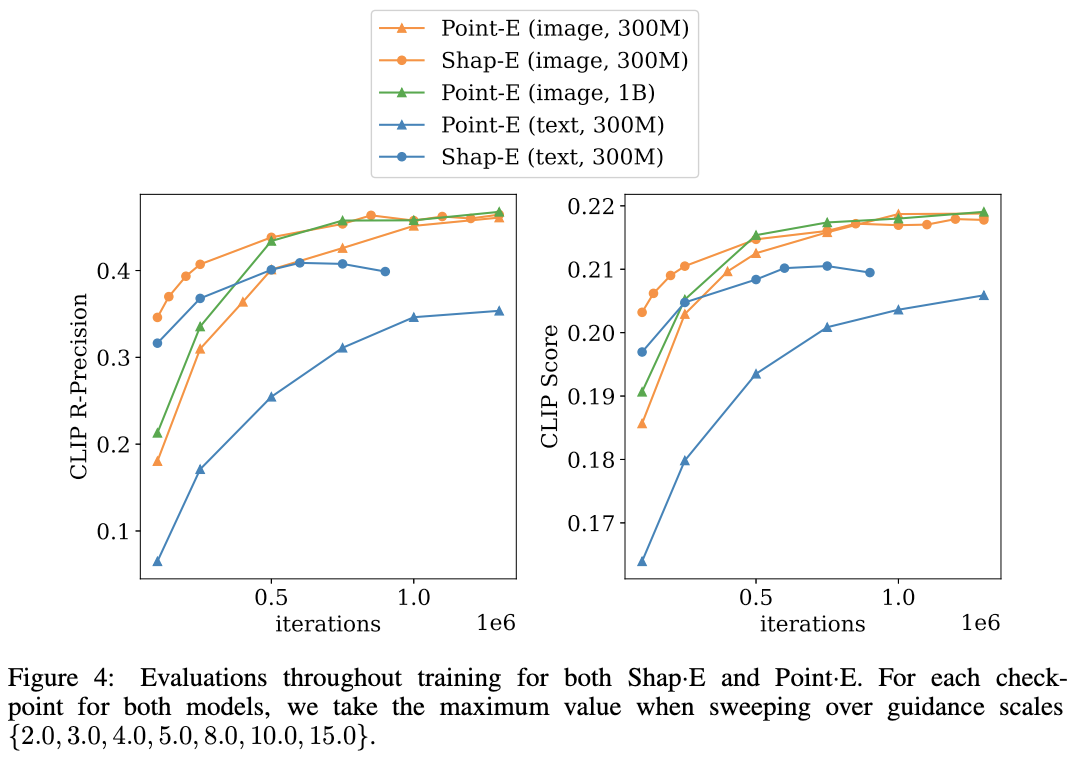
Fig. 686 Shap-E와 Point-E비교
세모 마크가 Point-E, 원형 마크가 Shap-E이다.

point-E보다 Shap-E의 CLIP score가 더 높다. 더 많은수의 parameter를 가진 point-E를 사용하여도 Shap-E의 성능이 우수함.

두 평가 지표 모두 OpenAI의 CLIP (Contrastive Language-Image Pretraining) 모델을 활용한 평가 지표로 CLIP score의 경우 주어진 텍스트와 생성결과의 일관성을 평가하기 위한 것이고, CLIP R precision의 경우 생성결과와 참조 이미지가 얼마나 비슷한지 평가하기 위한 것이다.

Fig. 687 Shap-E와 Point-E비교

동일한 base model의 크기 동일한 데이터셋으로 학습시킨 결과. 텍스트 조건부 생성시에는 퀄리티 차이가 크지 않음.

Fig. 688 Shap-E와 Point-E비교

이미지 조건부 생성시에는 비교적 차이가 크다. 벤치 결과를 보면 point-E에서 나무사이 빈공간을 무시해버린것을 볼수 있다. 위의 강아지와 컵 이미지 기반 생성 결과를 보면 point-E와 shap-E가 유사한 케이스에서 실패하는 모습을 보였다.

5.3 Comparison to Other Methods

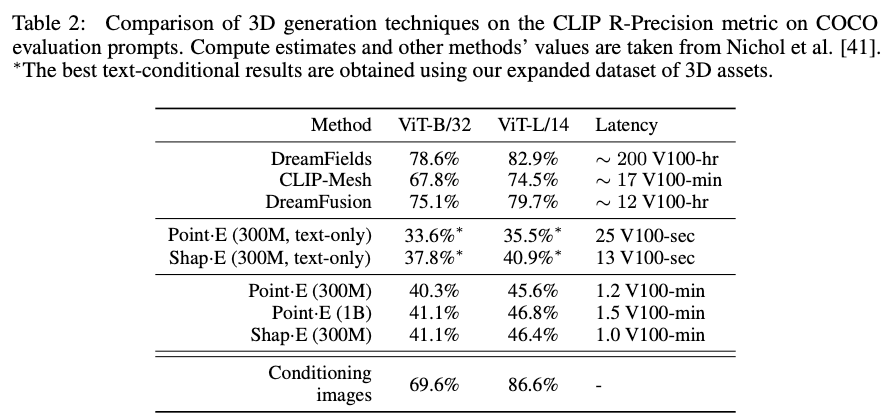
Fig. 689 COCO 데이터셋을 이용한 비교결과

reference latency에서 point-E와 Shap-E의 차이가 있는데, 이는 Shap-E는 추가적인 upsampling diffusion model을 사용하지 않기 때문이다.

6. Limitations and Future Work

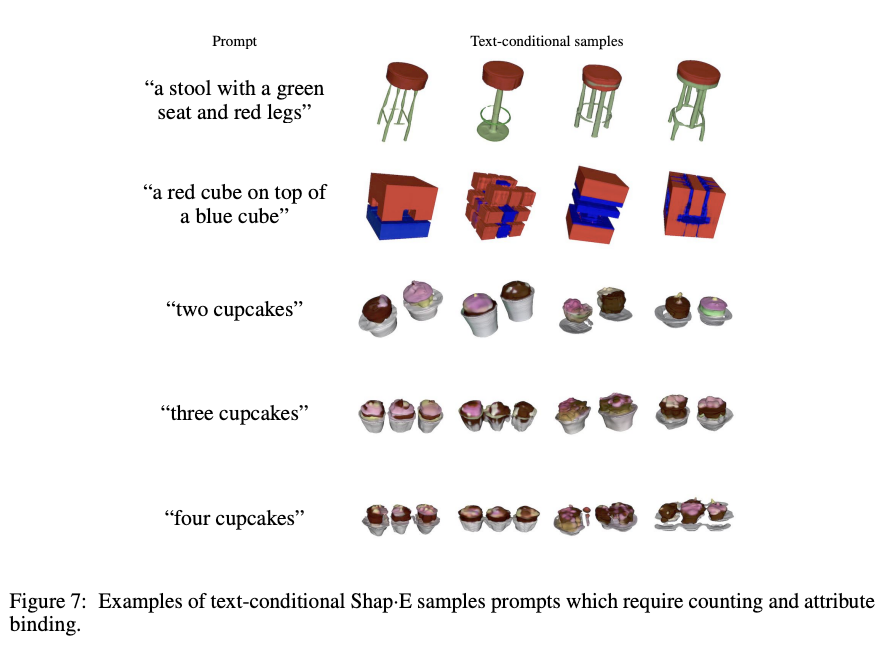
Fig. 690 텍스트 조건부 생성 결과

왼쪽 그림과 같이 여러가지 특성을 가진물체를 생성하는데에 어려움을 겪는 모습을 보인다. 이는 학습에 사용한 paired data가 제한적이기 때문으로 더 많은 3D dataset을 수집하면 나아질 수 있다. 또한 texture의 세부 특성을 encoder가 무시하는 경우도 있는데, 더 나은 encoder를 사용함으로써 개선될수 있다.

Shap-E는 다양한 3D 생성 기술들을 융합하는데에 도움을 줄 수 있다. 예를 들어 Shap-E로 생성한 NeRF와 mesh를 다른 최적화 기반 모델을 초기화 하는데 사용하는 것이다. 이를 통해 더 빠른 수렴도 가능할 것으로 생각된다.

7. Conclusion

Shap-E는 latent diffusion model을 3D implicit function공간에서 전개하여 NeRF와 textured mesh 모두를 생성 할 수 있었다. 동일한 데이터셋을 활용하여 다른 생성모델들과 비교하였을때 더 나은 성능을 보임을 확인했다. 또한 text 조건부 생성시 이미지 없이도 다양한 흥미로운 물체를 생성할 수 있음확인했다. 이는 implicit represention을 생성함에 큰 가능성을 보여준다.

8. Acknowledgements

특정 인물들에 대한 언급 외에도 ChatGPT로 부터 valuable writing feedback을 받았다고 표현한 부분있었다.