A Study on the Evaluation of Generative Models

A Study on the Evaluation of Generative Models#

학습 자료#

A Study on the Evaluation of Generative Models

https://arxiv.org/pdf/2206.10935.pdf

0. Abstract#

  • GAN, Diffusion등 생성 모델의 놀라운 발전이 이어지고있다.

  • 다만 이러한 생성모델을 평가하는 척도(metric)의 선정은 아직 어려운 문제로 남아있다.

  • 그나마 Inception Score(IS)나, FID Score를 통해 모델을 평가하고있지만 이 metric들도 완전하지 않음

  • 이 논문을 통해

    • 생성 평가의 지표에 대해 한번더 고찰하고

    • 현존하는 Metric에 대한 방향을 제시

1. Introduction#

  • 최근 GAN, Diffusion 등 Implicit generative model들이 뛰어난 성능을 보여줌

  • 하지만 다른 task(classification, segmentation 등)와는 다르게 생성 모델의 metric을 정하는것은 challenging ( classification ; P&R, F1 score / segmentation ; IOU(Intersection Over Union)

  • 그나마 이미지의 featue map이나 classfier score를 사용하는 FiD, Inception score가 잘 쓰이는 추세

  • 위 metric의 단점

    1. real 이미지 분포의 space에서 해당 수치가 정말 유의미한 연관이 있는지 증명되지 않음

    2. pretrained model의 거대한 train set이 specific 이미지의 feature에 얼마나 좋은 성능을 미치는지 알수 없음(inception net ; imagenet / ddpm ; face)

  • Human study의 직관적인 방식도 있지만 time과 cost를 매우 필요로한다는 점과 model의 Diversity는 측정하기 어렵다는 단점

    • e.g ) 하나의 좋은 이미지만 생성해도 좋은 score를 받을 수 있음

  • 이 논문에서는

    1. Image-GPT 모델을 통해 high quality의 new synthetic dataset을 생성

    2. 여러 모델을 위의 데이터로 학습하고 FiD, IS등 다양한 metric을 측정

    3. 이를 실제 KL Divergence, Reverse KL Divergence 값과 비교해서 metric의 유효성을 검증

    4. FID, IS등 다양한 metric의 base model로 쓰이는 Inception-V3과 CLIP 의 비교를 통해 Inception-V3 모델의 적합성을 검증

2. BackGround#

2.1. KL-Divergence(Kullback-Leibler divergence)#

  • 두 확률분포의 유사도를 측정하는 지표

\[ KL(P || Q) = \sum_{x} P(x) \log\left(\frac{P(x)}{Q(x)}\right) \]

  • 특징

    • lower is better

    • KL ≥ 0, (KL(p, q) = 0, if p ==q)

    • KL(p, q) ≠ KL(q, p) // not symmetric

    • Reverse Kullback-Leibler Divergence(RKL) = KL(q, p)

    • 대부분 P가 True distribution, Q가 estimated distribution

2.2. Inception Score(IS)#

  • 생성된 이미지의 Fidelity와 Diversity를 측정

    • fidelity : 특정 Label의 이미지를 얼마나 잘 예측하는지

    • diversity : 다양한 class의 이미지들을 얼마나 고르게 생성해내는지

      A_Study_on_the_Evaluation_of_Generative_Models_01

      Fig. 36 Image 1#

\[ \text{IS}(G) = \exp\left(\mathbb{E}_x \left[D_{\text{KL}}(P(y|x) \, || \, P(y))\right]\right) \]

  • 특징

    • \(P(y|x)\) ; 모델의 Fidelity, \(P(y)\); 모델의 Diversity

    • higher is better

2.3. FiD(Fréchet Inception Distance)#

  • real 이미지와 generated 이미지의 Feature vector를 추출 후 평균과 공분산을 통해 계산(Frechet distance)하는 평가지표

\[ FID = \lVert \mu_x - \mu_g \rVert^2 + \text{Tr}(\Sigma_x + \Sigma_g - 2(\Sigma_x\Sigma_g)^{1/2}) \]

  • 특징

    • Inception-V3의 마지막 pooling layer의 feature map을 사용

    • Lower is better

    • \(\mu_x - \mu_g\); 이미지의 Quality를 측정

    • \(\text{Tr}(\Sigma_x + \Sigma_g - 2(\Sigma_x\Sigma_g)^{1/2}\); 모델의 Diversity를 측정

2.4. Kernel Inception Distance#

  • FiD에서 Frechet distance를 사용하는 대신 kernel trick을 사용해 확률 분포의 유사도를 계산

  • 특징

    • 적은 데이터셋의 평가에 효과적임

    • FiD metric보다 속도가 오래걸림 (FiD : O(n), KiD : O(n^2))

2.5. FID∞ & IS∞#

  • 해당 논문에서 FiD와 IS metric에 bias가 있음을 증명하고 dataset의 sampling 기법을 변경(gaussian random sampling → sobol sequence sampling)하여 unbiased 한 metric을 제안

    A_Study_on_the_Evaluation_of_Generative_Models_02

    Fig. 37 Image 2#

2.5. Clean FiD#

  • Inception-v3에 이미지를 통과하기위해 image resize 과정이 포함되는데 이는 score값에 영향을 줄수 있어 best percformance의 metric을 측정하기 위한 all in one process를 제안

3. Synthetic dataset as a benchmark#

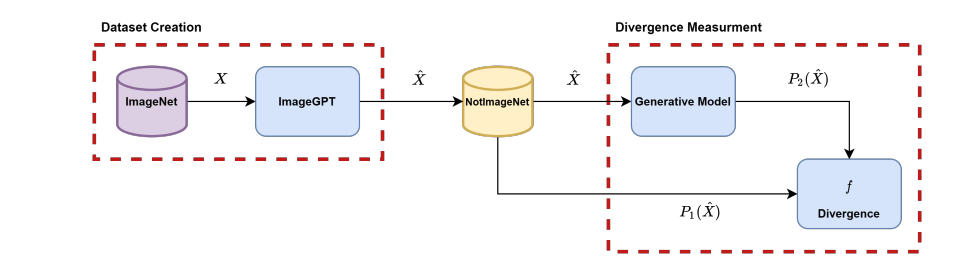
A_Study_on_the_Evaluation_of_Generative_Models_03

Fig. 38 Image 3#

  • imagenet의 데이터를 ImageGPT를 통해 재생성(a.k.a. NotImageNet)

    • imageGPT

      • vision 분야에 transformer(in gpt-2)를 사용 + labeling dataset이 필요없는 자기지도 학습 방식

        A_Study_on_the_Evaluation_of_Generative_Models_04

        Fig. 39 Image 4#

      • imagenet challenge에서도 상당한 score를 보임

  • 이를 생성모델에 통과한 \(P_{2}(\hat{x})\)과 \(P_{1}(\hat{x})\) 두 분포를 비교

  • 한계

    • explicit model에만 적용 가능하고 implicit model에는 적용할 수 없음

    • explicit model : 생성되는 데이터의 분포를 명시적으로 모델링하여 학습하고 주로 Gaussian Noise로부터 이미지를 생성 (VAE …)

    • implicit model : 데이터의 생성 과정에 대해 학습하고 주로 주어진 데이터 분포로부터 샘플링하여 학습 (GAN …)

4. Comparison between evaluation metrics#

4.1. Volatility

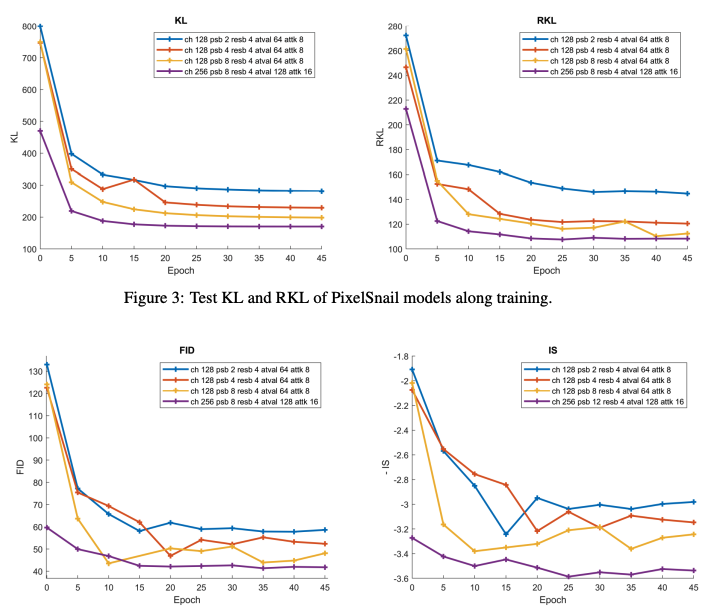
A_Study_on_the_Evaluation_of_Generative_Models_05

Fig. 40 Image 5#

  • KL, RKL은 적은 양의 Epoch(15-20) 후에 바로 수렴하는 방면 FID와 IS는 큰 변동성을 보임

  • 모델의 Capacity가 증가할수록 KL과 RKL의 수치가 개선되는 것을 확인

  • FID나 IS가 KL, RKL의 그래프와 매우 다른 형태를 띄는것을 확인(특히 IS)

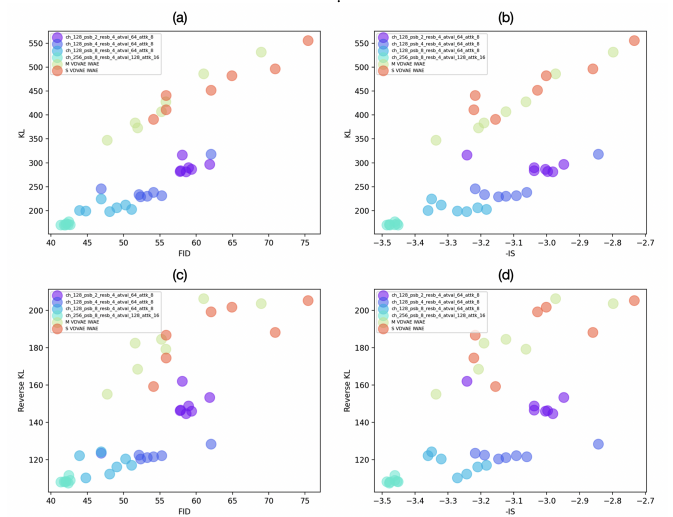
A_Study_on_the_Evaluation_of_Generative_Models_06

Fig. 41 Image 6#

  • FID나 (negative)IS가 KL과는 높은 colleration을 보이지만 RKL과는 높지 않은 colleration을 보인다.

  • 모델의 Capacity에 따라 KL, RKL의 수치 변화는 크지 않은 데 반해 FID나 IS는 굉장히 큰 수치의 변화를 보여준다.

4.1. Ranking Colleration

  • 여러 모델에 대해 metric 별로 순위를 매겨 순위의 유사도를 비교

  • Kendall’s τ

    • ranking이 매겨진 수열 사이의 유사도를 측정

    from scipy import stats
>>> h = [1, 2, 3, 4, 5]
>>> w = [1, 2, 3, 4, 5]
>>> z = [3, 4, 1, 2, 5]
>>> stats.kendalltau(h, w)
SignificanceResult(statistic=0.9999999999999999, pvalue=0.016666666666666666)
>>> stats.kendalltau(h, w)
SignificanceResult(statistic=0.19999999999999998, pvalue=0.8166666666666667)

  • Result

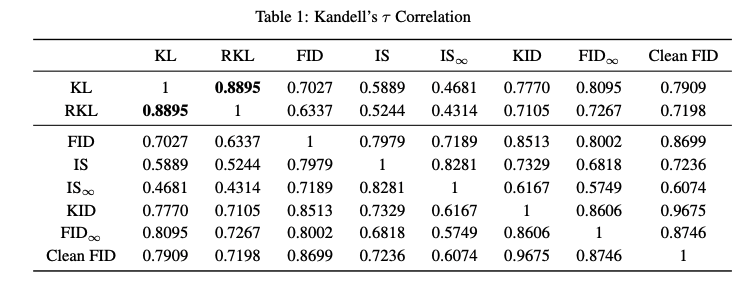
    A_Study_on_the_Evaluation_of_Generative_Models_07

    Fig. 42 Image 7#

    • KL - RKL의 유사도는 매우 높음(0.889)

    • KL과의 유사도를 비교해보면 FID infinity > FID > IS

    • CleanFID-KID(0.96)을 제외한 나머지 metric간 유사도는 굉장히 낮음

    • Inception network 기반의 metric 중에서는 FID infinity이 가장 높고, IS와 IS infinity score가 가장 낮음

5. Is Inception all we need?#

  • FID, Inception Score 등 대부분의 metric이 이미지의 feature 혹은 score 측정을 위해 inception-v3를 사용하는데 과연 적절한가?

  • 가정

    • FID, FID infinity는 feature space가 gaussian distribution을 따른다는 가정하에 측정되는 score

  • 실험

    1. 따라서 생성 모델을 통해 10K의 이미지를 생성하고

    2. 원본의 20K의 이미지를 sampling

    3. 각각의 이미지를 Inception network와 CLIP network를 통해 feature vector를 추출

    4. Gaussian model에 feature vector를 fitting

    5. 이때 gaussian model을 기반으로 각 샘플의 확률값을 계산한다.

  • 결과

    A_Study_on_the_Evaluation_of_Generative_Models_08

    Fig. 43 Image 8#

    • 확률 값이 낮은 tail 부분의 feature vector의 원본 이미지들을 퀄리티가 낮아야함

    • 실제로 tail 부분의 확률을 갖는 이미지들을 확인해보면 CLIP을 보면 확실히 퀄리티가 떨어지는 반면 Inception의 이미지들은 좋은 퀄리티를 보이고 있음 → Gaussian 분포의 가정에 위배

5.2 Normality test for latent representation

  • 위의 feature vector들을 1 Dimension에 투영시켜 normal distribution을 따르는 지 확인한다.

  • 실험

    1. Inception, CLIP을 통해 feature vector를 추출한다.

    2. linear transformation 연산을 통해 각각 1-D로 투영시킨다.

    3. 각각의 p-value를 구한다.

      1. p-value : 어떠한 사건이 우연히 일어날 확률

      2. if p-value < 0.05 ; 우연히 발생할 확률이 거의 없다. 인과관계가 있다.

      3. if p-value > 0.05 ; 우연히 발생할 확률이 크다. 인과관계가 없다.

      4. gaussian normal distribution은 random을 기반으로하기때문에 인과관계가 작아야한다. 즉, p-value가 커야한다.

  • 결과

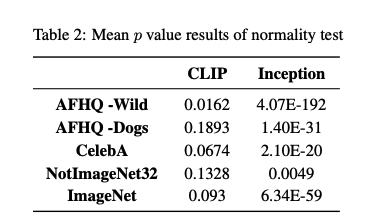
    A_Study_on_the_Evaluation_of_Generative_Models_09

    Fig. 44 Image 9#

    • 모든 test dataset에 대해 CLIP의 p-value값은 0.05를 넘어 random성을 유지하지만, Inception은 0.05보다 낮은 값을 보여 random성을 유지하지 못한다.

    • 따라서, Inception net을 통한 metric 측정보다 CLIP을 통한 metric 측정을 제안한다.

Contents