Information
Title: One-Step Image Diffusion with Distribution Matching Distillation
Reference
Code: tianweiy/DMD2
Author: Joongwon Lee
Last updated on Oct. 16, 2024
One-step Diffusion with Distribution Matching Distillation#
Introduction and Preliminaries#
Overview#
Diffusion model has revolutionized image generation, 하지만 느린 sampling speed 가 느린 문제점이 있음
Accelerating sampling speed 를 목적으로 하는 많은 연구가 이루어져 왔음
ODE solving: diffusion model 의 큰 틀은 유지한 채 sampling step 의 수를 줄이면서 유사한 수준의 sample 생성 (DDIM, InstaFlow, CFM)
하지만 여전히 50 ~ 100 step 이하로 step 을 줄이게 되면 sample quality 가 크게 감소하여 diffusion distillation 을 통한 one-step generation 방법이 연구되어지고 있음
Single step distillation: Diffusion model 을 teacher 삼아 one-step generation model 학습
직관적으로 생각해보면, diffusion model 을 학습 시킨후 학습된 모델을 통해 다수의 (noise, image) pair 얻은 후 one-step VAE 를 학습시키는 것을 생각 해 볼 수 있음.
그러나, 학습된 multi step 으로 학습 된 diffusion model 을 one-step generation model 에 distillation 을 하는 것은 어려움이 있음
Noise level 을 점진적으로 증가 시키며, one-step generation 을 학습시키는 방법
GAN 에서 영감을 받아, (noise, image) 의 대응을 강제하는 대신 (such as autoencoder), student model 이 생성하는 이미지를 teacher model (original diffusion model) 이 생성하는 이미지와 indistinguishable 하게 학습시키는 distribution matching 전략을 생각해 볼 수 있음
Diffusion model 의 score (\(\newcommand{\laplacianx}{\Delta x}\)\(\nabla_{\mathbf{x}} \log p(\mathbf{x})\)) 을 사용해서 student model (\(p(x)\)) 을 학습시킬 수 있음 (real image score 가 증가하는 방향으로 pattern 을 업데이트 하는 것이 desired 방향 + fake image 를 생성하는 diffusion model 의 score 을 감소시키는 방향으로 parameter update)
Diffusion model and score base model
엄밀하게 본다면, 이 논문은 diffusion model (DDPM style) 보다는 score matching 의 철학과 논리전개를 바탕으로 두고 있음. 그러나, diffusion model 과 score based model 은 궁극적으로 같은 objective 를 다른 방식으로 학습하고 있을 뿐이고, 그 score 과 diffusion model 이 예측하는 one-step denoised 분포 (\(\mu_{base}\)) 는 쉽게 변환 가능함.
\[ s_{\text{real}}(x_t, t) = - \frac{x_t - \alpha_t \mu_{\text{base}}(x_t, t)}{\sigma_t^2} \]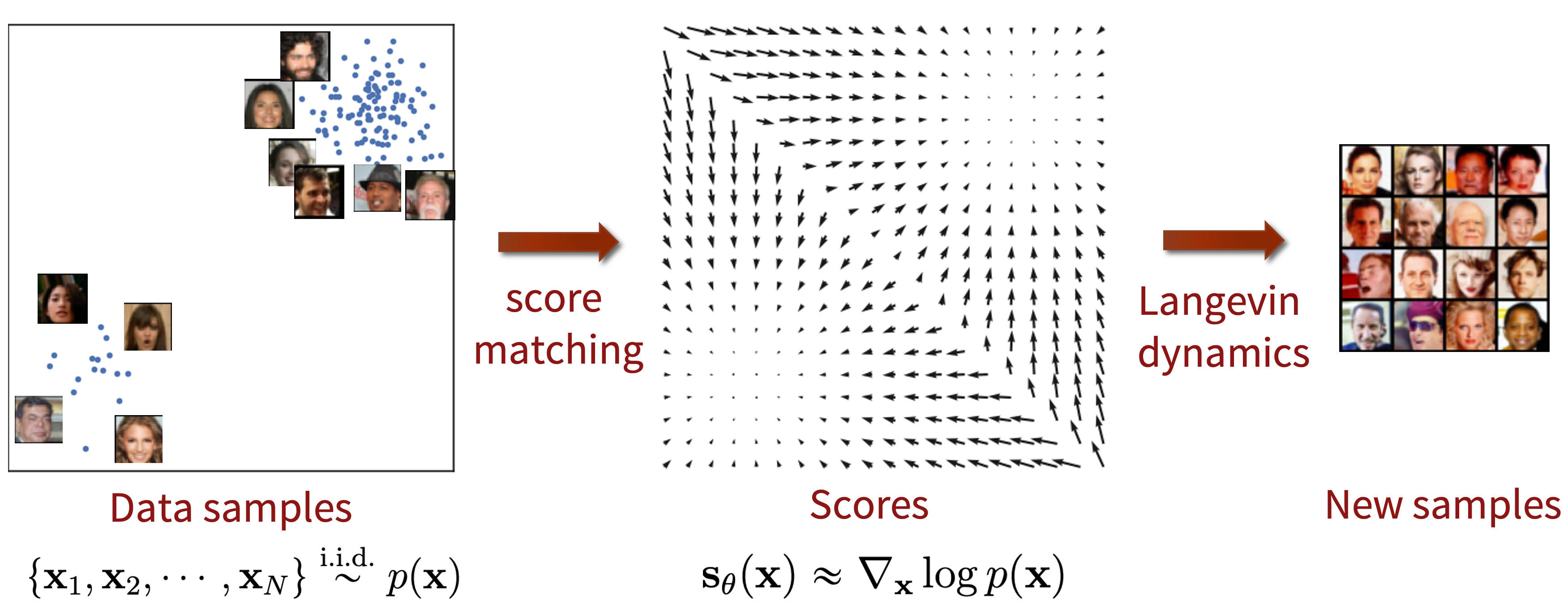
Fig. 577 NCSN#

Fig. 578 Langevin sampling of score models#
Method#
Overview#
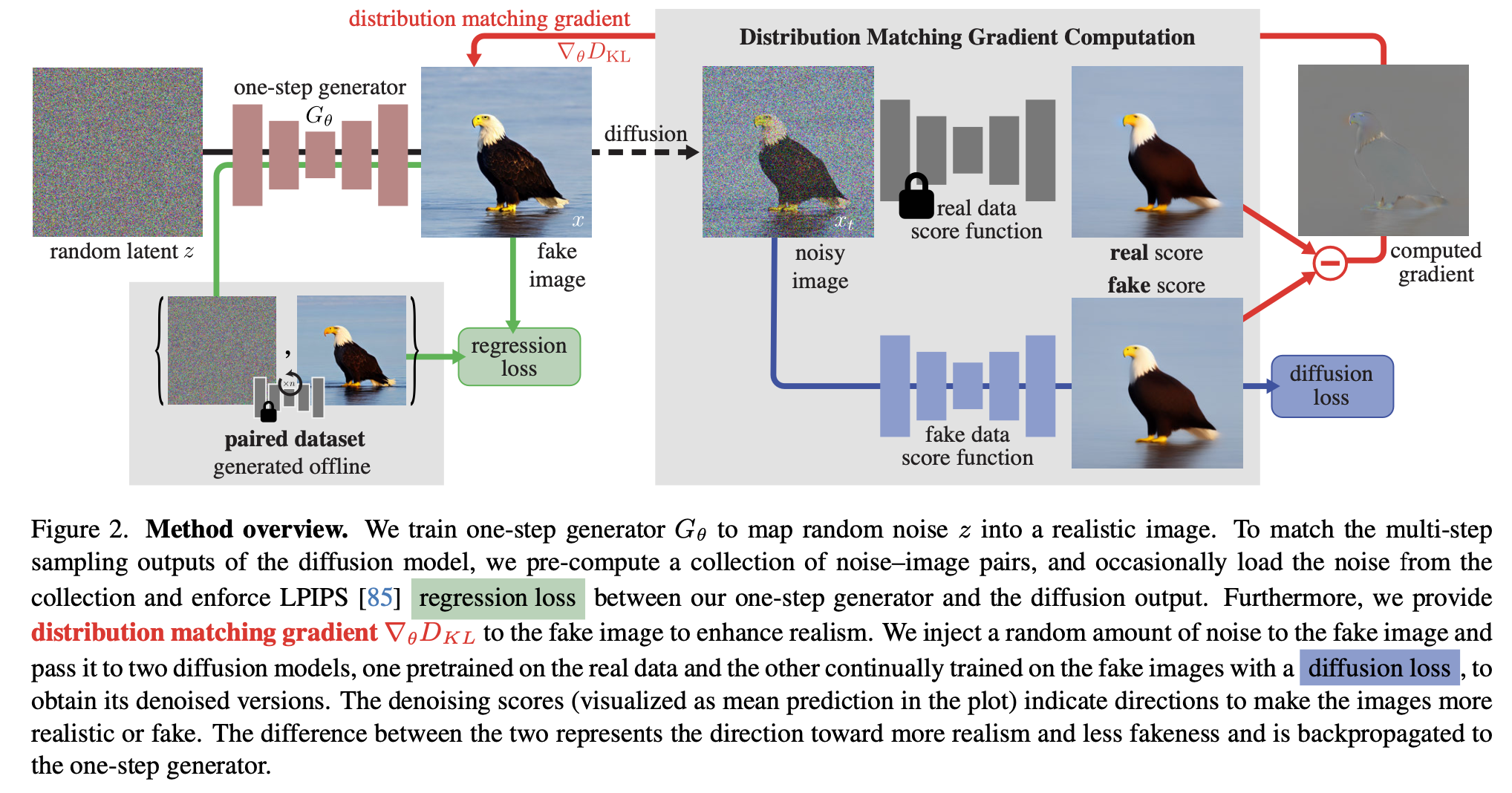
Fig. 579 Overall scheme#
학습된 diffusion model (real data score function) 이 주어진 상황에서 one-step generator (\(G_{\theta}\)) 를 학습시키기 위해, 두개의 loss 1) distribution matching gradient (엄밀하게는 loss 보다는 parameter update gradient) 2) regression loss 를 사용
Adversarial AutoEncoder 가 연상되는 architecture 를 가지고 있음
Adversarial AutoEncoder
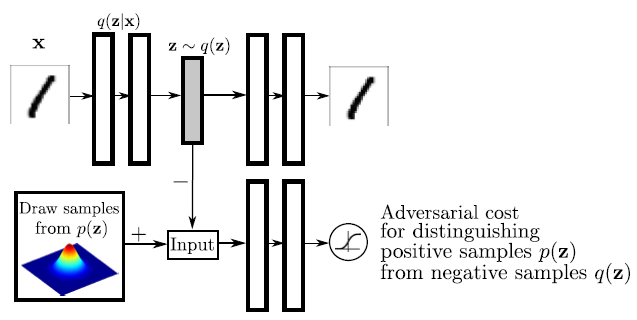
Fig. 580 Adeverserial AE architecture#
AAE 는 VAE 가 생성하는 이미지에 대한 1) regression loss 와 2) implicit distribution matching loss 를 가지고 있는데, 여기서 implicit distribution matching 을 teacher diffusion model 의 distribution matching gradient 로 대체한 형태
총 네 부분으로 나뉘어져 있음
Paired dataset construction
Pretrained base model (= real data score function, freezed)
One-step generator (main objective)
Fake data generator (= fake data score function, on-line training)
Distribution Matching Loss#
우선, 생성모델의 training objective를 생각해보면, \(p_\text{fake}\) (one-step generator이 생성하는 분포) \(p_\text{real}\) (실제 데이터의 분포) 를 matching 시키도록 학습을 시켜야하는 것이 one-step generator의 학습 objective이고 아래와 같이 씌여질 수 있음:
지만, \(p_\text{real}(x)\) 를 바로 구하는 것이 어려움 (이것이 곧 생성모델의 objective). 그러나, 모델을 학습시키기 위해서는 \(D_{KL}\) 을 직접 구할 필요는 없고, \(D_{KL}\) 을 minimize 하는 (fake 과 real 의 분포사이의 거리를 최소화 시키는 방향으로) parameter update 를 하기 위한 미분값만 알면 충분함. 위 식을 one-step generator 의 learnable paramter (\(\theta\)) 에 대해 미분 해주면,
이 유도되는데, 여기서 score \(s_{\text{real}}(x)\) 와 \(s_{\text{fake}}(x)\) 를 정확히 알 수 있다면, one-step generator 을 학습시킬 수 있음. 단, score 이 \(x\) 가 존재하는 전체 space 에 대해서 잘 작동하는 score 이여야함 (= Score-SDE).
이제, 그러면 우리의 objective 는 real score 와 fake score 을 어떻게 구할지가 되는데, \(s_{\text{real}}(x)\) 은 pretrained diffusion model 에서:
와 같이 유도됨. \(s_{\text{fake}}(x)\) 의 경우가 복잡해지는데, \(s_{\text{fake}}(x)\) 는 one-step generator 가 생성하는 이미지의 score function 라서 one-step generator 로 생성 된 이미지가 있어야 해당 이미지를 생성하는 diffusion 모델을 학습시켜서 구할 수 있음.
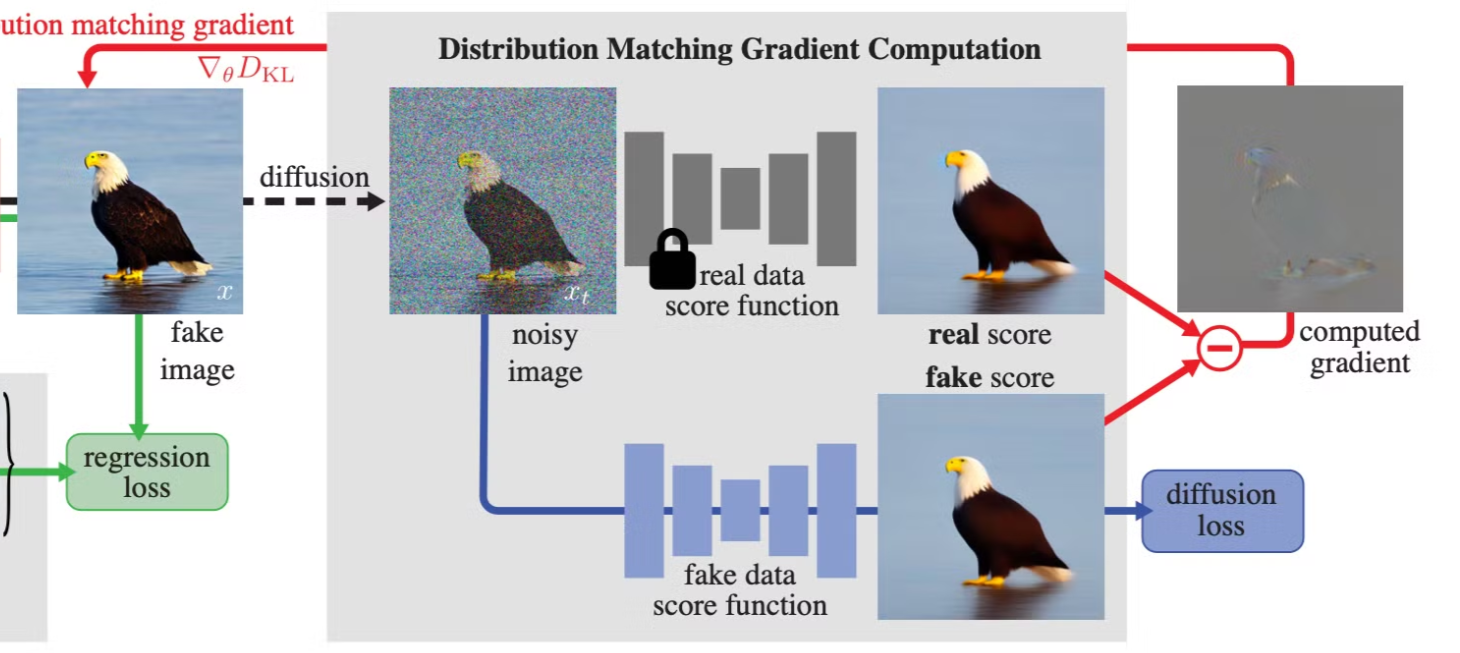
Fig. 581 Distribution matching gradient computation#
여기서 저자들은 fake data score function (initialized to real data score function) 을 동시에 학습시키는 방법으로 해결
정리하자면, real score 은 real distribution (data distribution) 방향으로 parameter update를 하면서 fake distribution (one-step generation 의 output) 을 real distribution 에 가깝게 일치시키는 역할을 하며, fake score 의 반대방향으로 parameter update 를 하는 것은 fake data generator (one-step generator) 의 반대방향으로 distribution 을 밀어내서 most probable 한 한개의 점으로 모든 fake image 가 collapse 하는것을 방지하는 regularizer 역할을 한다.
Regression Loss#
그런데, score 만을 사용하여 one-step generator 을 학습시키는 것은 충분하지 않음. 두가지 측면에서 생각 해 볼 수 있는데 1) Practically, 매우 작은 noise level 에서는 score 이 reliable 하지 않아짐 2) Theoretically, \(\nabla_x \log p_(x)\) 는 \(p(x)\) 의 scale 에 영향을 받지 않아, 데이터의 높고 낮음에 대한 정보를 줄 수 없음.
따라서, real + fake score 로 학습이 진행된다면, 낮은 real score 을 보이는 영역은 커버하지 못하는 부분으로 one-step generation 모델이 수렴하게 될 것 이고, high dimension 에서는 generated image 의 pixel level accuracy 에 문제가 생길 수 있음.
여기서 저자들은 pixel-wise MSE (regression loss) 를 사용하여 간단히 이 문제를 해결함.
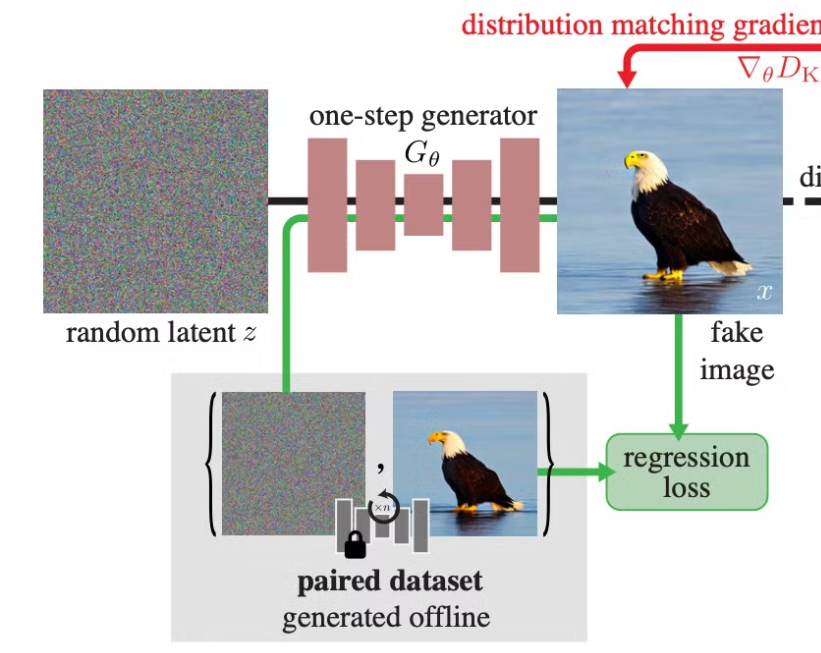
Fig. 582 Regression loss#
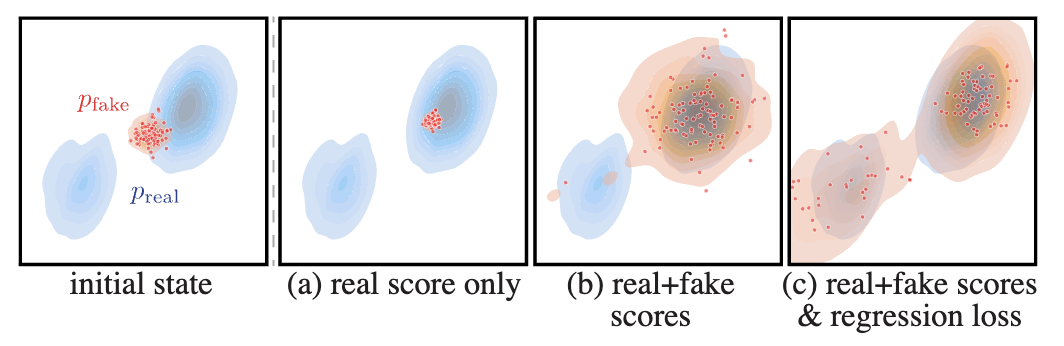
Fig. 583 The effect of real and fake scores and regression loss#
그렇다면, Regression loss 하나만으로는 학습이 왜 불가능한가? (개인적 생각)
이론상 regression loss 만을 사용해도 충분히 one-step generator 을 학습시킬 수 있어 보인다. 그러나, regression 의 근본적 문제점은 distribution to distribution matching 이 아니라는 점이다. e.g.
Regression loss 를 얻기 위해서는 (noise, real image) pair 가 필요하게 되는데, 저자들은 학습된 diffusion model 에서부터 ODE solver 을 사용하여 gaussian noise와 real image 사이에 쌍을 얻어서 데이터셋을 학습 이전에 구축, 해당 pair들을 바탕으로 regression loss 를 구함 (Learned Perceptual Image Patch Similarity).
Full algorithm#

Fig. 584 Training algorithm#
Results#
Main comparison#
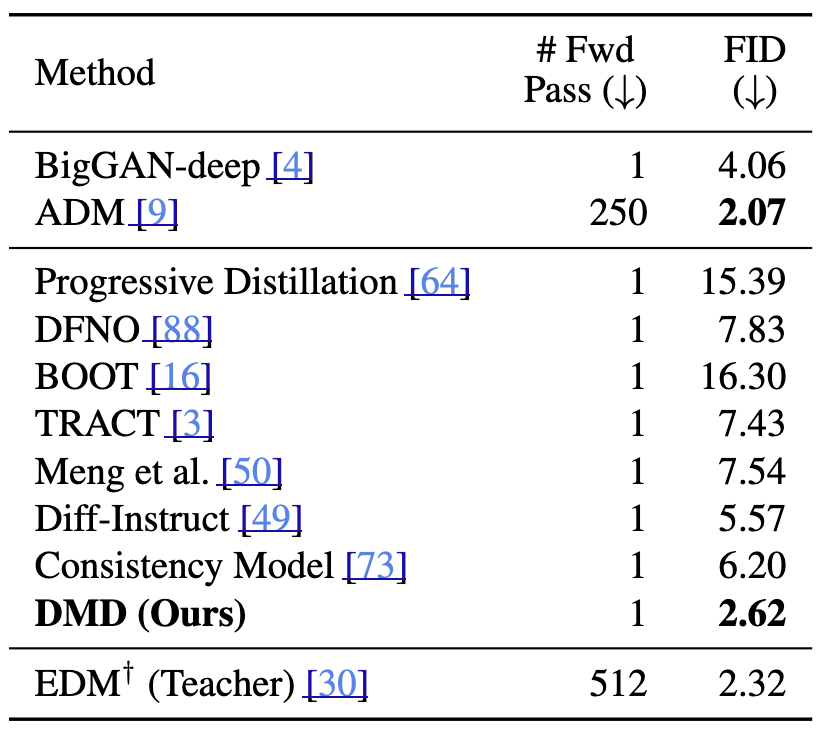
Fig. 585 Image generation benchmarks#
Ablation Study#

Fig. 586 Ablation on distribution matching#

Fig. 587 Ablation on regression loss#
Comparison with Unaccelerated Models#
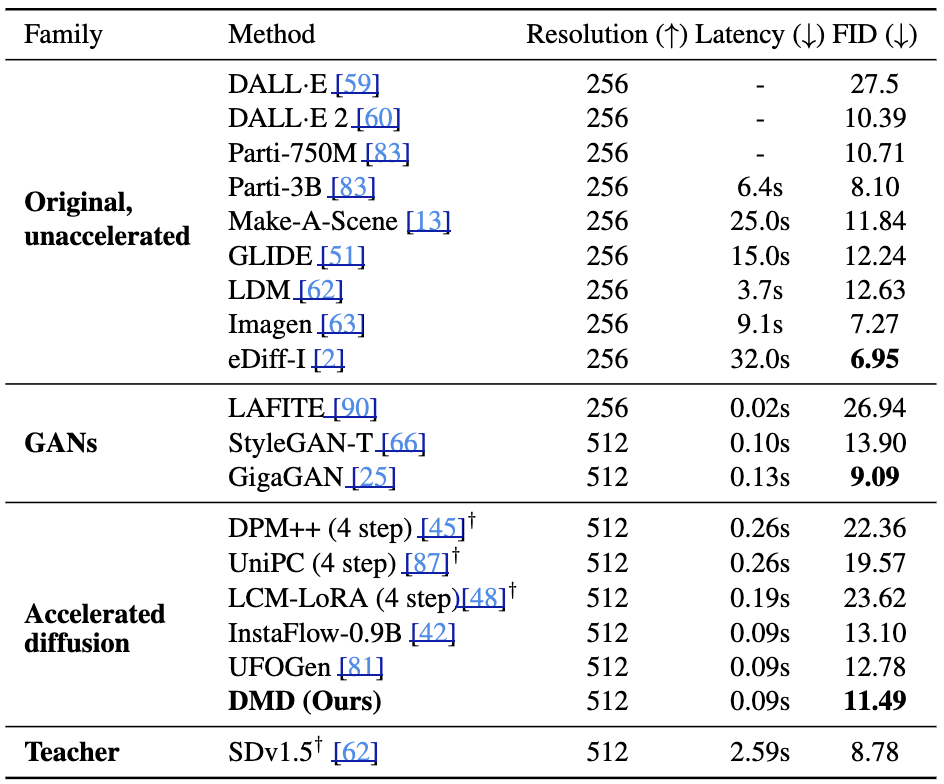
Fig. 588 Comparison with Unaccelerated Models#
Conclusion and Limitations#
Score model 을 사용한 distribution matching loss 와 regularizing term 인 regression loss 를 통해, teacher model 에 준하는 성능을 낼 수 있었다
One step generator 와 multi-step generation 사이에는 근본적인 성능 tradeoff 가 존재함
one-step generator 의 성능은 teacher diffusion model 의 성능에 종속된다
