LCM-LoRA: A Universal Stable-Diffusion Acceleration Module

Information

LCM-LoRA: A Universal Stable-Diffusion Acceleration Module#

Proposal#

  • Latent Consistency Models(LCMs)에 Low Rank Adaptation (LoRA)을 적용하였다.

  • LoRA를 이용하여 Stable Diffusion에 대한 추가적인 학습 없이도 fine-tuning 가능. (Accelerate 효과 극대화)

  • 이전의 다양한 PF-ODE (Probability-Flow ODE) solver를 사용한 방법론들보다 더 generalized 된 성능

1. Introduction#

기존 연구의 한계점#

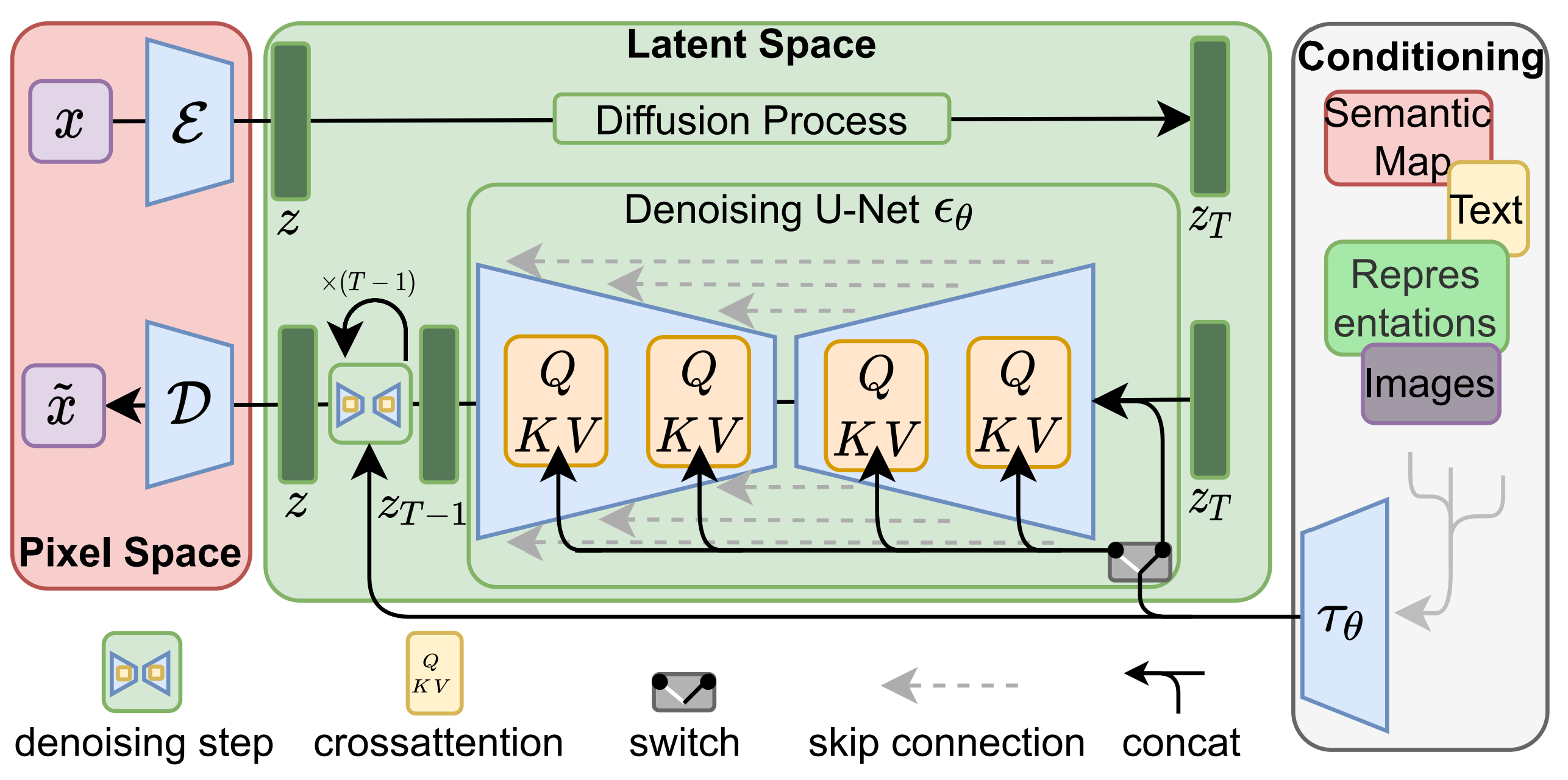
Latent Diffusion Models(LDMs)은 image generation 분야에서 좋은 성능을 보이고 있다. 그러나 아직까지는 느린 reverse process 때문에 사용자가 직접 사용하기에는 무리가 있다. 따라서 LDMs을 가속화(Accelerate)하기 위한 기법들이 제안되어 왔는데 크게 2가지로 나눌 수 있다:

  1. DDIM, DPM-Solver, DPM-Solver++ 등 ODE-Solver 기반 방법론.

  2. LDM을 경량화 하기 위한 Distillation 기반 방법론.

ODE-Solver 방법론은 sampling step을 줄일 수 있지만 Classifier-free Guidance(CFG) 등을 사용할 때 Computation 적으로 Overhead가 있을 수 있다. Distillation 방법론 또한 Distillation 시 Computation적으로 Overhead가 있어 한계가 있다. ex)Guided Distill : 2 stage의 distillation 방식 + high resolution image 생성 한계

LCMs 기반 연구#

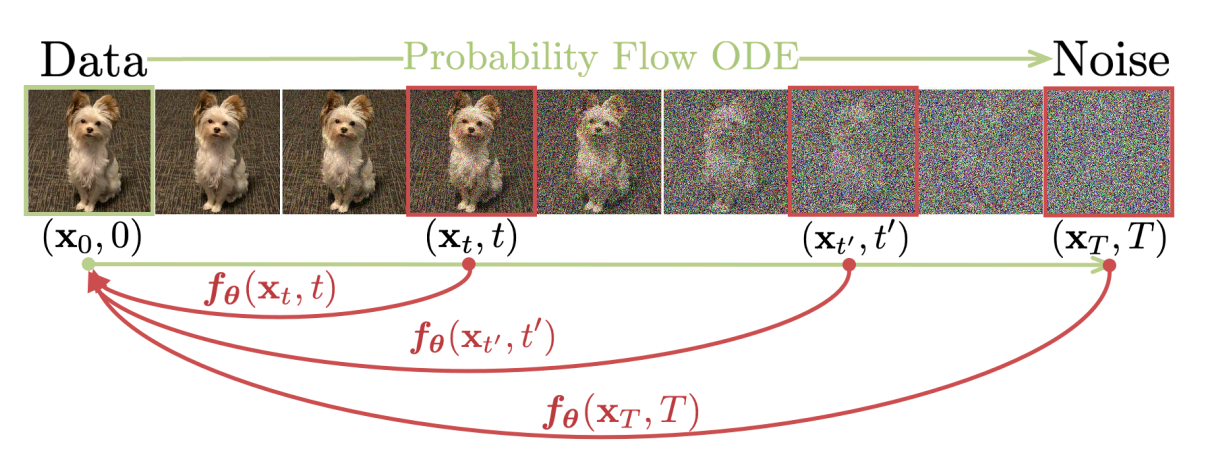
이에 반해 Consistency Models(CMs)에서 영감을 받은 Latent Consistency Models(LCMs)은 매우 좋은 대안이다. backward process를 augmented Probability Flow ODE(PF-ODE) problem으로 접근하여 반복적인 step을 획기적으로 줄일 수 있었다. LCMs은 1~4 step만으로도 높은 퀄리티의 고해상도 이미지를 생성해낼 수 있으며 큰 리소스가 필요하지 않다.

그러나 LCMs을 기반으로 하는 방법론은 새로운 데이터셋에 대해 finetuning이 필요하거나 pretrained LDMs을 필요로 하는 한계가 존재한다.

따라서 본 연구는 추가 학습없이 Stable Diffusion(SD)이나 SD-LoRA 등에 plug-in 해서 사용할 수 있는 LCM-LoRA를 제안한다. LCM-LoRA는 새로운 종류의 neural network 기반 PF-ODE Solver이며, 강력한 일반화 성능을 보여준다.

Parameter-Efficient Fine-Tuning#

Parameter-Efficient Fine-Tuning(PEFT)이란 파라미터를 효율적으로 사용하면서 fine-tuning 할수 있는 연구를 의미한다. Knowledge Distillation, Pruning, Quantization 등이 있다.

본 연구에서는 PERF 기법 중 RoLA를 사용했다.

Low Rank Adaptation#

기존에 pre-trained 된 가중치 \(\Phi_0\)에 대하여 새로운 task에 fine-tuning하는 모델 \(P_\Phi(y|x)\)는 다음과 같이 가중치가 업데이트 된다. (\(\Phi_0+\Delta\Phi\))

\[\underset{\Phi}{max}\sum_{(x,y)\in Z}\sum^{|y|}_{t=1}\log{(P_\Phi(y_t|x,y<t))}\]

LLM이나 Stable Diffusion과 같은 대규모 모델은 새로운 task로 fine-tuning 시 매우 큰 차원의 모델 파라미터를 다시 학습하기 때문에 매우 큰 Cost가 생긴다. (시간적, 자원적) 이때 weight의 차원은 줄이면서 변화량을 기록하는 또다른 weight를 만들어 더 효율적으로 계산하는 방식은 다음과 같이 나타낼 수 있다: (파라미터 \(\Theta\)에 대해 \(\Delta\Phi=\Delta\Phi(\Theta), |\Theta|<<|\Phi_0|\))

\[\underset{\Phi}{max}\sum_{(x,y)\in Z}\sum^{|y|}_{t=1}\log{(P_{\Phi_0+\Delta\Phi(\Theta)}(y_t|x,y<t))}\]

즉 기존의 잘 학습된 weight는 그대로 두고 low rank로 decomposition 된 weight만 optimization 하는 방법론을 Low Rank Adaptation(LoRA)라고 한다.

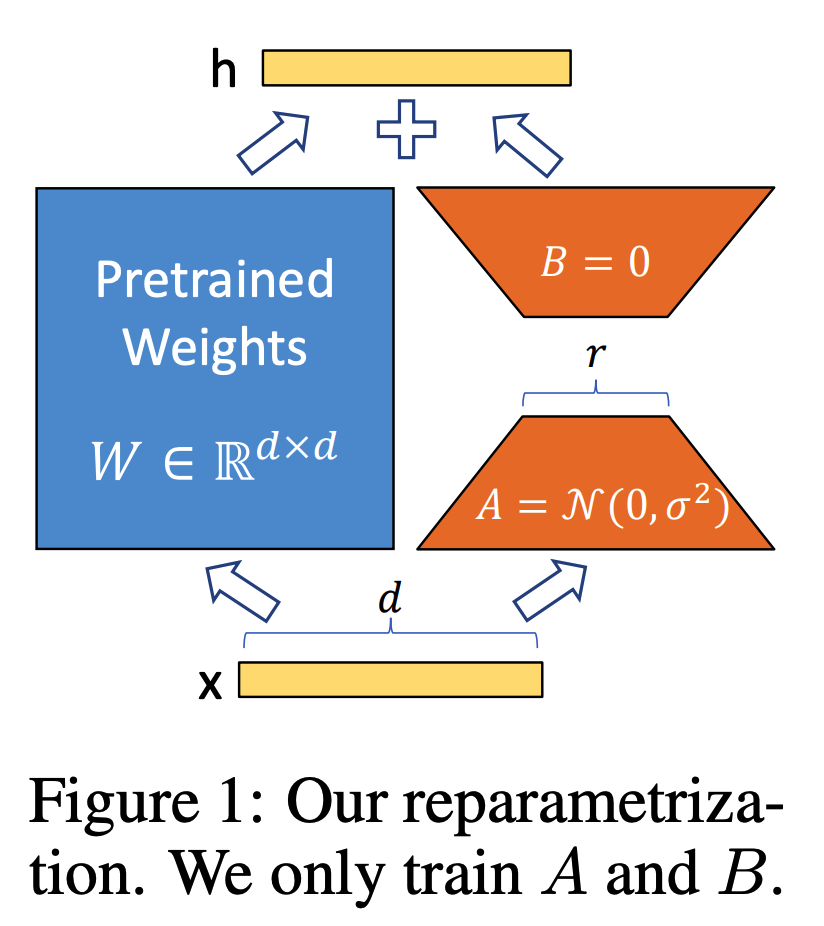
Low Rank Adaptation

Fig. 562 Low Rank Adaptation#

위의 그림과 같이 원본 모델 weight는 freeze, LoRA는 rank를 r로 낮추어 finetuning한다. 이때 LoRA의 A는 random Gauissian으로, B는 zero로 weight initializing 한다.

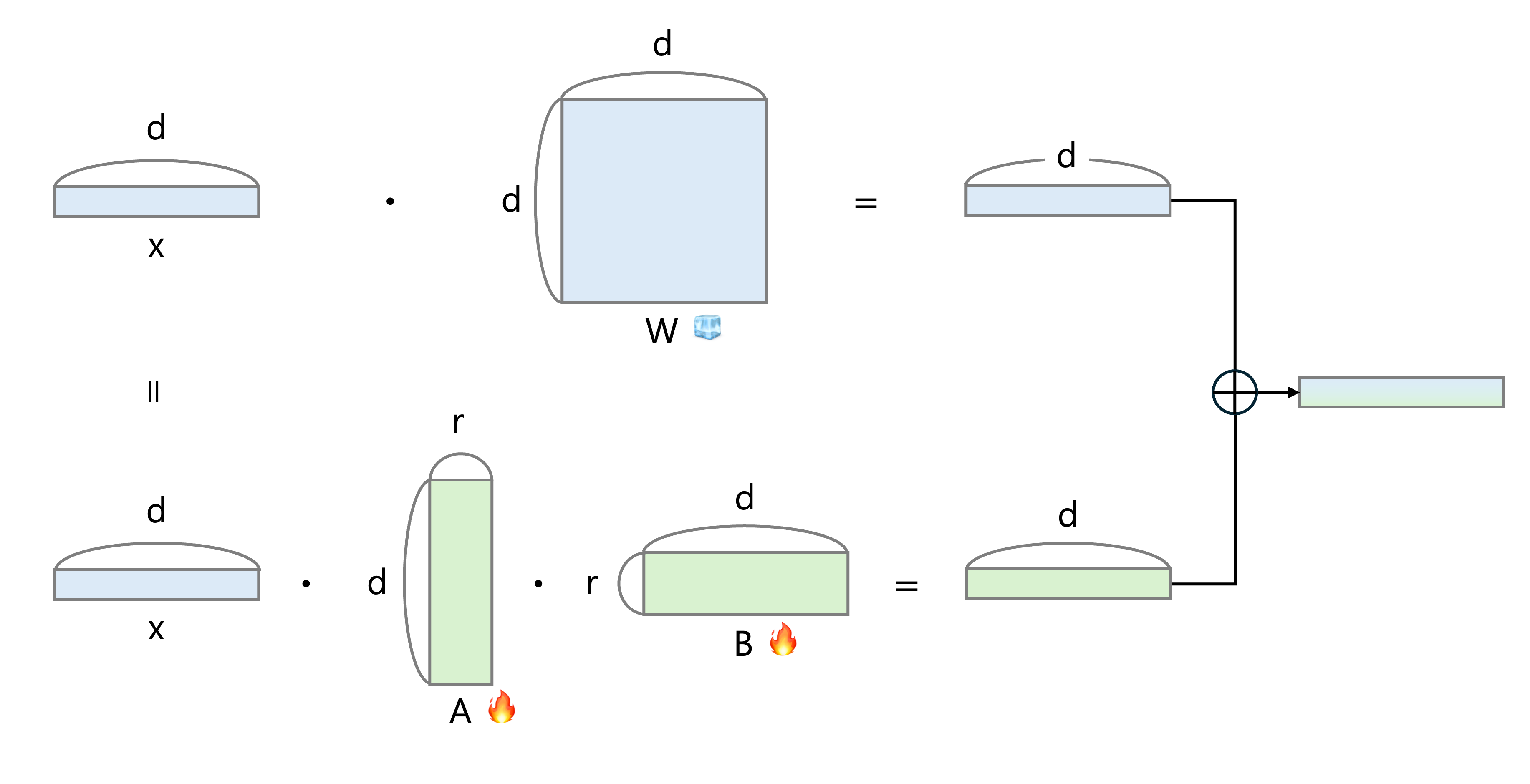
Low Rank Adaptation matrix

Fig. 563 Low Rank Adaptation matrix#

위 그림처럼 기존에는 d x d의 매우 큰 weight를 finetuning 해야 했지만, LoRA는 r만큼 압축된 weight matrix만 finetuning 하면 되기 때문에 훨씬 효율적이고 때에 따라 Fully fine-tuning 하는 방법들보다 더 좋은 성능을 보여주기도 한다. (그림은 이곳을 참고하였습니다.)

원본 논문의 LoRA는 LLM을 target으로 만들어졌기 때문에 Transformer의 query, key, value에 대한 parameter로 사용하였지만 Diffusion이나 다른 모델의 finetuning시에도 간단하게 사용 가능하다.

Task Arithmetic in Pretrained Models#

task Arithmetic은 특정 task에서 학습된 Model의 가중치를 task vector라 보고 각 task vector를 조합하여 새로운 task vector를 생성하는 방법론이다.

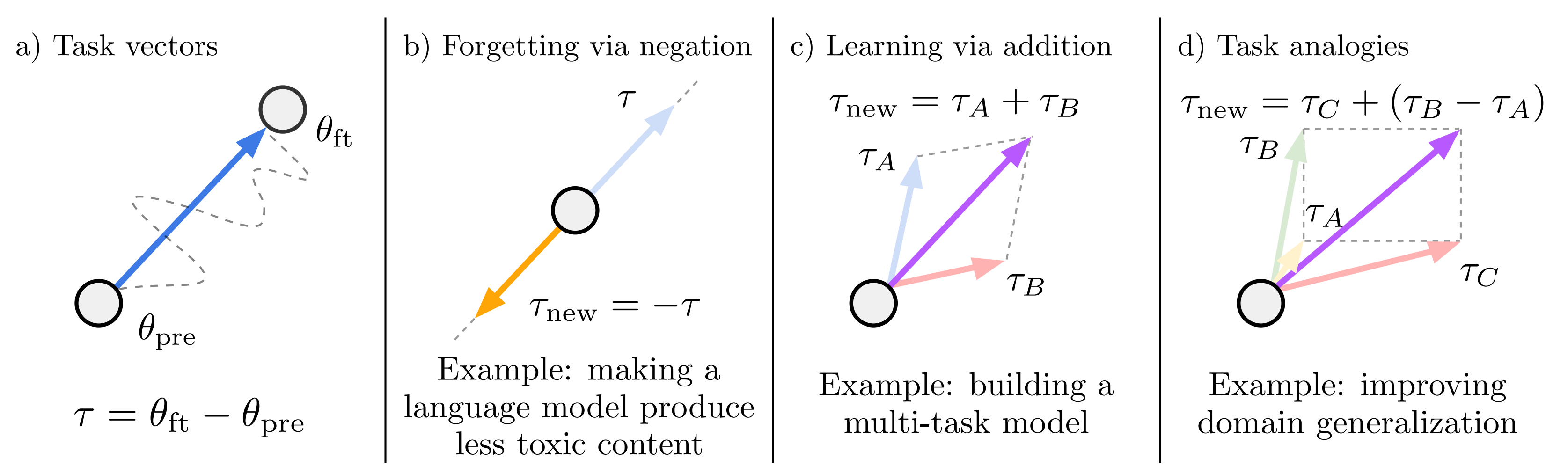
Task Arithmetic

Fig. 564 Task Arithmetic#

pre-trained parameter를 \(\theta_{pre}\), fine-tuning parameter를 \(\theta_{ft}\)라고 할때 task vector \(\tau\)는 \(\theta_{ft}-\theta_{pre}\)로 정의할 수 있다. 이를 다양하게 조합하고 특히 d)처럼 task 간 analogy를 고려하여 연산하는 경우 새로운 task에 대한 성능을 높일 수 있다.

3. LCM-LoRA#

3.1 LoRA Distillation for LCM#

LCMs의 Latent Consistency Distillation에 대한 pseudo code는 다음과 같다:

Latent Consistency Distillation

Fig. 565 Latent Consistency Distillation#

논문의 저자는 LCMs의 Distillation은 LDMs에 관한 일종의 fine-tuning으로 보고 LoRA를 적용하는 방법을 제안하였다. pre-trained 된 weight matrix \(W_0\)에 대하여 기울기 업데이트는 \(W_0+\Delta W=W_0+BA, W_0\in \mathbb{R}^{d\times k}, B\in \mathbb{R}^{d\times r}, A\in \mathbb{R}^{r\times k}\) 로 표현할 수 있으며 rank \(r \leq \min{(d,k)}\) 로 작은 값을 갖는다. \(W_0\)의 weight는 고정되며 input \(x\) 에 대한 forward pass는 다음과 같다:

\[h=W_0x+\Delta Wx=W_0x+BAx. \tag{1}\]

위와같이 LCMs에 LoRA를 적용할 경우 학습 parameter를 크게 줄일 수 있어 효율적이다.

compare trainable parameter

Fig. 566 compare trainable parameter#

따라서 LCM-loRA는 기존 LCMs 보다 더 큰 모델의 훈련과 실사용이 가능하다. LCMs의 경우 SD-V1.5나 SD-V2.1의 base Stable Diffusion을 사용했지만, LCM-LoRA는 SDXL과 SSD-1B(Segmind)을 확장하여 사용하였다. large Model에서도 LCD을 적용했을 때 잘 적응하는 모습을 볼 수 있었다.

1024 x 1024 resolution image results with CFG scale w=7.5

Fig. 567 1024 x 1024 resolution image results with CFG scale w=7.5#

3.2 LCM-LoRA as Universal Acceleration Module#

LCM-LoRA는 sampling step을 줄이는 distillation에 LoRA를 적용하였다. LoRA는 이외에도 custionized datasets에 대해 fine-tuning할 때 주로 쓰이는데 이같은 style에 대한 LoRA와 LCM-LoRA가 추가 학습없이 바로 합쳐져 사용할 수 있음을 발견했다. 저자는 이 발견이 task arithmetic에 대한 관점으로 해석할 수 있다고 주장하였다.

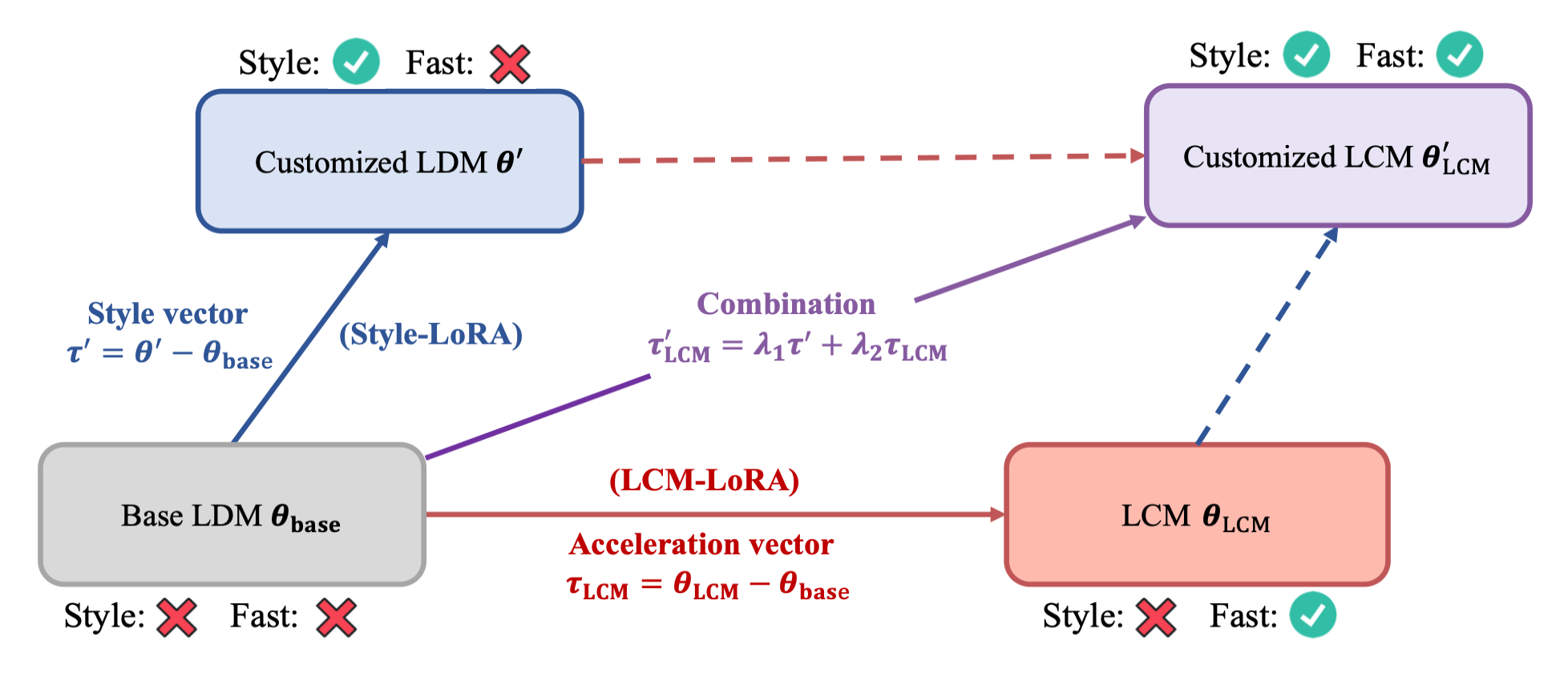
Style-LoRA with LCM-LoRA

Fig. 568 Style LoRA with LCM-LoRA#

LCM-LoRA의 fine-tuned parameter를 \(\tau_{LCM}\)이라 할 때, \(\tau_{LCM}\)은 acceleration vector라 할수 있다. 그리고 custom dataset에서 학습한 LoRA의 fine-tuned parameter를 \(\tau'\)이라 할 때, \(\tau'\)은 style vector라 할 수 있다. LCMs를 통해 custom dataset에 대한 image를 생성할 때, 파라미터는 다음과 같이 조합된다:

\[\theta'_{LCM}=\theta_{pre}+\tau'_{LCM} \tag{2}\]
\[\tau'_{LCM}=\lambda_1\tau'+\lambda_2\tau_{LCM} \tag{3}\]

파라미터는 단순한 선형 결합을 통해 이루어지며 \(\lambda_1\)과 \(\lambda_2\)는 하이퍼파라미터다. 추가적인 학습없이 다음과 같은 결과를 얻을 수 있었다:

fine-tuning with LCM-LoRA

Fig. 569 fine-tuning with LCM-LoRA#

4. Conclusion#

  • training-free acceleration module인 LCM-LoRA를 제안.

  • PF-ODE를 예측하며 Stable Diffusion 및 SD LoRA에 fast inference, minimal step을 제공함.

  • 강력한 일반화 성능 증명.

Contents