Information
Title: Denoising Diffusion Implicit Models (ICLR 2021)
Reference
Code: Official:
Author: Seunghwan Ji
Last updated on April. 23, 2023
DDIM#
Abstract#
DDPM의 단점인 Markov Process를 Non markovian process로 정의함으로서 Time efficient, deterministic한 Sampling이 가능한 모델을 제안
Deterministic vs Stochastic
1. Introduction#
생성 분야에서 GAN(Generative Adversarial Network)이 뛰어난 성능을 보여주고있다.
하지만, GAN은 학습 과정에서 불안정성을 보이는 경우가 많다.
Generator와 Discriminator의 Imbalanced에 의한 Mode collapse
그러던 중, DDPM과 NCSN같은 adversarial training구조가 아닌 model들이 등장하였고 성공의 가능성을 보여주었다.
이 중 DDPM은 Forward Process에서 Markov Process를 거치는데 이때문에 GAN에 비해 매우 느린 Performance를 보여준다.
sampling
GAN
DDPM
32 x 32 x 50k
Less than 1 min
About 20h
256 x 256 x 50k
-
About 1000h
DDIM은,
Markov Chain에 기반한 Process를 Non Markovian Process로 대체하였고
결국 좀더 빠르고 비교적 우수한 Quality의 결과를 생성해내고, (with accelate)
DDPM과는 다르게 Consistency한 학습 결과를 보여줌으로써 latent간의 Interpolation이 가능하다.
Consistency?
If x, y is equivalent, then f(x) = f(y)
2. Background#
DDPM#
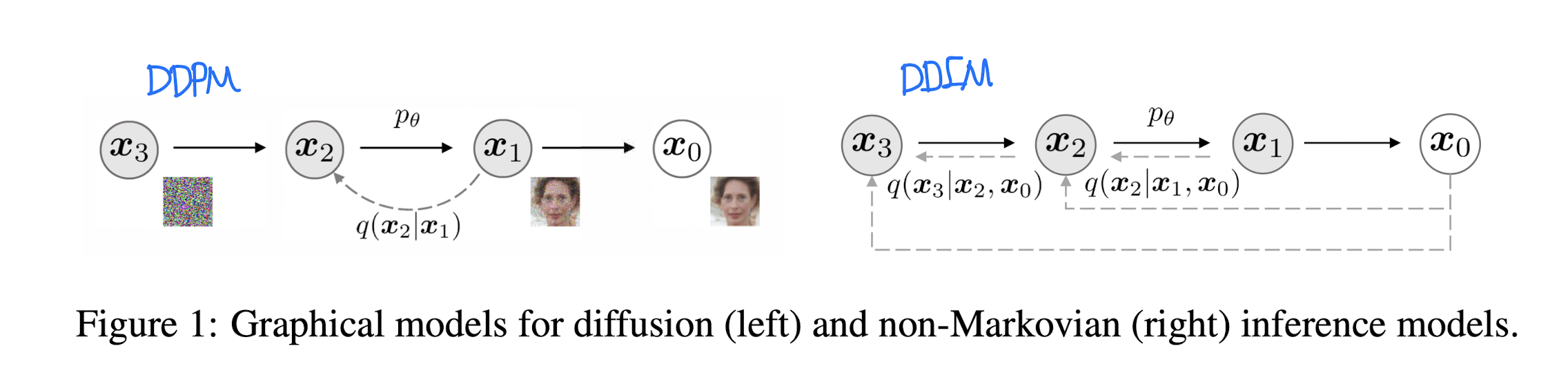
Fig. 23 DDPM & DDIM Architectures#
DDPM의 Forward Process는 Markov process로 동작한다.
Markov process
미래 시점을 예측하기위해 현재 시점의 값을 이용한다.
미래 시점은 과거 시점의 값에는 독립적인 값을 갖는다.
time step T는 DDPM에서 성능을 좌지우지하는 중요한 Hyper parameter이다. (대충 T=1000 정도?)
하지만, Sampling 과정에서 DDPM은 결국 T 번의 inference 과정을 모두 Sequential하게 거쳐야하고 이는 다른 Method(GAN 등)보다 현저히 느린 속도를 보이는 요소가 된다.
3. Variational Inference For Non-Markovian Forward Process#
3.1. Non-Markovian Forward Processes
Inference’s Distribution 정의
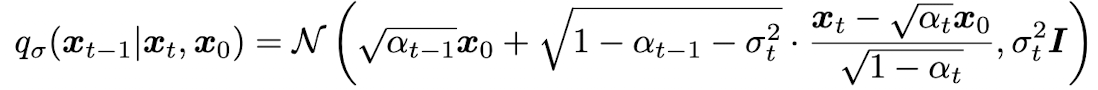
Fig. 24 Equation 1#
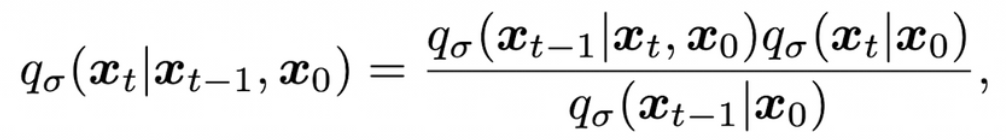
Fig. 25 Equation 2#
t 시점의 값을 구하기위해 \(X_{t-1}\)의 값과 \(X_{0}\)의 값을 참조
DDPM은? \(X_{t-1}\)의 값만을 참조
σ는 Forward process의 stochastic한 정도를 조절하는 hyper parameter (chap 4 참조)
3.2. Generative Process And Unified Variational Inference Objective (Reverse Process)
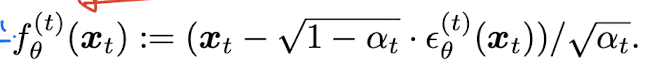
Fig. 26 Equation 3#
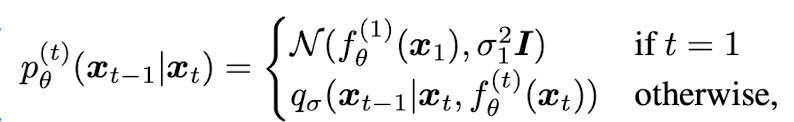
Fig. 27 Equation 4#
\(X_{t}\)을 통해 \(X_{0}\)의 값을 예측 (trainable)
위의 식을 통해 \(X_{t}\)와, \(X_{0}\)의 값을 이용해 \(X_{t-1}\)을 샘플링
실제로는
noise(ε)와 \(X_{0}\), \(X_{t}\)의 관계
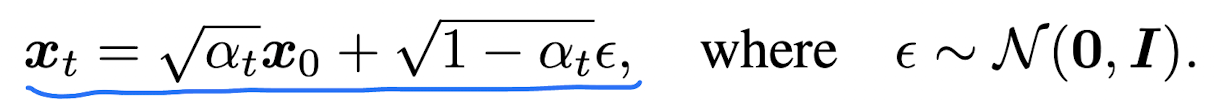
Fig. 28 Equation 5#
\(X_{t}\)을 통해 \(X_{0}\)을 예측
t 시점의 이미지를 통해 t 시점의 noise를 예측
t 시점의 이미지와 t 시점의 noise를 통해 0 시점의 이미지를 계산 (fixed)
위의 식을 통해 t시점의 값과 예측한 0 시점의 값을 이용해 t-1 시점의 값을 샘플링
4. Sampling From Generalized Generative Process#
4.1. Denoising Diffusion Implicit Models
If σ → 0

Fig. 29 Equation 6#
σ가 특정 값을 가질 때 DDPM의 generative process의 수식과 동일하다.
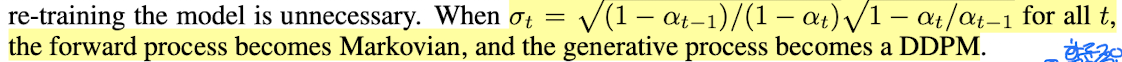
Fig. 30 Explanation of σ#
4.2. Accelerated Generation Processes
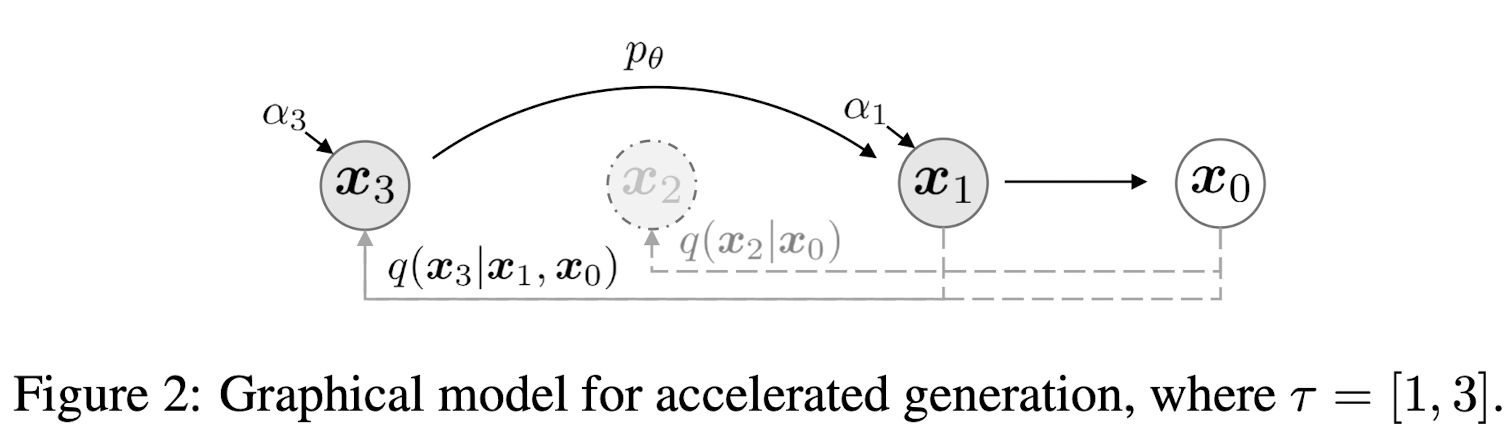
Fig. 31 Explanation of accelated method#
DDIM은 Deterministic하기때문에 모든 시점의 값을 모두 계산할 필요 없이 subset의 시점만으로 sampling이 가능하다.
이 Accelerating method는 약간의 quality 저하가 있지만 Computational efficiency를 충분히 증가시킬 수 있다.
DDIM 방식의 재학습 없이 DDPM의 training에 DDIM의 sampling이 가능하다.
4.3. Relevance To Neural ODEs
DDIM은 Object(e.g. 이미지)의 Encoding이 가능한 식을 유도할 수 있다.
5. Experiments#
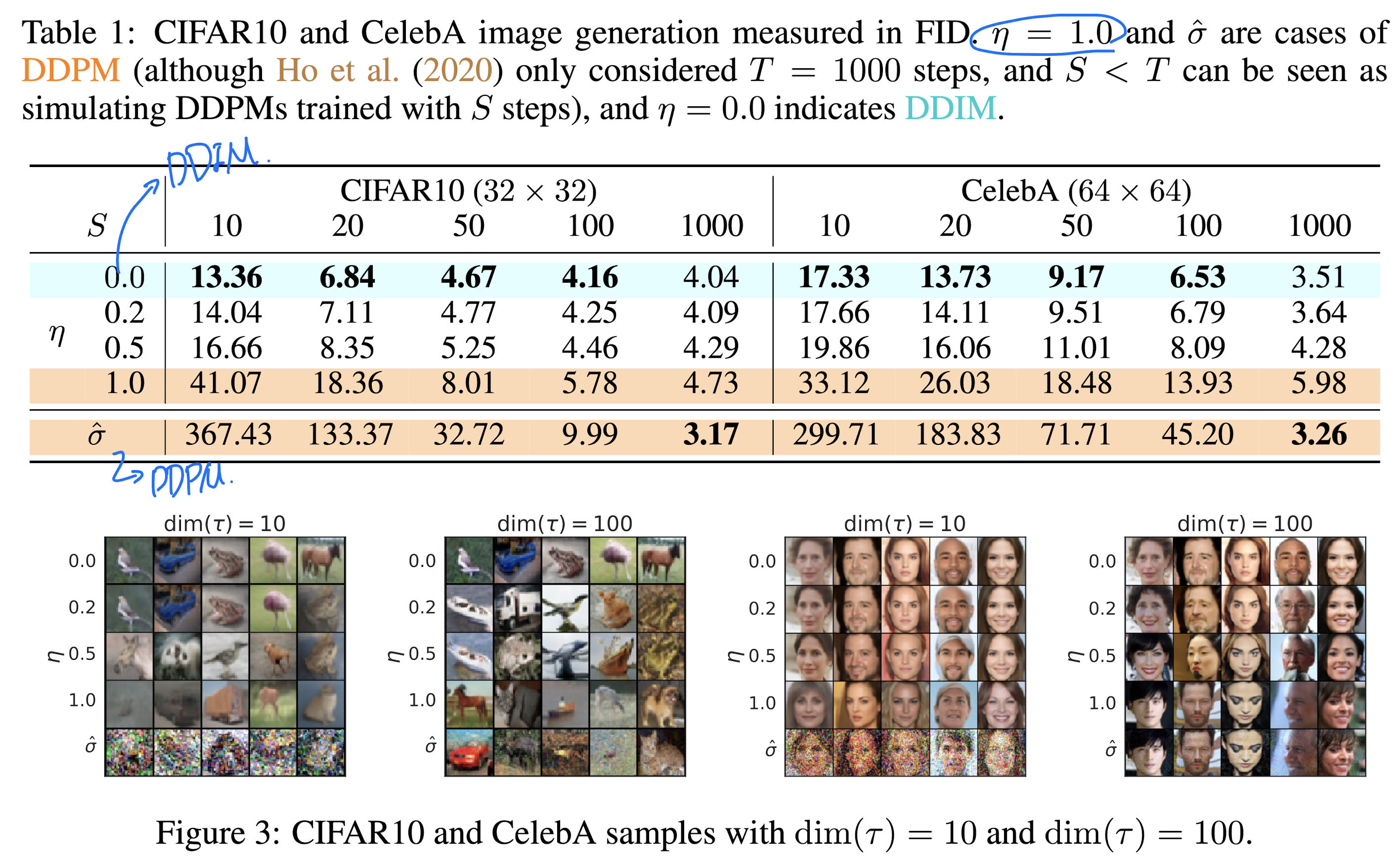
Fig. 32 Table1#
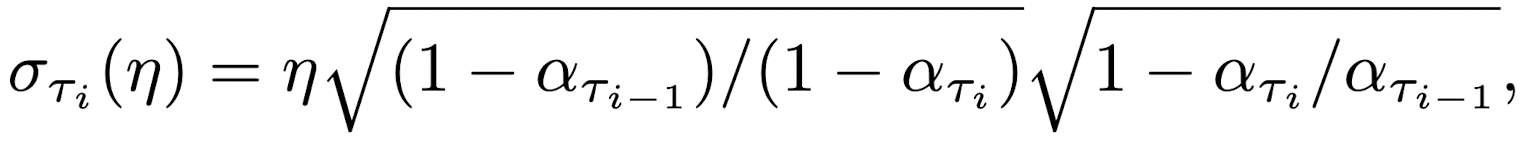
Fig. 33 Euqation 7#
η → model을 simple하게 control하기위한 hyperparameter
η = 1 → Model is DDPM
η = 0 → Model is DDIM
모든 비교 모델이 S(sampling 횟수)의 값이 커질수록 더 낮은 FiD를 보여준다.
Fig.3의 DDIM은 다른 모델(η가 0이 아닌 모델)과 다르게 sampling step에 consistency한 결과를 보여준다.
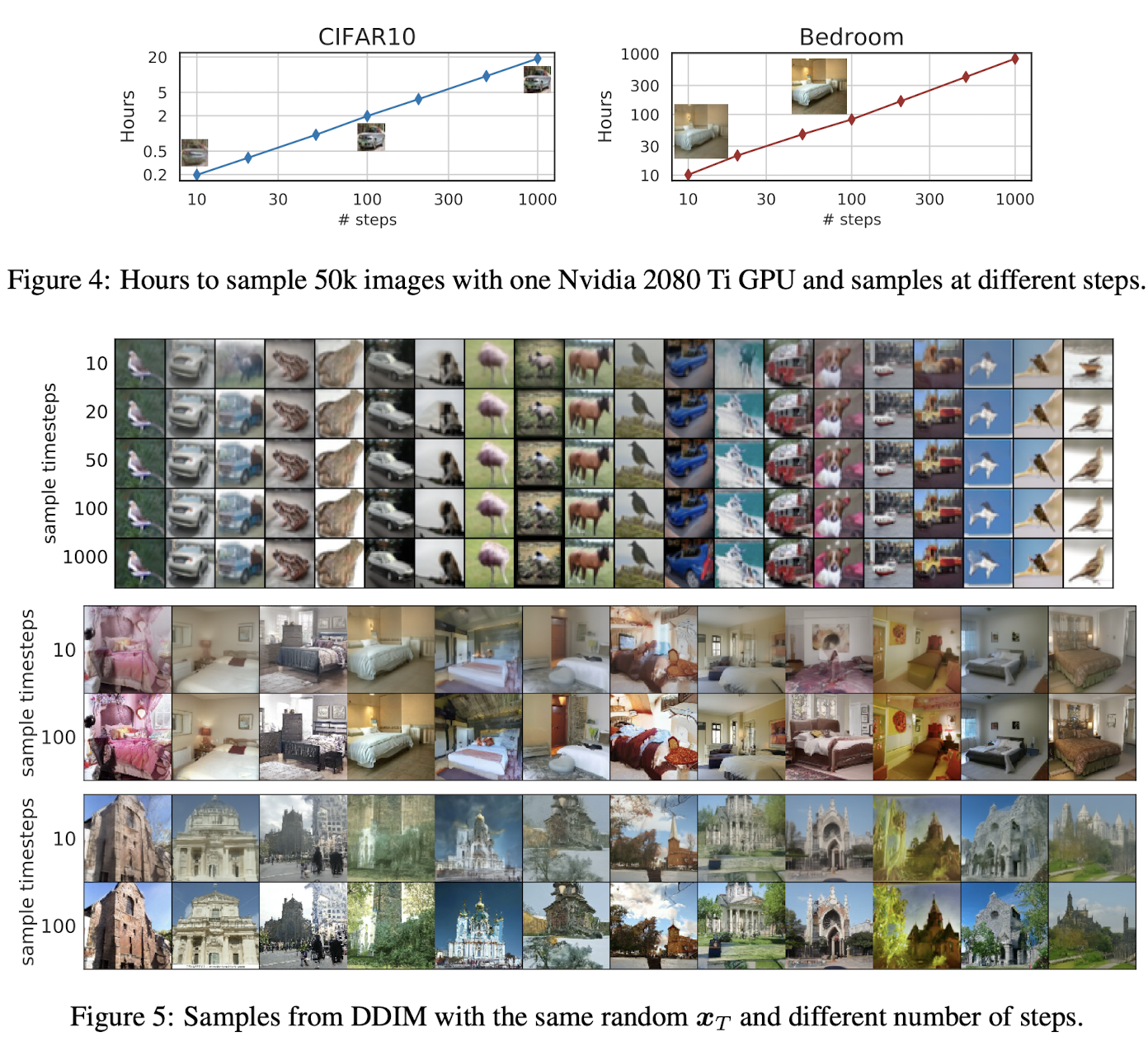
Fig. 34 Figure 4, 5#
Step과 Inference time이 linear한 관계를 갖는다.
적은 sampling step에서도 어느정도의 object를 보여준다.

Fig. 35 Figure 6#
T 시점의 이미지에 interpolation이 가능하다.
6. Code#
# https://keras.io/examples/generative/ddim/
class DiffusionModel(keras.Model):
def __init__(self, image_size, widths, block_depth):
super().__init__()
self.normalizer = layers.Normalization()
self.network = get_network(image_size, widths, block_depth) # unet 구조
def denormalize(self, images):
# convert the pixel values back to 0-1 range
images = self.normalizer.mean + images * self.normalizer.variance**0.5
return tf.clip_by_value(images, 0.0, 1.0)
def diffusion_schedule(self, diffusion_times):
# diffusion times -> angles
start_angle = tf.acos(max_signal_rate)
end_angle = tf.acos(min_signal_rate)
diffusion_angles = start_angle + diffusion_times * (end_angle - start_angle)
# angles -> signal and noise rates
signal_rates = tf.cos(diffusion_angles)
noise_rates = tf.sin(diffusion_angles)
# note that their squared sum is always: sin^2(x) + cos^2(x) = 1
return noise_rates, signal_rates
def denoise(self, noisy_images, noise_rates, signal_rates, training):
# the exponential moving average weights are used at evaluation
if training:
network = self.network
else:
network = self.ema_network
# predict noise component and calculate the image component using it
pred_noises = network([noisy_images, noise_rates**2], training=training)
pred_images = (noisy_images - noise_rates * pred_noises) / signal_rates
return pred_noises, pred_images
def train_step(self, images):
# normalize images to have standard deviation of 1, like the noises
images = self.normalizer(images, training=True)
noises = tf.random.normal(shape=(batch_size, image_size, image_size, 3))
# sample uniform random diffusion times
diffusion_times = tf.random.uniform(
shape=(batch_size, 1, 1, 1), minval=0.0, maxval=1.0
)
noise_rates, signal_rates = self.diffusion_schedule(diffusion_times)
# mix the images with noises accordingly
noisy_images = signal_rates * images + noise_rates * noises
with tf.GradientTape() as tape:
# train the network to separate noisy images to their components
pred_noises, pred_images = self.denoise(
noisy_images, noise_rates, signal_rates, training=True
)
noise_loss = self.loss(noises, pred_noises) # used for training
image_loss = self.loss(images, pred_images) # only used as metric
gradients = tape.gradient(noise_loss, self.network.trainable_weights)
self.optimizer.apply_gradients(zip(gradients, self.network.trainable_weights))
self.noise_loss_tracker.update_state(noise_loss)
self.image_loss_tracker.update_state(image_loss)
return {m.name: m.result() for m in self.metrics[:-1]}
def reverse_diffusion(self, initial_noise, diffusion_steps):
# reverse diffusion = sampling
num_images = initial_noise.shape[0]
step_size = 1.0 / diffusion_steps
# important line:
# at the first sampling step, the "noisy image" is pure noise
# but its signal rate is assumed to be nonzero (min_signal_rate)
next_noisy_images = initial_noise
for step in range(diffusion_steps):
noisy_images = next_noisy_images
# separate the current noisy image to its components
diffusion_times = tf.ones((num_images, 1, 1, 1)) - step * step_size
noise_rates, signal_rates = self.diffusion_schedule(diffusion_times)
pred_noises, pred_images = self.denoise(
noisy_images, noise_rates, signal_rates, training=False
)
# network used in eval mode
# remix the predicted components using the next signal and noise rates
next_diffusion_times = diffusion_times - step_size
next_noise_rates, next_signal_rates = self.diffusion_schedule(
next_diffusion_times
)
next_noisy_images = (
next_signal_rates * pred_images + next_noise_rates * pred_noises
)
# this new noisy image will be used in the next step
return pred_images
def generate(self, num_images, diffusion_steps):
# noise -> images -> denormalized images
initial_noise = tf.random.normal(shape=(num_images, image_size, image_size, 3))
generated_images = self.reverse_diffusion(initial_noise, diffusion_steps)
generated_images = self.denormalize(generated_images)
return generated_images
