Information

• Title: Consistency Models (ICML 2023)

• Reference

  • Paper: https://arxiv.org/pdf/2303.01469

  • Code: openai/consistency_models

• Author: Sangwoo Jo

• Last updated on Apr. 26, 2024

Consistency Models

1. Introduction

Diffusion Models 은 image generation, audio synthesis, video generation 등의 다양한 분야에 연구가 진행되어 왔습니다. 하지만 single-step generative model 인 VAE, GAN, 그리고 normalizing flows 에 비해 추론 속도가 10-2000배 더 많은 연산작업을 요하는 치명적인 단점이 존재합니다.

이러한 문제를 해결하기 위해 논문에서 Consistency Model 을 소개합니다.

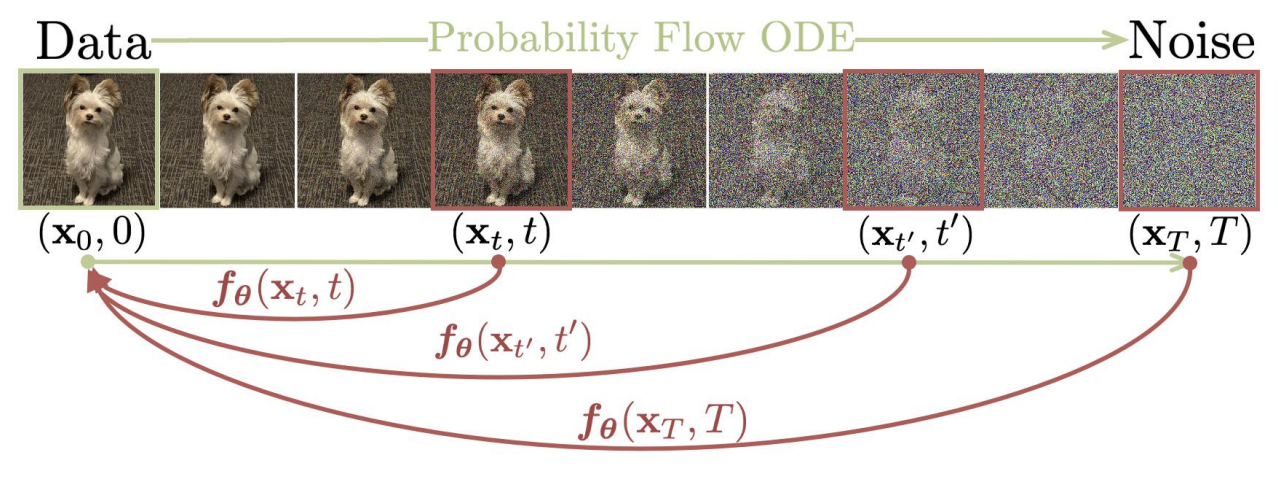
Fig. 480 Overview of Consistency Models

위의 사진처럼 주어진 PF ODE (Probability Flow Ordinary Differential Equation) 에 대해서 동일한 trajectory 에 있는 point 들이 동일한 시작점으로 매핑되도록 모델을 학습하는 방식을 제안하고, 이러한 self-consistency 특성을 만족시킬 수 있도록 2가지 학습 방식을 소개합니다.

1. 첫번째 방식으로는 우선적으로 numerical ODE solver 와 사전 학습된 diffusion model을 사용하여 PF ODE trajectory 에서 인접한 point 쌍을 생성합니다. 그리고 이러한 쌍에 대한 모델 출력 간의 차이를 최소화하도록 모델을 학습함으로써 diffusion model 을 consistency model 로 효과적으로 knowledge distillation 을 적용할 수 있고, 단 한번의 step 만으로도 high quality sample 을 생성할 수 있게 됩니다.

2. 두번째 방식으로는 사전학습된 diffusion model 에 의존하지 않고 독립적으로 consistency model 을 학습하는 방식입니다.

CIFAR-10, ImageNet 64x64, LSUN 256x256 데이터셋에 실험한 결과, 기존 distillation 기법을 적용한 모델 (i.e., progressive distillation) 보다 성능이 개선되고, 독립적인 모델로서도 사전학습된 diffusion model 없이 GAN 을 제외한 single-step generative model 보다 성능이 좋다고 합니다. 마지막으로 다양한 zero-shot data editing (image denoising, interpolation, inpainting, colorization, super-resolution, stroke-guided image editing) task 에도 consistency model 이 좋은 성능을 보여준다는 것을 확인하였습니다.

2. Diffusion Models

Diffusion Models in Continuous Time

Continuous time 에서의 diffusion model 을 다음과 같이 SDE 수식으로 표현할 수 있습니다. (Song et al., 2021)

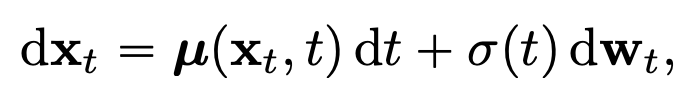
Fig. 481 Diffusion Models in Continuous Time

• \(t \in [0,T], T > 0\)

• \(\mu(\cdot,\cdot), \sigma(\cdot)\) := drift, diffusion coefficients

• \(\{w_t\}_{t \in [0,T]}\) := standard Brownian motion

그리고 해당 SDE 는 아래 식과 같은 PF ODE 로 표현할 수 있다는 성질을 가지고 있습니다. 이때 \(\nabla \log p_t(x_t)\) 를 score function 이라고 하고, 시점 t 에 대한 solution trajectory 가 \(p_t(x)\) 에 따라 분포합니다.

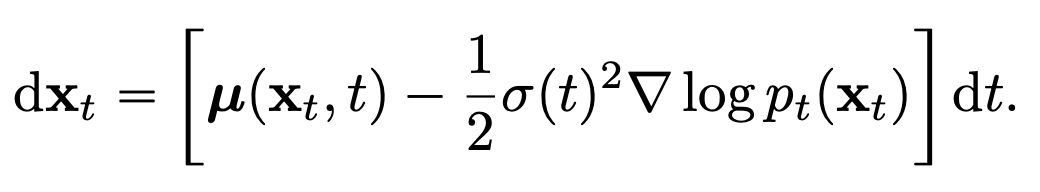
Fig. 482 Probability Flow (PF) ODE

일반적으로 위의 SDE 수식에서 \(p_T(x)\) 가 Gaussian distribution \(\pi(x)\) 를 따르도록 정의하고, 해당 논문에서 Karras et al., 2022 와 동일하게 \(\mu(x,t) = 0, \sigma(t) = \sqrt{2}t\) 로 설정하였습니다. 그리고 sampling 시, score matching 을 통해 score model \(s_{\phi}(x,t) \approx \nabla \log p_t(x)\) 우선적으로 학습한 후, 위의 식에 대입하면 다음과 같은 empirical PF ODE 로 표현할 수 있습니다

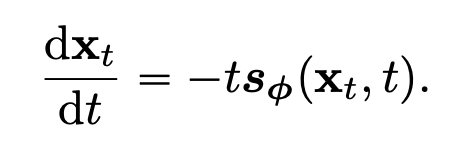
Fig. 483 Empirical PF ODE

다음 과정으로는 initial condition \(x_T \sim N(0, T^2I)\) 을 기반으로 Euler 나 Heun 등의 numerical ode solver 를 통해 역방향으로 풀어 solution trajectory \(\{x_t\}_{t \in [0,T]}\)\({x_t}\)\(\hat{x}_0\)\({x_t}\)\(p_{data}(x)\) 로부터 나온 샘플에 대한 근사값이라고 할 수 있습니다.

추가적으로 논문에서 numerical instability 를 방지하기 위해 고정된 작은 양수 \(\epsilon\) 에 대해 \(t = \epsilon\) 에서 solver 를 멈추고 \(\hat{x}_{\epsilon}\) 를 \(p_{data}(x)\) 에 대한 근사값으로 간주합니다. 그리고 Karras et al., 2022 와 동일하게 이미지 픽셀 값을 \([-1,1]\) 로 rescale 하고 \(T = 80, \epsilon = 0.002\) 로 설정합니다.

앞서 소개드린 방식으로 diffusion model 을 통한 sampling 시, ode solver 를 사용하는데 score model \(s_{\phi}(x_t,t)\) 의 수많은 iterative evaluation 작업이 필요합니다. 빠른 sampling 작업을 위해, 더 빠른 numerical ode solver 에 대한 연구들이 진행되었지만, 이를 활용해도 최소 10번 이상의 evaluation step 을 거쳐야만 competitive 한 성능을 보여준다고 합니다. 여러 distillation 기법들에 대한 연구들도 진행되었지만, Salimans & Ho (2022) 를 제외하고는 distillation 작업을 하기 위해서 사전에 diffusion model 로부터 대량의 데이터를 수집해야한다는 단점이 있습니다.

3. Consistency Models

논문에서 single-step generation 이 가능한 consistency model 을 제안하고, 학습하는 방식으로 1) 사전학습된 diffusion model 로부터 knowledge distillation 진행하는 방식과 2) 독립적으로 학습하는 방식 을 소개합니다.

Definition

주어진 PF ODE 에 대한 trajectory \(\{x_t\}_{t \in [0,T]}\) 에 대해서 다음과 같은 consistency function \(f : (x_t, t) \mapsto x_{\epsilon}\) 을 정의하고, 함수 \(f\) 는 동일한 trajectory 에 있는 임의의 두 \(t, t' \in [\epsilon, T]\) 에 대해 \(f(x_t, t) = f(x_{t'}, t')\), 즉 self-consistency 성질을 만족합니다. 이러한 함수 \(f\) 를 예측하기 위해 데이터로부터 \(f_{\theta}\) 을 학습하는 것이 consistency model 의 objective 이며, 이는 Bilos et al., 2021 에서 정의하는 neural flow 와 유사하지만, consistency model 은 invertible property 를 부여하지는 않습니다.

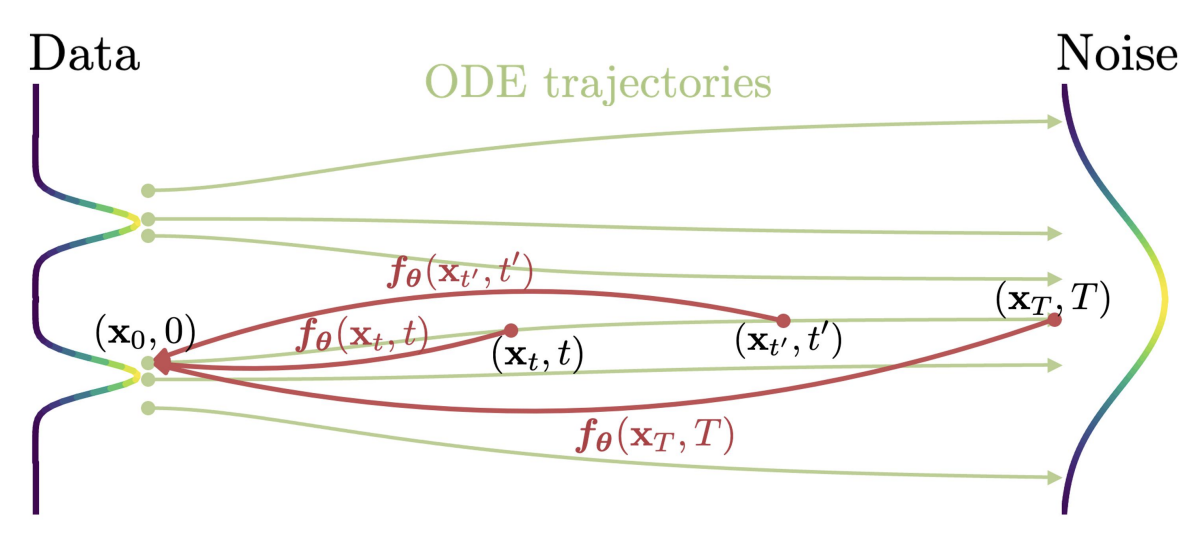
Fig. 484 Self-Consistency

Parameterization

앞서 정의한 부분에 의해, 모든 consistency function \(f\) 에 대해서 \(f(x_{\epsilon}, t) = x_{\epsilon}\) 를 만족해야 하는 boundary condition 이 존재하고, 이를 만족하기 위해 다음과 같이 두 가지 방식으로 parameterization 방식을 정의하였습니다.

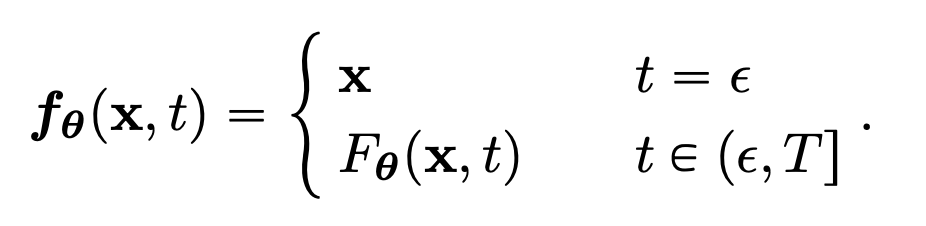
Fig. 485 Parameterization Method 1

여기서 \(F_{\theta}(x,t)\) 는 output 차원이 \(x\) 와 동일한 free-form deep neural network 입니다. 두번째 방식으로는, 다음과 같이 skip-connection 을 활용합니다.

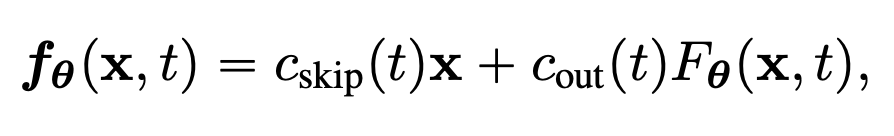
Fig. 486 Parameterization Method 2

이때, \(F_{\theta}(x,t), c_{skip}(t), c_{out}(t)\) 는 \(c_{skip}(\epsilon) = 1, c_{out}(\epsilon) = 0\) 조건을 만족시키는 미분 가능한 함수로 정의합니다.

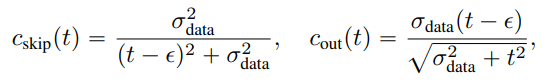
Fig. 487 Parameterization Method 2 - \(c_{skip}(t), c_{out}(t)\)

두번째 parameterization 기법이 diffusion model 형식과 매우 유사하여 이러한 diffusion model 아키텍쳐를 leverage 하기 위해 논문에서 두번째 방식으로 parameterization 을 하는 방식을 택합니다.

Sampling

학습된 consistency model \(f_{\theta}(\cdot,\cdot)\) 와 initial distribution \(\hat{x}_T \sim N(0, T^2I)\) 를 활용하여 단일 sampling step 만으로 \(\hat{x}_{\epsilon} = f_{\theta}(\hat{x}_{T}, T)\) 를 생성할 수 있습니다. 더불어 하단 pseudo code 에 보이듯이, denoising 과 noise injection 작업을 여러 번 거치는 multistep consistency sampling 을 통해 computing cost 와 sample quality 를 trade-off 할 수 있는 유연성도 제공합니다.

Fig. 488 Multistep Consistency Sampling

Zero-Shot Data Editing

Diffusion model 과 유사하게 추가적인 학습 없이 zero-shot 형태로 image editing 그리고 manipulation task 이 가능합니다. 예를 들어, consistency model 은 Gaussian noise 로부터 one-to-one mapping 을 통해 \(x_{\epsilon}\)을 생성하기 때문에 GAN, VAE, normalizing flow 와 유사하게 latent space 을 통해 sample 들간의 interpolation 이 가능합니다. 또한, multistep consistency sampling 을 통해 zero-shot 의 한계점을 보완하면서 image editing, inpainting, colorization, super-resolution, stroke-guided image editing (Meng et al., 2021) 등의 다양한 task 를 수행할 수 있습니다. 대표적으로 몇 가지 zero-shot image editing 결과 예시들을 공유합니다.

• Inpainting

  

  Fig. 489 Consistency Models - Inpainting

• Interpolation

  

  Fig. 490 Consistency Models - Interpolation

• Self-consistency

  

  Fig. 491 Consistency Models - Self-consistency

4. Training Consistency Models via Distillation

앞서 소개한 두 가지 학습 방식 중, 첫번째로 사전학습된 score model \(s_{\phi}(x,t)\) 를 consistency model 에 knowledge distillation 하는 학습하는 방식을 소개합니다.

논문에서 특히 continuous time interval \([\epsilon, T]\) 을 boundary \(t_1 = \epsilon < t_2 < \cdots < t_N=T\) 를 기준으로 \(N-1\) 개의 interval 로 discretize 하는 상황을 가정하고, Karras et al., 2022 의 설정과 동일하게 boundary 를 다음과 같이 정의합니다.

\[ t_i = (\epsilon^{1/\rho} + \frac{i-1}{N-1}(T^{1/\rho}-\epsilon^{1/\rho}))^{\rho}, \quad \rho = 7 \]

이때, \(N\) 이 충분히 크다면 다음과 같이 numerical ode solver 의 discretization step 을 한번 진행시켜 \(x_{t_{n+1}}\) 로부터 \(x_{t_n}\) 에 대한 정확한 예측값을 얻을 수 있다고 합니다.

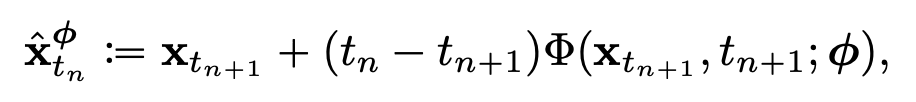
Fig. 492 One Discretization Step of a Numerical ODE Solver

이때, \(\Phi(\cdots; \phi)\) 은 empirical PF ODE 에 적용되는 one step ODE solver 의 update function 입니다. Euler solver 같은 경우, \(\Phi(x,t;\phi) = -ts_{\phi}(x,t)\) 를 대입하면 다음과 같이 표현할 수 있게 됩니다.

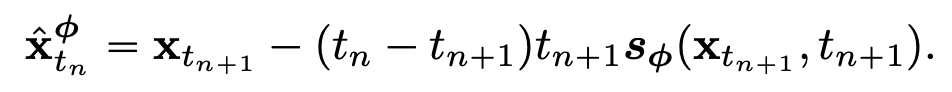
Fig. 493 One Discretization Step of a Euler ODE Solver

위 수식을 활용하여 주어진 \(x \sim p_{data}\) 에 대해서 PF ODE trajectory 에 있는 인접한 두 지점 \((\hat{x}^{\phi}_{t_n}, x_{t_{n+1}})\) 을 샘플링할 수 있게 됩니다. 더 자세하게는, \(x_{t_{n+1}} \sim N(x,t^2_{n+1}I)\) 를 우선적으로 샘플링한 후, 위 수식을 기반으로 numerical ode solver 의 discretization step 을 한번 거쳐 \(\hat{x}^{\phi}_{t_n}\) 을 계산합니다. 최종적으로 \((\hat{x}^{\phi}_{t_n}, x_{t_{n+1}})\) 로부터의 모델 출력값 차이를 최소화하도록 consistency model 을 학습하게 되고, 학습 시 사용되는 consistency distillation loss 는 다음과 같이 정의합니다.

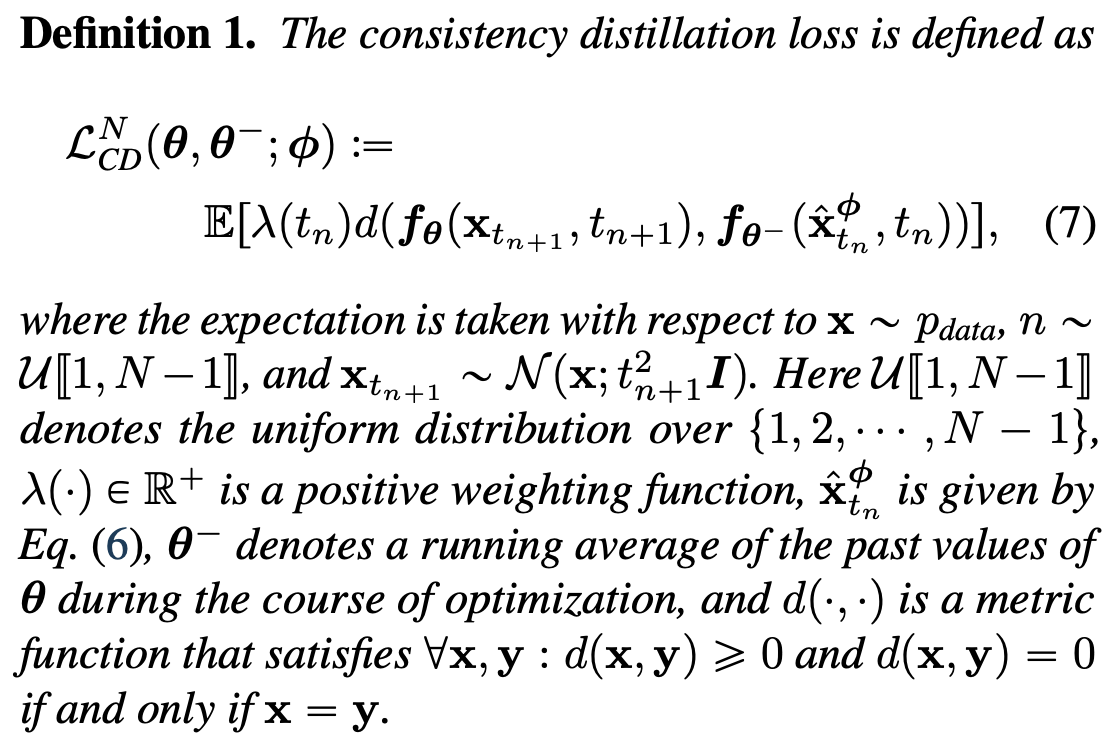
Fig. 494 Consistency Distillation Loss

여기서 metric function \(d(\cdot,\cdot)\) 로는 L1 distance, L2 distance, 그리고 LPIPS distance 를 사용하였고, 실험적으로 확인해본 결과 \(\lambda(t_n) \equiv 1\) 를 적용했을 때 모델 성능이 가장 좋은 부분을 확인할 수 있었다고 합니다. 파라미터 \(\theta\) 는 stochastic gradient descent 그리고 \(\theta^-\) 는 exponential moving average (EMA) 로 학습하였다고 합니다.

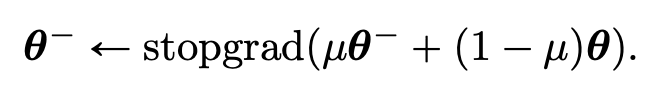
Fig. 495 Exponential Moving Average (EMA)

이처럼 EMA update 와 stopgrad operator 로 학습할 시, \(\theta = \theta^{-}\) 로 설정할때보다 모델을 더 안정적으로 학습할 수 있고 성능에도 개선이 있었다고 합니다. 전체적인 학습 절차는 하단의 Algorithm 2 처럼 정리할 수 있습니다.

Fig. 496 Overview of Consistency Distillation (CD)

\(\theta^{-}\) 는 과거 \(\theta\) 에 대한 running average 이므로 Algorithm 2 가 수렴할 시 이 둘은 일치하게 됩니다. 즉, target network \(f_{\theta^-}\)와 online network \(f_{\theta}\) 가 일치하게 됩니다.

5. Training Consistency Models in Isolation

Consistency Distillation 방식에서는 ground truth score function \(\nabla \log p_t(x_t)\) 을 근사하는 사전학습된 score model \(s_{\phi}(x,t)\) 에 의존했다면, 이에 의존하지 않고 다음과 같은 \(\nabla \log p_t(x_t)\) 에 대한 unbiased estimator 를 활용할 수도 있습니다. 다시 말해, \(-(x_t - x)/t^2\) 로 \(\nabla \log p_t(x_t)\) 를 근사할 수 있습니다.

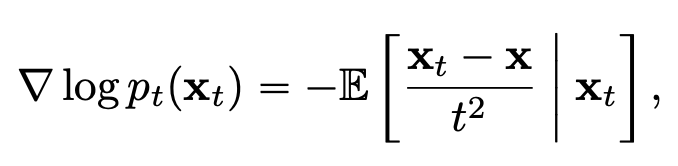
Fig. 497 Unbiased Estimator of Score Function

• \(x \sim p_{data}, x_t \sim N(x; t^2I)\)

Consistency Training (CT) Loss 는 다음과 같이 정의하고, 이는 사전학습된 diffusion model 파라미터 \(\phi\) 와는 독립적인 사실을 확인할 수 있습다.

\[ L_{CT}^{N}(\theta,\theta^{-}) = \mathbb{E}[\lambda(t_n)d(f_{\theta}(x + t_{n+1}z, t_{n+1}), f_{\theta^-}(x+t_nz, t_n))] \]

• \(x \sim p_{data}, n \sim \mathbb{U}[[1,N-1]], x_{t_{n+1}} \sim N(x;t^2_{n+1}I), z \sim N(0,I)\)

• Consistency Training Loss 를 위와 같이 정의하게 된 배경은 다음과 같습니다.

  

  Fig. 498 Consistency Training Loss

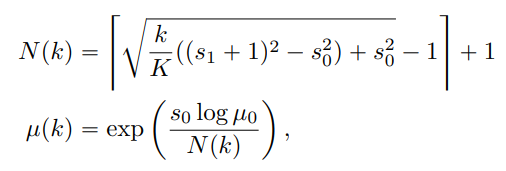
Fig. 499 Schedule Functions for Consistency Training

논문에서 추가적인 성능 개선을 위해 \(N\) 을 점진적으로 증가시키는 방식을 제안합니다. \(N\) 이 작을수록 (\(i.e., \Delta t\) 가 클수록) consistency training loss 가 consistency distillation loss 와 비교했을때 variance 는 감소하지만 bias 는 증가하게 되어, 초기에 더 빠른 convergence 에 이르는데 용이합니다. 반면에, \(N\) 이 클수록 (\(i.e., \Delta t\) 가 작을수록) variance 는 증가하고 bias 는 감소하게 되어, 학습의 마지막 단계에 적용하는 것이 바람직하다고 제안합니다. EMA decay rate schedule function \(\mu(\cdot)\) 도 \(N\) 에 따라 바뀌는 함수로 최종적으로 정의합니다. 전체적인 학습 절차는 하단의 Algorithm 3 처럼 정리할 수 있습니다.

Fig. 500 Overview of Consistency Training (CT)

6. Experiments

논문에서 CIFAR-10, ImageNet 64x64, LSUN Bedroom 256x256, 그리고 LSUN Cat 256x256 데이터셋에 consistency distillation, consistency training 두 학습 방식을 모두 실험하였고, 모델 성능 지표는 FID, IS, Precision, 그리고 Recall 을 사용하였습니다. 모델 architecture 는 CIFAR-10 데이터셋에는 NCSN++, 그리고 그 외 데이터셋에는 ADM 모델을 사용하였습니다.

6.1. Training Consistency Models

CIFAR-10 데이터셋에 다음과 같은 hyperparameter tuning 작업을 진행하였습니다. (metric function \(d(\cdot,\cdot)\), ODE solver, CD (Consistency Distillation) 에서의 number of discretization steps \(N\), 그리고 CT (Consistency Training)) 에서의 schedule functions \(N(\cdot), \mu(\cdot)\))

Parameter Initialization

모델 초기 파라미터 값은 다음과 같이 설정하였습니다.

• Consistency Distillation - 사전학습된 diffusion model 파라미터 값

• Consistency Training - Random Initialization

Results

모델 실험 결과를 다음과 같이 정리할 수 있습니다.

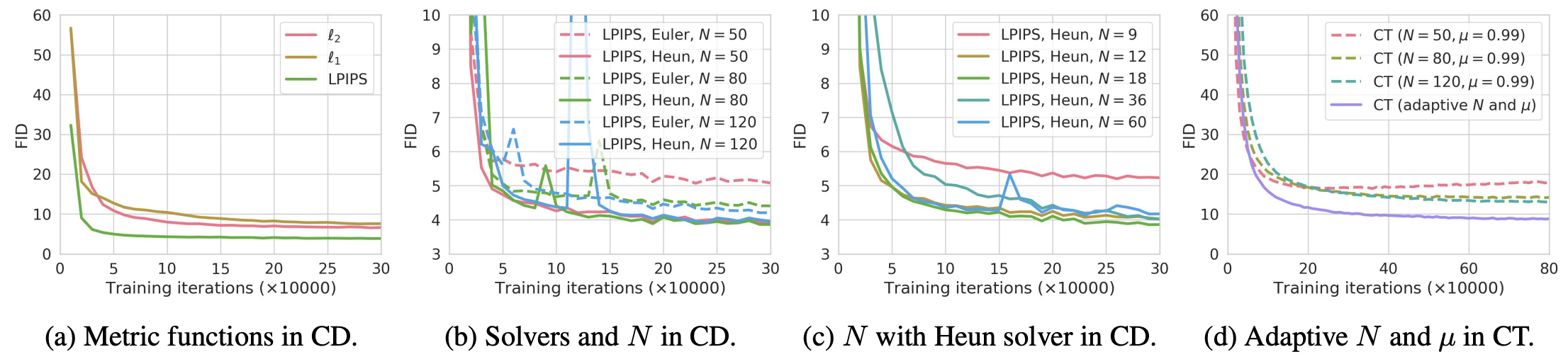
Fig. 501 Experimental Results - Hyperparameters

• Consistency Distillation (CD)

  • LPIPS 를 metric function 으로 사용했을때 모델 성능이 가장 좋았고, 이는 LPIPS metric 이 CIFAR-10 와 같은 natural image 들 간의 유사도를 측정하는데 특화되어 있기 때문이라고 합니다.

  • Euler ODE solver 보다 Heun ODE solver 를 사용했을 때, 그리고 \(N = 18\) 로 설정했을때 모델 성능이 가장 좋았습니다. 또한, 동일한 \(N\) 에 대해서 Heun’s second ode solver 를 사용했을때 Euler’s first ode solver 를 사용했을 때보다 모델 성능이 우월한 부분을 확인할 수 있었다고 합니다.

  이외에도 다른 데이터셋에 hyperparameter tuning 작업을 별도로 진행하였습니다.

• Consistency Training (CT)

  • CD 와 동일하게 LPIPS metric function 사용하였고, ODE solver 는 사용하지 않았습니다.

  • \(N\) 이 작을수록, 모델이 더 빨리 수렴하지만 생성된 이미지 퀄리티는 좋지 않은 부분을 재차 확인할 수 있습니다. (and vice versa)

  • \(N\) 을 점차적으로 증가시키면서 \(\mu\) 도 변화시켰을때 성능이 가장 좋았습니다.

6.2. Few-Step Image Generation

Distillation

논문에서는 Consistency Distillation 모델의 성능을 synthetic data generation 을 필요하지 않는 knowledge distillation 기법 (PD, Salimans & Ho (2022)) 과 다음과 같이 비교합니다.

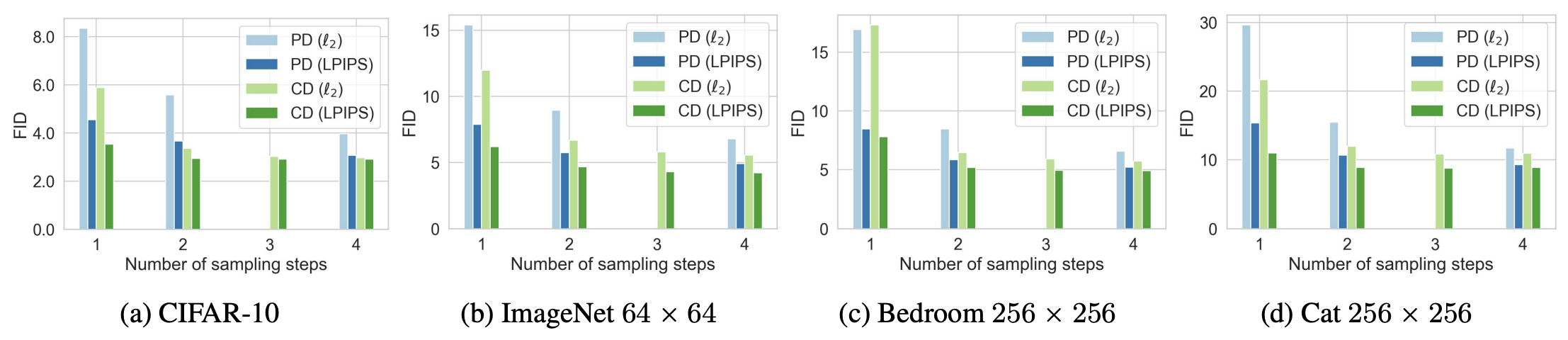
Fig. 502 Experimental Results - Distillation

Direct Generation

CIFAR-10 데이터셋 기준으로 VAE, normalizing flow 를 비롯한 타 single-step generative model 보다 CT 가 성능이 가장 좋았습니다. 또한, distillation 기법 없이도 Progressive Distillation (PD, Salimans & Ho (2022)) 와 견줄만한 성능을 가진 부분을 확인할 수 있습니다. 마지막으로 동일한 noise 로부터 높은 structural similarity 를 가진 이미지들을 생성함으로써 self-consistency 성질도 확인할 수 있었다고 합니다.

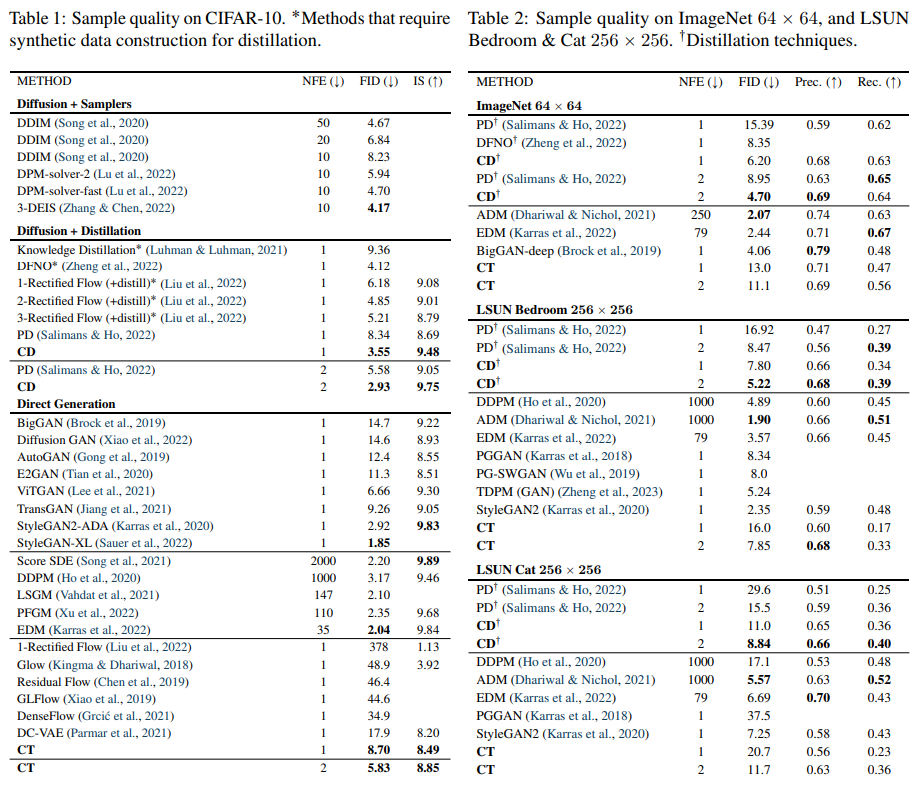
Fig. 503 Experimental Results - Direct Generation

6.3. Zero-Shot Image Editing

Diffusion model 과 유사하게 consistency model 도 multistep sampling 알고리즘을 수정함으로써 zero shot image editing 이 가능합니다. 해당 사진은 LSUN Bedroom 데이터셋에 colorization, super-resolution, stroke-guided image editing task 를 적용한 결과입니다.

Fig. 504 Pseudocode for Zero-Shot Image Editing

Fig. 505 Zero-Shot Image Editing Results