Information
Title: Generative Adversarial Networks (NIPS 2014)
Reference
Author: Sangwoo Jo
Editor: Changhwan Lee
Last updated on Apr. 09, 2024
GAN#
Introduction#
생성형 모델은 크게 생성하고자 하는 데이터의 explicit density 와 implicit density 를 계산하는 방식으로 나뉩니다. Explicit density 를 계산한다는 것은 데이터 분포를 명확하게 사전에 정의하고 모델을 학습하는 것을 의미합니다. 이때, 데이터의 분포를 직접적인 계산이 가능한 tractable density 로 추정하는 방법과 근사화시켜 approximate density 로 추정하는 방법으로 나뉩니다.
Tractable density: AutoRegressive 하게 구하는 방식이 있습니다. AutoRegressive 모델을 사용하여 이전 단계의 데이터를 활용하여 모델을 학습하고, 대표적인 모델로는 PixelCNN, PixelRNN 등이 있습니다.
Approximate density: 대표적으로 score-based model, Boltzmann Machine 등이 있습니다.
Score-based model - 모델 파라미터의 gradient 가 아닌 데이터의 gradient 활용하여 모델을 학습하는 방식으로, energy-based model 에서 MLE 에 사용하는 확률분포를 정규화하는 term 을 따로 계산하지 않아도 되는 장점이 있습니다.
Boltzmann Machine : 완전그래프 구조로 학습하는 생성형 모델입니다. 모델을 학습하는 과정에서 확률 분포의 학습이 어려워(계산량이 많아서 어려움) Markov chain 을 활용하여 학습합니다. 또한, 완전그래프이기 때문에 노드가 늘어날수록 간선, 파라미터 등이 급증하는 문제가 있어 Restricted Boltzmann Machine(RBM) 이 제안되기도 했습니다.
반면에 데이터의 분포를 명확히 정의하지 않고 implicit 하게 모델을 학습하는 방식도 존재합니다. 대표적으로는 Ian Goodfellow 가 2014년에 발표한 GAN 모델이 있습니다. GAN 은 최근에 Diffusion Model 이 소개되기 전까지 몇 년 동안 이미지 생성 분야에서 대표적인 모델로 자리잡았었습니다. GAN 은 VAE 와 달리 marginal likelihood \(p_{\theta}(x)\) 를 직접 구하지 않고, Adversarial Process 를 통해 implicit 하게 샘플링을 해서 분포를 구하게 됩니다.
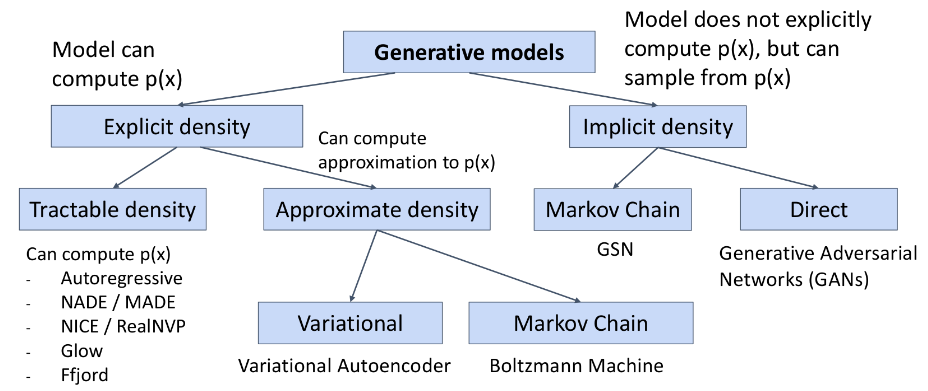
Fig. 8 Taxonomy of Generative Models#
아래 그림과 같이 GAN 은 크게 잠재변수 \(z\) 로부터 가짜 데이터를 생성하는 Generator 와 그로부터 생성된 데이터와 실제 training 데이터를 구분하는 Discriminator 로 구성이 되어 있습니다. 다시 말해서 Discriminator 는 실제 데이터가 들어오면 1, 그리고 가짜로 생성된 데이터가 들어오면 0 을 출력하는 binary classification task 를 진행합니다.
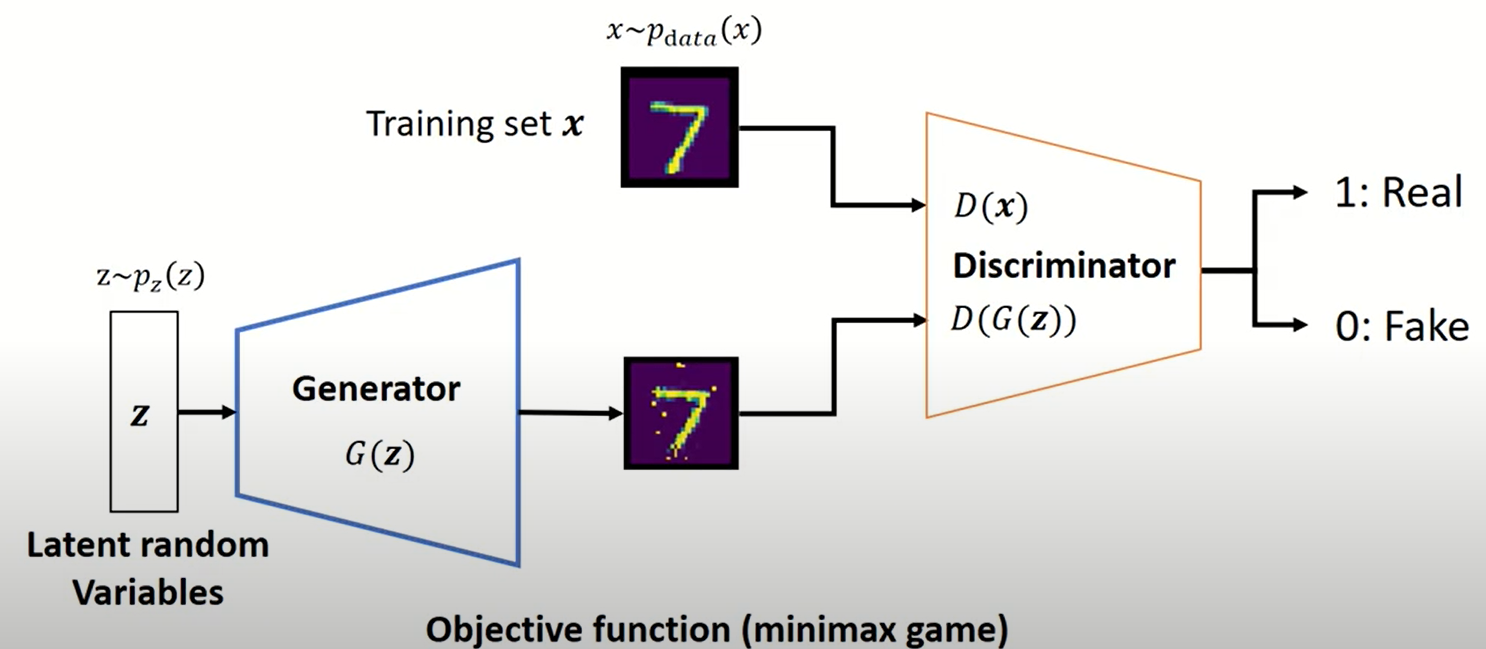
Fig. 9 Generative Adversarial Network(GAN) Architecture#
Generator 와 Discriminator 구현 코드도 같이 살펴보겠습니다.
Generator 구현 code
class Generator(nn.Module): def __init__(self): super(Generator, self).__init__() def block(in_feat, out_feat, normalize=True): layers = [nn.Linear(in_feat, out_feat)] if normalize: layers.append(nn.BatchNorm1d(out_feat, 0.8)) layers.append(nn.LeakyReLU(0.2, inplace=True)) return layers self.model = nn.Sequential( *block(opt.latent_dim, 128, normalize=False), *block(128, 256), *block(256, 512), *block(512, 1024), nn.Linear(1024, int(np.prod(img_shape))), nn.Tanh() ) def forward(self, z): img = self.model(z) img = img.view(img.size(0), *img_shape) return img
Discriminator 구현 code
class Discriminator(nn.Module): def __init__(self): super(Discriminator, self).__init__() self.model = nn.Sequential( nn.Linear(int(np.prod(img_shape)), 512), nn.LeakyReLU(0.2, inplace=True), nn.Linear(512, 256), nn.LeakyReLU(0.2, inplace=True), nn.Linear(256, 1), nn.Sigmoid(), ) def forward(self, img): img_flat = img.view(img.size(0), -1) validity = self.model(img_flat) return validity
Training Procedure#
GAN 을 학습할 시, D를 먼저 최적화하는 k 단계와 G를 최적화하는 한 단계를 번갈아 수행합니다. 그리고 이때 쓰이는 손실함수(loss function)은 다음과 같습니다.
논문에서 제시한 학습 알고리즘과 실제 implementation code 를 비교해보겠습니다.

Fig. 10 Generative Adversarial Network(GAN) Training Procedure#
GAN 학습 code
# ---------- # Training # ---------- for epoch in range(opt.n_epochs): for i, (imgs, _) in enumerate(dataloader): # Adversarial ground truths valid = Variable(Tensor(imgs.size(0), 1).fill_(1.0), requires_grad=False) fake = Variable(Tensor(imgs.size(0), 1).fill_(0.0), requires_grad=False) # Configure input real_imgs = Variable(imgs.type(Tensor)) # ----------------- # Train Generator # ----------------- optimizer_G.zero_grad() # Sample noise as generator input z = Variable(Tensor(np.random.normal(0, 1, (imgs.shape[0], opt.latent_dim)))) # Generate a batch of images gen_imgs = generator(z) # Loss measures generator's ability to fool the discriminator g_loss = adversarial_loss(discriminator(gen_imgs), valid) g_loss.backward() optimizer_G.step() # --------------------- # Train Discriminator # --------------------- optimizer_D.zero_grad() # Measure discriminator's ability to classify real from generated samples real_loss = adversarial_loss(discriminator(real_imgs), valid) fake_loss = adversarial_loss(discriminator(gen_imgs.detach()), fake) d_loss = (real_loss + fake_loss) / 2 d_loss.backward() optimizer_D.step() print( "[Epoch %d/%d] [Batch %d/%d] [D loss: %f] [G loss: %f]" % (epoch, opt.n_epochs, i, len(dataloader), d_loss.item(), g_loss.item()) ) batches_done = epoch * len(dataloader) + i if batches_done % opt.sample_interval == 0: save_image(gen_imgs.data[:25], "images/%d.png" % batches_done, nrow=5, normalize=True)
이렇게 Discriminator 와 Generator 는 각각 \(V(D,G)\) 가 최대화하고 최소화하는 방향으로 stochastic gradient descent 를 진행하게 됩니다. 하지만 아래 그림처럼 실제로 Generator를 학습할 때, 초반에 \(D(G(z)) \approx 0\) 일 경우 학습하지 못하는 상황이 발생합니다. 이 때, \(\log(1-D(G(z))\) 를 최소화하지 않고 \(\log(D(G(z))\) 를 최대화하는 방향으로 Generator 를 학습하는 기법도 있습니다.
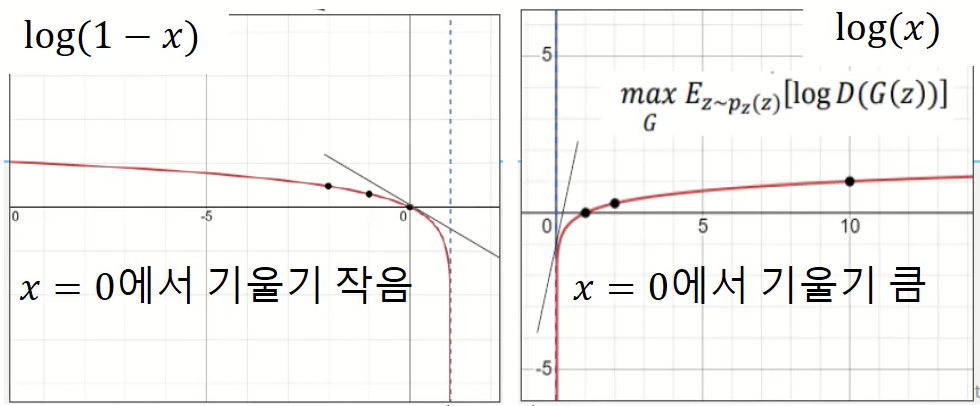
Fig. 11 Alternative to Vanishing Gradient when Training the Generator#
이렇게 학습함으로써 최적화된 solution 에서는 Generator 가 training 데이터 분포를 완벽히 복원하고 Discriminator 는 binary classification 확률을 언제나 1/2 로 내뱉게 됩니다.
Theoretical Results#
Proposition 1. 고정된 Generator 에 대해서, 최적화된 Discriminator 는 다음과 같습니다.
이를 증명하자면, Discriminator 에 대한 손실함수를 다음과 같이 쓸 수 있고 \(D = D_{G}^*(x)\) 가 이를 최대화하는 solution 입니다.
Proposition 2. 최적화된 Discriminator 에 대해 \(\max_D V(D,G)\) 를 최소화하는 Generator 는 \(p_g = p_{data}\) 일때 성립하고 이때 \(D = D_{G}^*(x) = 1/2\) 입니다.
이를 증명하자면, 최적화된 Discriminator 에 대한 손실함수는 다음과 같고
\(KL(p_{data}(x)\ ||\ \frac{p_{data}+p_{g}}{2}) + KL(p_{g}(x)\ ||\ \frac{p_{data}+p_{g}}{2}) = 2\ \cdot\ JSD(p_{data}\ ||\ p_{g})\) 의 최솟값은 0 이고 이는 \(p_g = p_{data}\) 일때 성립합니다.
Experiments#
논문에서 MNIST, the Toronto Face Database(TFD), 그리고 CIFAR-10 dataset 로 모델 실험 및 성능 평가했습니다. 평가시에는 \(p_g\) 로부터 Parzen density estimation을 거쳐 계산한 log likelihood estimate 로 모델 성능 평가를 진행했습니다. 아래 표를 보면 실험 방법 중 GAN이 제일 결과가 좋은 것을 볼 수 있습니다.
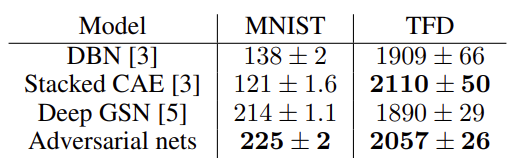
Fig. 12 Experimental Results#
Summary#
VAE는 새로운 데이터를 잘 생성하지만 생성된 이미지가 흐릿하다는 단점을 지니고 있습니다. 반면에 GAN 은 high quality image 를 잘 생성하지만 unstable 한 convergence 를 가지고 있습니다. 그래서 실제로 VAE 는 Encoder 를 활용한 차원축소로 많이 활용되고 이미지 데이터를 생성하는데는 GAN 이 많이 활용되었다고 합니다.
