Information
Title: Diffusion Models already have a Semantic Latent Space (ICLR 2023)
Reference
Author: Sehwan Park
Last updated on Nov. 18, 2023
Diffusion Models already have a Semantic Latent Space#
Abstract#
Diffusion model은 많은 domain에서 좋은 성능을 보이지만 generative process를 control하는 semantic latent space가 부족하다. 논문에서는 diffusion model속에서 semantic latent space를 발견하기 위한 asymmetric reverse process(asyrp)를 제안하고 h-space라고 명칭한 semantic latent space의 좋은 특성(homogeneity, linearity, robustness, consistency across timesteps)들을 보여준다. 추가적으로 editing strength와 quality deficiency를 기준으로 삼고 더 좋은 image-image translation을 위한 Generative Process Design을 소개한다.
1. Introduction#
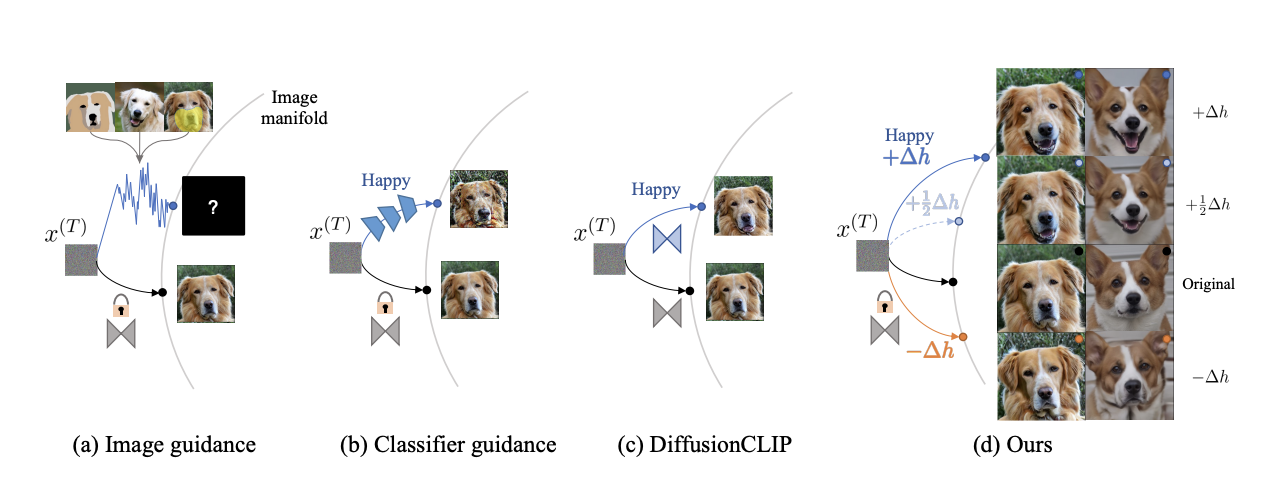
Fig. 431 Manipulation approaches for diffusion models#
(a) Image guidance는 unconditional한 latent variable에 guiding image의 latent variable을 합치는 방식을 사용한다. 그러나 latent variable을 둘 다 이용하면서 명확하게 control하기가 쉽지 않다.
(b) Classifier guidance는 diffusion model에 classifier를 추가하여 generative process를 거치는 동안 latent variable이 어떤 class인지 분류하고 target class에 가까워지도록 score를 부여하는 방식으로 작동한다. 그러나 latent variable들에 대해 classify를 실행해야 하기에 pretrained model을 사용하기가 힘들어 직접 학습을 시켜야 하기에 시간적으로, 비용적으로 부담이 된다.
(c) DiffusionCLIP
(d) Diffusion Models already have a Semantic Latent Space는 original image의 특성을 edit하기 위한 아주 좋은 특성을 가지고 있는 semantic latent space를 frozen diffusion model에서 발견하였고 이를 h-space라고 칭한다. h-space에는 다양한 좋은 특성들이 존재한다. versatile editing과 quality boosting을 위해 새로운 generative process를 design하여 제안한다. h-space는 frozen pretrained diffusion model에서 semantic latent space로써의 첫 발견사례이다.
2. Background#
2.1 Denoising Diffusion Probability Model(DDPM)#
DDPM에서는 임의의 time step t로 부터 noise가 껴있는 image \(x_t\)의 \(\epsilon_t\)가 얼만큼인지 예측한다. 예측한 \(\epsilon_t\)를 이용하여 noise가 일부 제거된 이전 step의 mean(\(\mu_{\theta}(x_t)\))을 구할 수 있고 variance(\(\sum_{\theta}(x_t)\))는 constant한 값으로 고정시킨다. DDPM에서 제시한 forward process와 reverse process는 다음과 같다. DDPM에서의 \(\sigma_t^2 = \beta_t\)이다.
2.2 Denoising Diffusion Implicit Model(DDIM)#
DDIM에서는 non-Markovian process를 이용해 또 다른 관점의 reverse process를 제시하였고, DDPM과 DDIM 모두 general하게 적용되는 Diffusion process에 대한 식을 보여주었다. \(\sigma_t = \eta\sqrt{(1-\alpha_{t-1}) / (1-\alpha_t)} \sqrt{1-\alpha_t/\alpha_{t-1}}\)이다.
\(\eta\)=1인 경우 DDPM이 되고 stochastic해지며, \(\eta\)=0인 경우 DDIM이 되고 deterministic해진다.
2.3 Image Manipulation with CLIP#
CLIP은 Image Encoder와 Text Encoder를 이용하여 image와 text간의 embedding을 학습한다. 편집된 이미지와 대상 설명 간의 cosine distance를 직접 최소화하는 대신 cosine distance를 사용한 directional loss를 사용하여 mode collapse없이 균일한 editing을 가능하게 했다고 한다.
\(\Delta T = \mathrm{E}_T(y^{target}) - \mathrm{E}_T(y^{source}) \)
\(\Delta I = \mathrm{E}_I(x^{edit}) - \mathrm{E}_I(x^{source})\)
3. Discovering Semantic Latent Space In Diffusion Models#
Editiing을 하는 과정에서 naive approach를 통해서는 editing이 잘 이루어지지 않는다. 이 chapter에서는 왜 잘 이루어지지 않는지에 대한 설명을 하고 이를 해결하는 새로운 controllable한 한 reverse process인 Asymmetric Reverse Process(Asyrp)를 제안한다.
DDIM에서 \(x_{t-1}\)에 대한 수식을 설명하였는데 이 chapter부터는 “predicted \(x_0\)”부분을 \(\mathrm{P}_t(\epsilon_t^{\theta}(x_t))\) 즉 \(\mathrm{P}_t\)라고 설정하고, “direction pointing to \(x_t\)”부분을 \(\mathrm{D}_t(\epsilon_t^{\theta}(x_t))\) 즉 \(\mathrm{D}_t\)라고 설정하였다.
\(\mathrm{P}_t\)는 latent variable로 부터 \(x_0\)를 예측하는 reverse process와 같은 역할을 담당하고 \(\mathrm{D}_t\)는 다시 noise를 추가해 latent variable로 돌아가기에 forward process와 같은 역할을 담당한다.
3.1 Problem#
\(x_T\)로 부터 생성된 image \(x_0\)를 given text prompts에 맞게 manipulate시키는 가장 간단한 방법은 2.3에서 소개한 \(\mathcal{L}_{direction}\)을 optimize하도록 \(x_T\)를 update하는 것이다. 하지만 이 방법은 distorted images를 생성하거나 부정확한 manipulation을 한다고 한다.
이에 대한 대안으로, 모든 sampling step에서 원하는 방향으로 manipulate하도록 \(\epsilon_t^{\theta}\)를 shift해주는 방법이 제시되었다. 하지만 이 방법은 \(x_0\)를 완전히 manipulate하지 못한다. 왜냐하면 \(\mathrm{P}_t\)와 \(\mathrm{D}_t\)에서 둘다 shifted된 \(\tilde{\epsilon}_t^{\theta}\)를 사용하기에 cancel out되어 결국 latent variable에서는 기존과 다름이 없다는 것이다. 자세한 증명은 Proof of Theroem을 보면 된다.
Proof of Theroem)
Define \(\alpha_t = \prod_{s=1}^t(1 - \beta_s)\), \(\tilde{x}_{t-1} = \sqrt{\alpha_{t-1}}\mathrm{P}_t(\tilde{\epsilon}_t^{\theta}(x_t)) + \mathrm{D}_t(\tilde{\epsilon}_t^{\theta}(x_t)) + \sigma_t\mathcal{z_t}\)
= \(\sqrt{\alpha_{t-1}}\underbrace{\bigg(\cfrac{x_t - \sqrt{1-\alpha_t}(\epsilon_t^\theta(x_t) + \Delta \epsilon_t)}{\sqrt{\alpha_t}}\bigg)}_{\mathrm{P}_t(\tilde{\epsilon}_t^{\theta})} + \underbrace{\sqrt{1-\alpha_{t-1}-\sigma_t^2}\cdot (\epsilon_t^\theta(x_t) + \Delta \epsilon_t) }_{\mathrm{D}_t(\tilde{\epsilon}_t^{\theta})} + \sigma_t\mathcal{z_t}\)
= \(\sqrt{\alpha_{t-1}}\mathrm{P}_t(\epsilon_t^\theta(x_t)) + \mathrm{D}_t(\epsilon_t^\theta(x_t)) - \cfrac{\sqrt{\alpha_{t-1}}\sqrt{1-\alpha_t}}{\sqrt{\alpha_t}} \cdot \Delta \epsilon_t + \sqrt{1-\alpha_{t-1}} \cdot \Delta \epsilon_t\)
\(\sqrt{\alpha_{t-1}}\mathrm{P}_t(\epsilon_t^\theta(x_t)) + \mathrm{D}_t(\epsilon_t^\theta(x_t))\)는 기존 DDIM에서의 \(x_{t-1}\)에 대한 식이고 위 식의 \(\Delta \epsilon_t\)항만 따로 묶어서 표현하면 아래와 같다.
= \(x_{t-1} + \bigg( -\cfrac{\sqrt{1-\alpha_t}}{\sqrt{1-\beta_t}} + \sqrt{1-\alpha_{t-1}} \bigg) \cdot \Delta \epsilon_t \)
= \(x_{t-1} + \bigg( -\cfrac{\sqrt{1-\alpha_t}}{\sqrt{1-\beta_t}} + \cfrac{\sqrt{1-\prod_{s=1}^{t-1}(1-\beta_s)}\sqrt{1-\beta_t}}{\sqrt{1-\beta_t}} \bigg) \cdot \Delta \epsilon_t \)
\({\sqrt{1-\prod_{s=1}^{t-1}(1-\beta_s)}\sqrt{1-\beta_t}}\)를 root를 묶어서 내부를 계산하면 \(\sqrt{1-\alpha_t-\beta_t}\)이므로 정리하면 아래와 같다.
= \(x_{t-1} + \bigg( \cfrac{\sqrt{1-\alpha_t-\beta_t} - \sqrt{1-\alpha_t}}{\sqrt{1-\beta_t}} \bigg) \cdot \Delta \epsilon_t \)
\(\therefore \Delta x_t = \tilde{x_{t-1}} - x_{t-1} = \cfrac{\sqrt{1-\alpha_t-\beta_t} - \sqrt{1-\alpha_t}}{\sqrt{1-\beta_t}} \bigg) \cdot \Delta \epsilon_t\)
shifted epsilon을 사용한 결과이다. 분자를 보면 \(\beta_t\)는 매우 작기에 거의 0에 수렴하기에 결국 차이가 거의 없음을 보인다.
즉 \(\epsilon\)-space에서의 manipulation 효과는 매우 좋지 않음을 알 수 있다.

Fig. 432 No Manipulation Effect with shifted epsilon#
3.2 Asymmetric Reverse Process(Asyrp)#
chapter 3.1에서 \(\epsilon\)-space에서의 문제를 해결하기 위해 저자들은 Asyrp를 제안한다. 이름 그대로 비대칭적인 방법을 사용한다는 것인데 \(x_0\)를 예측하는 \(\mathrm{P}_t\)에서는 shifted epsilon을 사용하고, latent variable로 돌아가는 \(\mathrm{D}_t\)에서는 non-shifted epsilon을 사용해서 전체적인 변화를 준다는 것이다. 즉, \(\mathrm{P}_t\)만modify하고 \(\mathrm{D}_t\)는 유지한다. Asyrp를 식으로 표현하면 다음과 같다.
Loss식 또한 chapter 2.3에서 제시한 \(\mathcal{L}_{direction}\)을 사용하여 재구성하였다. modify를 하지 않은 \(\mathrm{P}_t^{source}\)와 modifiy를 한 \(\mathrm{P}_t^{edit}\)을 사용한다. Loss식은 다음과 같다.
전체적인 reverse process는 다음과 같이 설계가 되었다. 이제 shifted epsilon인 \(\tilde{\epsilon}_t^{\theta}(x_t)\)를 어떤 방식으로 얻을 것인지에 대한 설계가 필요하다. 저자들은 기존의 \(\epsilon\)-space에서 변화를 주는 것보다 훨씬 더 좋은 result를 보이고, nice properties를 가지는 h-space에서 변화를 주는 것을 제안한다.
3.3 h-space#
\(\epsilon_t^{\theta}\)는 diffusion models의 backbone인 U-Net에서 도출된다. 이 논문에서는 Image manipulation을 위해 \(\epsilon_t^{\theta}\)를 control하는 space를 U-Net의 bottleneck 즉, 가장 깊은 feature map인 \(h_t\)로 정하였다. 이를 h-space라고 부른다. h-space는 \(\epsilon\)-space보다 더 작은 spatial resolutions을 가지고 high-level semantic를 가진다. 또한 \(\epsilon\)-space에서는 발견할 수 없는 매우 nice한 특성들을 가지고 있다.
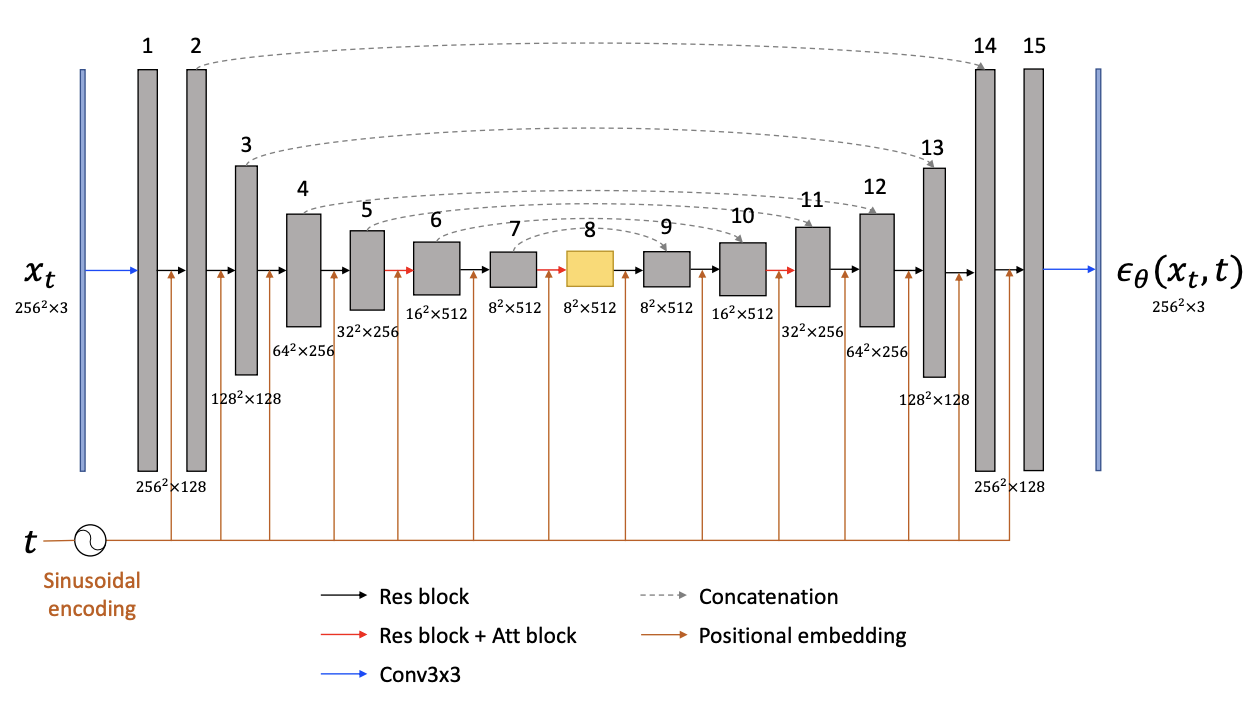
Fig. 433 U-Net structure and h-space#
h-space의 크기는 \(8^2\times512\)이고 \(\epsilon\)-space의 크기는 \(256^2\times3\)으로 h-space에서의 control이 더 지배적이고 robust함을 추측할 수 있다(실제 실험적으로 증명을 함). h-space는 skip-connection의 영향을 받지 않으며 가장 압축된 정보를 가지고 있는 공간이며 image를 control하는데에 있어 매우 좋은 특성들을 가지고 있다. 실제 저자들은 h-space를 지정하기 위해 U-Net의 모든 feature map을 h-space로 설정해두고 실험을 해보았는데 위의 그림을 기준으로 8th layer이전의 feature map을 h-space로 지정한 경우에는 manipulaton이 적게 이루어졌고, 8th layer 이후의 feature map을 h-space로 지정한 경우에는 너무 과한 manipulation이 이루어지거나 아예 distorted image가 생성되었다. h-space만의 특성은 chapter5에서 설명한다.
3.4 Implicit Neural Directions#
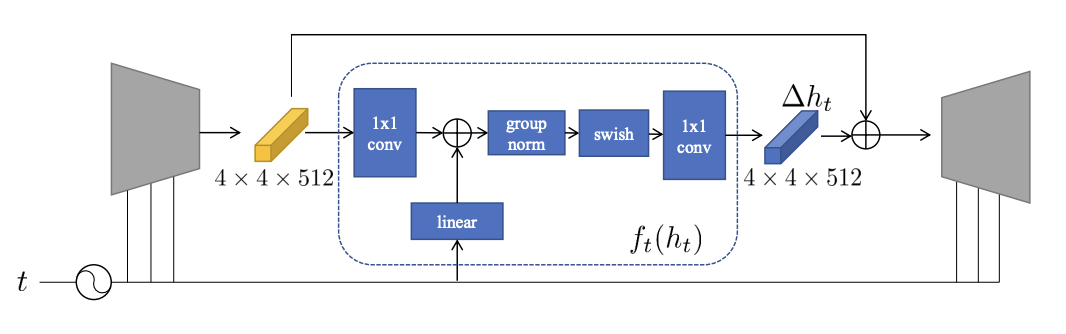
Fig. 434 Illustration of \(\mathrm{f}(t)\)#
\(\Delta h_t\)가 image를 manipulating하는데 성공했음에도, 수많은 timestep에서 매번 optimizing하기란 쉽지 않다. 대신에 논문에서는 \(h_t\)를 입력받아 \(\Delta h\)를 출력해주는 작은 neural network인 \(\mathrm{f}(t)\)를 추가하였다. \(\mathrm{f}(t)\)는 \(\Delta h_t\)를 매번 모든 timestep에서 optimizing해줘야 하는 방법에 비해 시간도 빠르고 setting값들에 대해 robust하다. 또한 주어진 timestep과 bottleneck feature인 \(h_t\)에 대해 \(\Delta h_t\)를 출력하는 방법을 학습하기에 unseen timestep과 bottleneck feature에 대해서도 일반화할 수 있다고 한다. 이는 accelerated한 과정에서도 큰 효과를 본다. training scheme이 어떻든 간에 결국 부여하는 \(\sum\Delta\mathrm{h_t}\)만 보존된다면, 어떠한 length를 설계해도 비슷한 manipulation효과를 볼 수 있다.
h-space에서 epsilon을 control해서 asyrp 이용하는 식은 다음과 같다. 이해를 위해 \(\epsilon\)-space와 h-space에서의 shifted epsilon \(\tilde{\epsilon}_t^{\theta}(x_t)\)을 비교하였다.
\(\epsilon\)-space에서의 shifted epsilon
\(\tilde{\epsilon}_t^{\theta}(x_t) = \epsilon_t^{\theta}(x_t) + \Delta \epsilon_t\)
h-space에서의 shifted epsilon
\(\tilde{\epsilon}_t^{\theta}(x_t) = \epsilon_t^{\theta}(x_t | \Delta h_t)\)
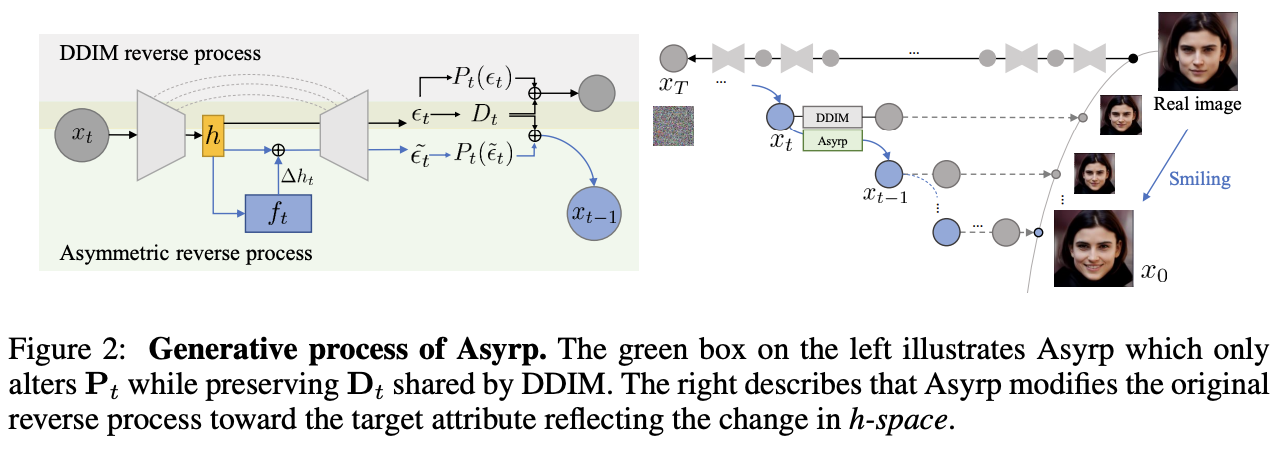
Fig. 435 Asymmetric Reverse Process#
4. Generative Process Design#

Fig. 436 Intuition for choosing the intervals for editing and quality boosting#
Perception prioritized training of diffusion models(Choi et al)에서는 Diffusion model이 early stage에서는 high-level context를 generate하고, later stage에서는 imperceptible fine details를 generate한다고 제안한다. 본 논문에서는 early stage에서 editing을 진행하는 editing process와 later stage에서 imperceptible fine details를 진행하는 quality boosting을 위한 구간을 나눠서 새로운 Generative Process Design을 제시한다.
4.1 Editing Process With Asyrp#
Editing Process에서는 high-level context가 generate되어야 하므로 전체 timestep[0,T]에서 Editing Process를 위한 editing interval을 [T, \(t_{edit}\)]으로 설정하였다. \(t_{edit}\)의 시점을 결정하기 위해 LPIPS 측정지표를 이용한다. LPIPS(\(\mathrm{x}, \mathrm{P}_t\))는 t시점에서 예측한 \(x_0\)와 target이 되는 original image간의 perceptual distance를 계산한다. 따라서 LPIPS를 남은 reverse process을 통해 editing 해야 할 구성요소를 측정하는 지표라고 볼 수도 있다. 첫 step T의 LPIPS로 부터 \(t_{edit}\)시점에서의 LPIPS 차이는 Editing Process에서 얼만큼의 perceptual change를 주었는지를 나타낸다. 이 값을 editing strength(\(\epsilon_t\))라고 정의한다.
Editing interval이 작으면 \(\xi_t\)가 작아지며 변화가 많이 일어나지 않고 반면, Editing interval이 크면 \(\xi_t\)가 커지고 변화가 많이 일어난다. 따라서 충분한 변화를 줄 수 있는 한에서 가장 최소의 Editing interval을 찾는 것이 \(t_{edit}\)을 결정하는 최고의 방법이다. 저자들은 실험적인 결과를 통해 \(\mathrm{LPIPS}(x, \mathrm{P}_t)\) = 0.33인 t시점을 \(t_{edit}\)으로 결정하였다.

Fig. 437 Results based on various \(\mathrm{LPIPS}(x, \mathrm{P}_{t_{edit}})\)#

Fig. 438 Importance of choosing proper \(t_{edit}\)#
몇몇 특성들은 다른 특성들에 비해 visual change를 많이 필요로 하는 경우도 있다. 예를 들어 source image에 대해 smile한 attribute를 추가하는 경우보다 pixar style의 attribute을 추가하는 경우가 더 많은 visual change를 필요로 한다. 이러한 경우에는 Editing interval을 더 길게 설정해야 한다. 이러한 경우에는 \(\mathrm{LPIPS}(x, \mathrm{P}_t)\) = 0.33 - \(\delta\)를 만족하는 t를 \(t_{edit}\)으로 설정한다. 이 때, \(\delta = 0.33d(\mathrm{E}_T(y_{source}), \mathrm{E}_T(y_{target}))\)이다. \(\mathrm{E}_T\)는 CLIP text embedding을 진행하는 Text Encoder를 의미하며, d는 cosine distance를 의미한다. 아래 그림을 통해 더 많은 visual change를 요구하는 attributes에 대해서는 \(t_{edit}\)이 더 작음(Editing Interval이 김)을 알 수 있다.
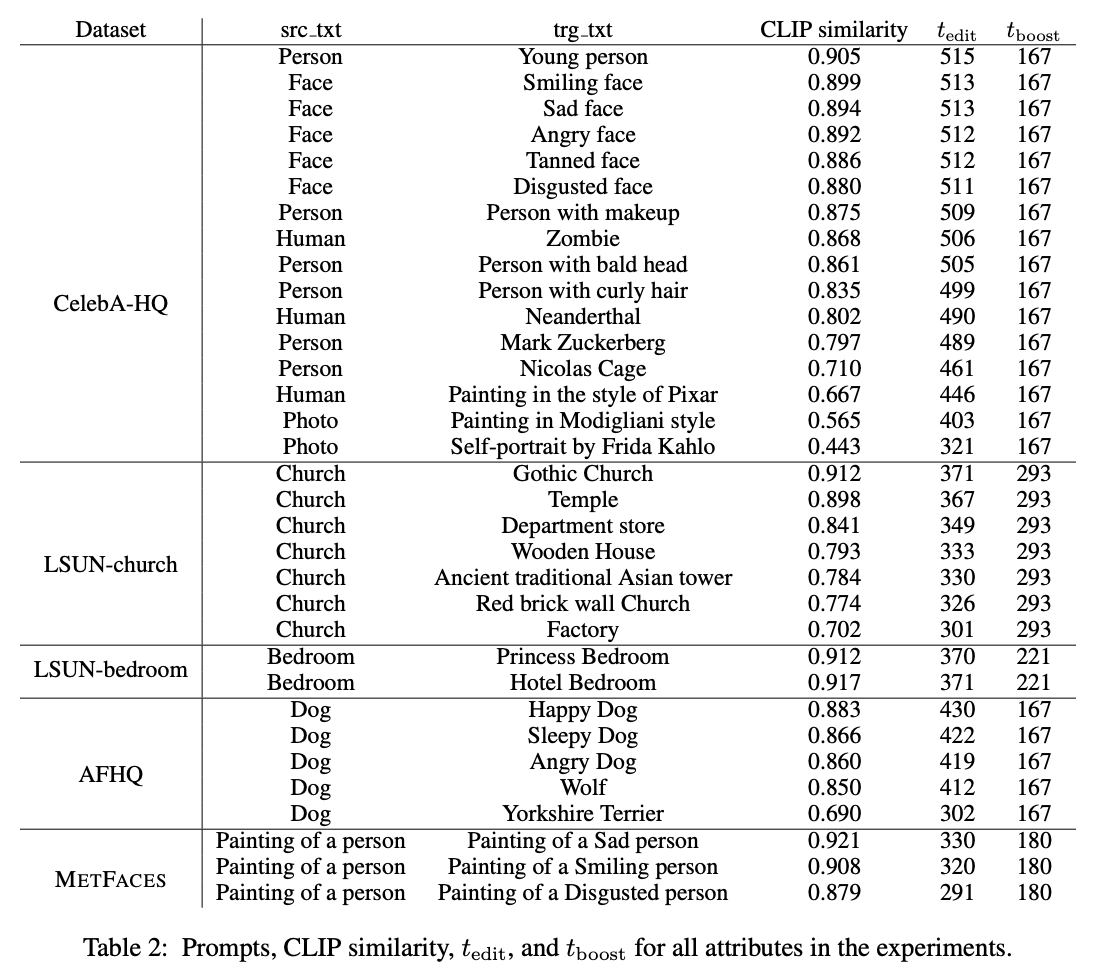
Fig. 439 Flexible \(t_{edit}\) based on the amount of visual changes.#
4.2 Quality Boosting With Stochastic Noise Injection#
DDIM은 \(\eta\)=0으로 설정하며 stochasticity를 제거하여 거의 완벽한 inversion을 가능케 하였다. Elucidating the design space of diffusionbased generative models(Karras et al.)에서는 stochasticity가 image quality를 증가시킨다고 증명하였다. 이에 따라 본 논문에서는 Generative Process에 stochastic noise를 주입하는 quality boosting 단계를 설정하고 boosting interval은 [\(t_{boost}\), 0]이다.
Boosting Interval에 따라 image quality를 control할 수 있는데, Boosting Interval이 길게되면, Quality는 증가하지만 Interval동안 계속해서 stochastic noise를 주입해야 하기에 content가 변하는 문제가 발생할 수도 있다. 따라서 충분한 quality boosting을 달성하면서도 content에 최소한의 변화만을 줄 수 있도록 \(t_{boost}\)를 설정하는 것이 중요하다. 저자들은 image에 껴있는 noise를 quality boosting을 통해 해결해야 할 부분으로 보았으며 target이 되는 original image로 부터 t시점의 image \(x_t\)에 얼만큼의 noise가 껴있는지에 대한 지표로 quality deficiency \(\gamma_t\)를 이용한다.
여기서는 editing strength와는 다르게 time step에 따라 예측한 \(x_0\)인 \(\mathrm{P}_t\)가 아닌 latent variable \(x_t\)를 이용한다. 저자들은 noise를 판단하는데에 있어서 semantics보다는 actual image를 고려했기에 위와 같이 설정하였다고 한다. 저자들은 실험적인 결과를 통해 \(\gamma_t\) = 1.2인 t시점을 \(t_{boost}\)로 설정하였다.
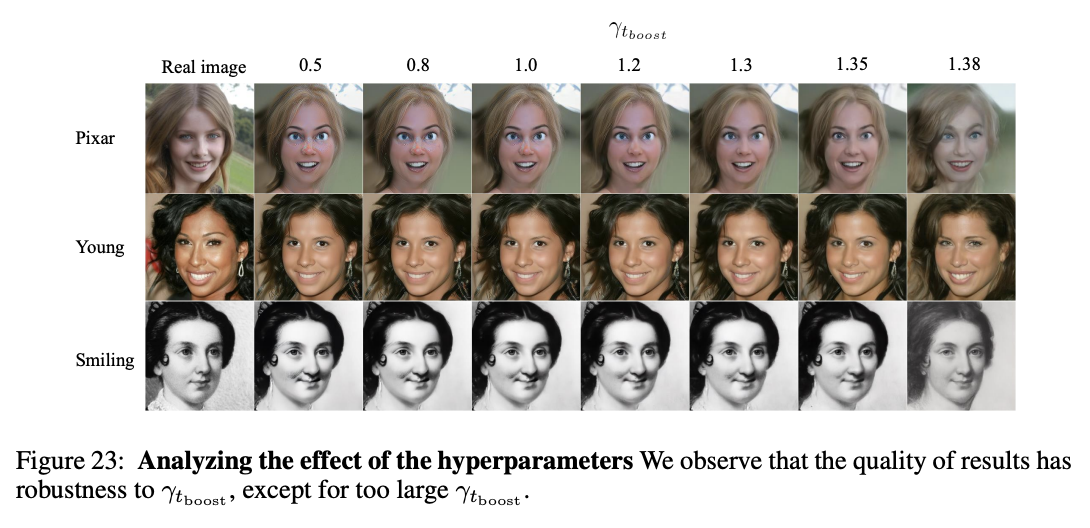
Fig. 440 Results based on various \(\gamma_{t_{boost}}\)#

Fig. 441 Quality comparison based on the presence of quality boosting#
4.3 Overall Process of Image Editing#
General한 Diffusion model에서의 Generative Process를 표현하면 다음과 같다.
\(\eta\) = 0인 경우에는 DDIM이 되며, stochastic noise를 더하는 부분이 사라져 deterministic해진다. \(\eta\) = 1인 경우에는 DDPM이 되며, stochastic한 특성이 있다. Asyrp(Assymetric Reverse Process)에서는 기본적으로 DDIM을 사용하며 \(\mathrm{P}_t\)에서 h-space를 통해 control된 \(\epsilon_t^{\theta}(x_t|f_t)\)를 사용한다. Diffusion Models already have a Semantic Latent Space에서 제시한 Generative Process를 전체적으로 정리하면 다음과 같다.
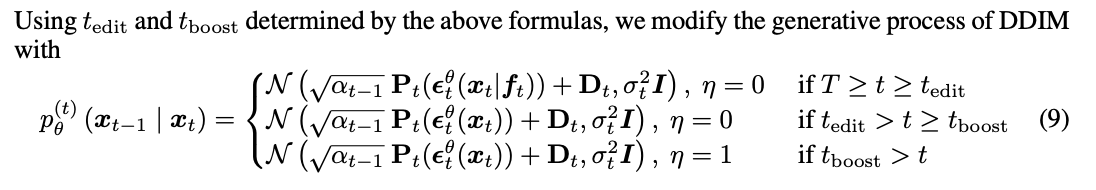
Fig. 442 Quality comparison based on the presence of quality boosting#
처음부터 \(t_{edit}\)시점까지는 Asyrp를 이용해 Editing Process를 진행한다. 이 후 DDIM 방식을 통해 Denoising을 진행하다가 \(t_{boost}\)시점부터 끝날 때까지 stochastic noise를 주입하는 DDPM 방식을 이용해 Quality boosting을 진행한다.
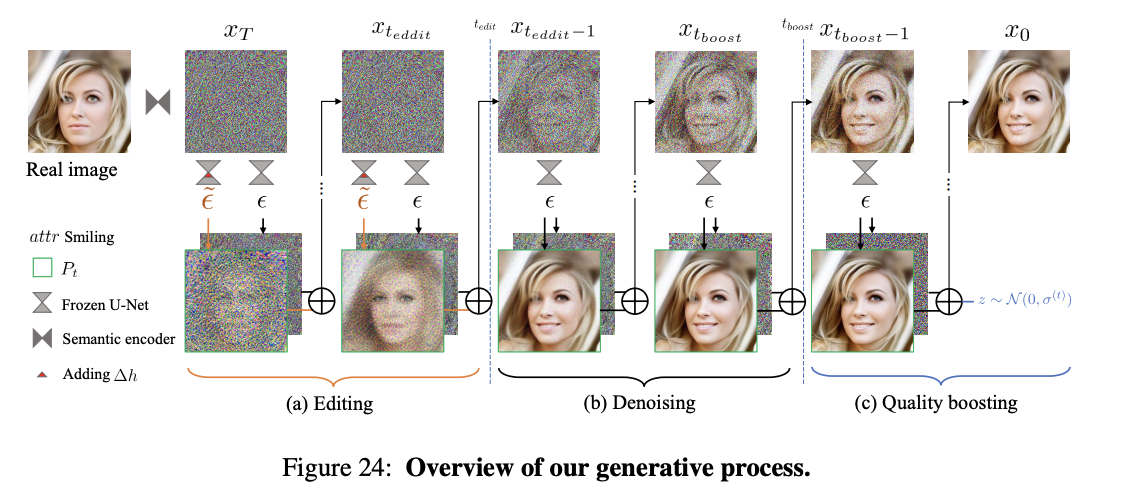
Fig. 443 Overview of Generative Process#
5. Experiments#
CelebA-HQ (Karras et al., 2018) 및 LSUN-bedroom/-church (Yu et al., 2015) 데이터셋에서 DDPM++ (Song et al., 2020b) (Meng et al., 2021); AFHQ-dog (Choi et al., 2020) 데이터셋에서 iDDPM (Nichol & Dhariwal, 2021); 그리고 METFACES (Karras et al., 2020) 데이터셋에서 ADM with P2-weighting (Dhariwal & Nichol, 2021) (Choi et al., 2022)을 사용해 각각 학습시켰다고 한다. 모든 model들은 pretrained checkpoint를 활용했으며 frozen상태를 유지시켰다고 한다.
5.1 Versatility of h-space with Asyrp#

Fig. 444 Editing results of Asyrp on various datasets#
위의 그림을 보면, 논문에서는 다양한 attribute들의 특성을 잘 반영해서 image를 manipulate했다는 점을 알 수 있다. 심지어 {department, factory, temple} attribute은 training data에 포함이 되어있지 않았음에도 성능이 잘 나온 점을 확인할 수 있다. model을 fine tuning하지 않고 inference하는 과정에서 h-space를 통해 epsilon을 control하고 Asyrp를 이용해 성능을 냈다는 점이 가장 큰 장점이다.
5.2 Quantitive Comparison#
Asyrp model의 결과를 다른 model들과 비교하는 실험을 진행하였는데 diffusion model 전체를 fine-tuning하여 image을 editing하는 DiffsionCLIP model과 비교하였다. Asyrp의 성능이 더 좋음을 확인 할 수 있다.

Fig. 445 Asyrp vs DiffusionCLIP on both CelebA-HQ seen-domain attributes and unseen-domain attributes#
5.3 Analysis on h-space#
Homogeneity

Fig. 446 Homogeneity of h-space#
위의 그림의 (a)는 Real image에 smiling attribute을 추가하기 위해 최적화된 \(\Delta h_t\)와 \(\Delta \epsilon_t\)를 나타낸다. 같은 값을 다른 Real image에 적용시켰을 때의 결과를 (b)에 나타내었는데, \(\Delta h_t\)를 적용한경우 smiling face로 잘 바뀌는 반면, \(\Delta \epsilon_t\)을 적용한 경우에는 image distortion이 발생함을 알 수 있다.
Linearity

Fig. 447 Linearity of h-space - Linear Scaling#
\(\Delta_h\)를 linearly scaling을 하는 것은 editing을 하는데에 있어 visual attribute change의 양에 반영된다. 즉, \(\Delta_h\)를 \(\times\)1, \(\times\)2, \(\times\)3배 \(/dots\) 함에 따라 result image에서 반영되는 attribute또한 이에 맞게 변화한다는 것이다. 위의 그림에서 표현되어 있듯이 negative scaling에 대해서는 training을 하지 않았음에도 잘 적용 된다는 점을 알 수 있다.

Fig. 448 Linearity of h-space - Linear Combination#
서로 다른 attributes에 대한 \(\Delta_h\)를 합쳐서 부여를 했을 경우에도 각각의 attribute들이 image에 잘 반영이 된다는 점을 알 수 있다.
Robustness

Fig. 449 Robustness of h-space#
위의 그림은 h-space와 \(\epsilon-space\)에서 random noise를 주입했을 때의 결과를 비교한 것이다. h-space의 경우에는 random noise가 추가되었어도 image에 큰 변화가 없으며 많은 noise가 추가되었을 경우에도 image distortion은 거의 없고 semantic change만 발생한다. 그러나 \(\epsilon-space\)의 경우에는 random noise가 추가된 경우 image distortion이 심하게 발생한다. 이를 통해 h-space가 얼마나 robustness한지 알 수 있다.
Consistency across time steps

Fig. 450 Consistency across times steps of h-space#
h-space의 homogeneous한 성질을 통해 같은 attribute에 대한 \(\Delta h\)를 다른 image에 적용시켰을 때에도 잘 반영이 됌을 확인하였다. 저자들은 \(\Delta h_t\)들에 대한 평균인 \(\Delta h_t^{mean}\)을 적용시켰을 경우에도 result가 거의 비슷함을 보인다. Chapter4에서 제시한 Generative Process를 비추어 보았을 때, \(\Delta h_t\)는 Editing Process에서만 적용을 시킨다. 이 경우, 적용하는 \(\Delta h_t\)를 \(\Delta h_t^{global}\)이라고 칭하며, 적용하는 \(\Delta h_t\)가 interval동안 같은 크기 만큼 적용된다고 가정했을 경우, \(\Delta h^{global} = \cfrac{1}{\mathrm{T_e}}\sum_t\ \Delta h_t^{mean}\)이라고 쓸 수 있다. 이 경우에도 결과는 비슷함을 보여준다. 결국 원하는 attribute에 대해 주입해야 할 \(\Delta h\)양만 같다면, 원하는 editing 효과를 얻을 수 있다. 비록 이 논문에서는 best quality manipulation을 위해 \(\Delta h_t\)를 사용하였지만, \(\Delta h_t^{mean}\)과 \(\Delta h^{global}\)에 대해 더 연구를 해 볼 여지가 있다고 판단한다.
6. Conclusion#
본 논문에서는 Pretrained Diffusion models에서 latent semantic space인 h-space를 발견했고 h-space에서의 Asyrp(Asymmetric Reverse Process)와 새롭게 제안한 Reverse Process 방법을 통해 성공적인 image editing을 가능케 하였다. Diffusion model에서의 semantic한 latent space에 대한 첫 제안을 한 논문이다. h-space는 GAN의 latent space와 유사한 특성을 갖추고 있다. 대표적인 h-space의 특성으로는 Homogeneity, Linearity, Robustness, Consistency across timesteps이 있다.
