Information
Title: Latent Consistency Models: Synthesizing High-Resolution Images with Few-Step Inference
Reference
Project Page: https://latent-consistency-models.github.io/
Author: Donghyun Han
Last updated on May. 1, 2024
Latent Consistency Models#
1. Introduction#
Diffusion model은 다양한 분야에서 주목할만한 성과를 거두었지만 매우 느린 sampling 속도를 가지기 때문에 실시간 사용이 불가능하다. 이 같은 단점을 극복하기 위해 sampling 속도를 향상시키는 다양한 accelerating 방법이 제안되었다:
ODE solver의 성능개선을 통해 10~20 step만으로도 좋은 성능을 가지는 방법.
DPM-Solver (lu et al.)
사전 학습된 Diffusion model을 몇 step만으로도 추론할수 있도록 distillation하는 방법.
PD (Progressive Distillation). → 2 stage (Salimans et al.)
On Distillation of Guided Diffusion Models. (Meng et al.)
Consistency Models (Song et al.)
이중 특히 Consistency Models은 ODE-trajectory에 대한 일관성을 갖도록 하는 모델로서, single step만으로도 이미지를 생성할 수 있기 때문에 반복적인 계산이 필요하지 않다. 그러나 이 모델 또한 2가지의 단점을 가지고 있다:
Pixel space의 Flow-based Model이기 때문에 high-resolution 이미지 생성에 적합하지 않음.
Conditional(Classifer-free Guidance)한 이미지 생성을 고려하지 않아 text2img에 적합하지 않음.
본 논문의 제안점은 다음 3가지다:
빠르고 high-resolution 이미지를 생성하기 위한 Latent Consistency Models(LCMs)를 제안한다. LCMs은 영상의 latent space에 Consistency Models 개념을 적용해 매우 적은 step 만으로도 고품질의 이미지를 생성할 수 있다.
guided consistency distillation을 통해 Stable Diffusion을 매우 적은 step(1~4)으로 sampling 할 수 있는 방법을 제공한다. Skipping-Step이라는 테크닉을 통해 학습을 가속화 한다. 2, 4 step Model의 경우 학습에 A100 GPU 32시간 밖에 걸리지 않으며 LAION-5B-Aesthetics dataset에서 SOTA의 성능을 달성했다.
LCMs에 대한 새로운 fine-tuning 방식인 Latent Consistency Fine-tuning을 통해 빠른 추론 속도를 유지하면서도 Custom Dataset에 효율적으로 적용할 수 있다.

Fig. 507 768x768 Resolution image in 1~4 steps.#
2. Preliminaries#
Diffusion Models#
Diffusion Models 혹은 Score-based Models는 데이터에 점진적으로 Gaussian noise를 주입하고 reverse denoise process로 noise를 제거하여 데이터를 sampling하는 기법이다. 반면 forwad process는 원본 데이터 분포인 \(p_{data}(x)\)를 주변 확률분포인 \(q_{t}(x_{t})\)로 변환한다:
여기서 \(\alpha(t)\)와 \(\sigma(t)\)는 noise scheduler를 의미한다. 연속적인 timestep의 관점에서 이를 확률미분방정식(Stochastic Differential Equation, SDE)으로 나타낼 수 있는데, 다음과 같다:
또한 주변 확률분포 \(q_t(x)\)는 **Ptobability Flow ODE(PF-ODE)**라는 상미분방정식(Ordinary Differential Equation, ODE)을 만족하는데 다음과 같다:
이때 Diffusion model은 \(-\nabla\log{q_t(x_t)}\)(score function)를 예측하는 noise 예측 모델(\(\epsilon_\theta(x_t,t)\))을 학습시킨다. 학습된 모델은 score function의 근사치를 예측하고 sampling하는데 이를 empirical PF-ODE라 한다 (경험적 PF-ODE):
Classifier-Free Guidance (CFG)는 sampling의 퀄리티를 높이기 위해 GLIDE, Stable Diffusion, DALL\(\cdot\)E2, Imagen 등 다양한 conditional model에서 사용되었다. CFG의 scale \(\omega\)가 주어졌을 때 원본 noise prediction은 conditional, unconditional noise prediction을 선형적으로 혼합하여 대체된다:
Consistency Models#
Consistenct Model(CM)은 몇 step 혹은 한번의 step 만으로 데이터를 생성할 수 있는 모델이다. CM의 핵심은 PF-ODE의 궤적에 어떤 point와 PF-ODE의 solution에 대해 mapping되는 function (\(f:(x_t, t) \mapsto x_\epsilon\))을 추정하는 것이다.
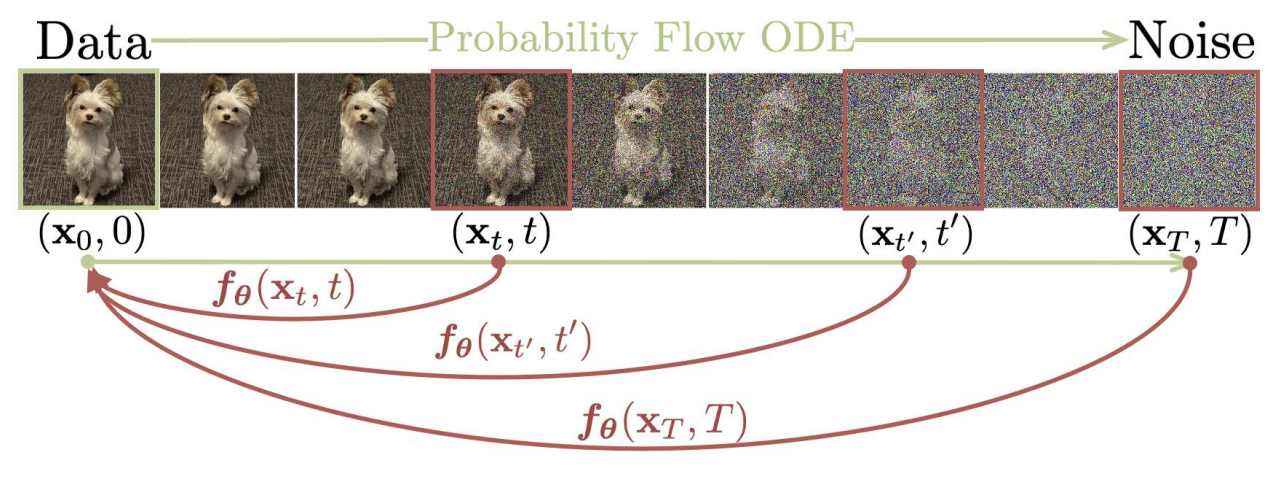
Fig. 508 Consistency Models (CM).#
\(\epsilon\)은 고정된 매우 작은 양수값을 가지며 CM의 function은 자기 자신에 대한 self-consistency를 만족해야한다. 즉 어떠한 time step에 대해서도 \(x_\epsilon\)을 sampling 할 수 있어야 한다.
\(f_\theta(x, \epsilon)=x\)를 만족하는 모델 \(f_\theta\)는 다음과 같이 정리할 수 있다:
\(c_{skip}(t)\)와 \(c_{out}(t)\)는 미분 가능한 함수이며 \(c_{skip}=1, c_{out}=0\)이기 때문에 \(f_\theta(x, \epsilon)=x\)를 만족한다. \(\theta\)는 학습 가능한 파라미터로 \(F_\theta\)는 심층 신경망을 의미한다.
CM은 pre-trained 모델에 대한 Distillation 방식과 scratch부터 학습하는 방식이 있는데 주로 Distillation 방식을 사용한다. Distillation 방식은 parameter \(\theta^-\)가 \(\theta\)를 통해 학습하며 모델에 대한 self-consistency를 위해 다음과 같이 손실함수를 구성한다:
이 때 \(\theta^-\)는 \(\theta\)에 대한 지수평균이동(Exponential Moving Average, EMA)이며 \(\theta^- \leftarrow \mu\theta^-+(1-\mu)\theta\)이다. \(d(\cdot, \cdot)\)은 두 sample 사이의 거리를 측정하는 지표이다. \(\hat{x}^{\phi}_{t_n}\)은 \(x_{t_{n+1}}\)에 대한 \(x_{t_n}\)을 추정한 값으로 다음과 같다:
\(\Phi\)는 PF-ODE에 사용되는 ODE Solver로 Euler나 Heun Method등의 수치적인 ODE solver를 사용할 수 있다. 즉 Consistency Distillation은 ODE Solver로 예측한 \(\hat{x}^{\phi}_{t_n}\)과 \(x_{t_{n+1}}\)을 입력으로 \(f_{\theta^-}\)와 \(f_\theta\)로 예측한 값의 Consistency를 비교하는 방식으로 Distillation을 수행한다.
3. Latent Consistency Models#
CM의 한계:
ImageNet 64x64, LSUN 256x256 영상에 대한 Generation만 수행
High Resolution의 잠재성이 아직 탐구되지 않았음.
Classifier-free Guidance(CFG) 등을 사용하지 않음.
Latent Consistency Models(LCMs)는 CM의 잠재력을 충분히 발휘하여 좀더 도전적인 task를 수행한다.
3.1 Consistency Distillation in the Latent Space#
본 논문에서는 pre-trained 된 Stable Diffusion에 Consistency Distillation을 적용한 Latent Consistency Distillation (LCD)을 제안한다. LCMs는 LDM(SD)을 기반으로 설계되었기 때문에 \(z=\varepsilon(x)\)를 통해 \(x\)를 latent vector로 임베딩하고 \(\hat{x}=\mathcal{D}(z)\)를 통해 원본 영상으로 복원한다. latent space 상에서 연산이 이뤄지기 때문에 Computation Cost를 크게 줄일 수 있어 high-resolution 영상을 laptop GPU에서 생성할 수도 있다.
condition을 추가한 PF-ODE의 reverse process는 다음과 같이 정의된다:
\(z_t\)는 t step의 image latents, \(\epsilon_\theta(z_t,c,t)\)는 noise 예측 모델, c는 text와 같은 conditional prompt를 의미한다. PF-ODE상에서 모든 t step에 대해 consistency function \(f_\theta :(z_t,c,t) \mapsto z_0\)이기 때문에 이를 수식으로 정리하자면 다음과 같이 나타낼 수 있다 (\(\hat{\epsilon}_\theta\)는 noise prediction model.):
수식을 살펴보면 ddpm 등의 reparameterization trick인 \(x_t := \sqrt{\bar{\alpha}_t}x_0 + \sqrt{1-\bar{\alpha}_t}\epsilon\)을 변형하여 식에 대입한 것을 알 수 있음. (\(x\)→\(z\)로 치환)
CM과 마찬가지로 \(c_{skip}(0)=1, c_{out}(0)=0\)이고 \(\hat{\epsilon}_{\theta}(z,c,t)\)는 teacher diffusion model과 유사한 noise 예측 모델 parameter이다. \(f_\theta\)는 \(\epsilon-Prediction\) 외에도 \(x-Prediction\)이나 \(v-Prediction\)을 사용할 수도 있다. (\(x-Prediction\)은 DDPM, \(v-prediction\)은 PD에서 나온 개념)
\(\psi(z_t,t,x,c)\)는 ODE solver이며 특정한 time step \(t \sim s\) 사이에 대한 Eq. 8의 우항을 근사한 값이다. ODE Solver이기 때문에 DDIM, DPM-Solver, DPM-Solver++ 등을 사용할 수 있다. 또한 \(\psi\)는 학습 및 Distillation시에만 사용한다. 이때 \(t_n\)은 EDM을 토대로 CM에서 나오는 값이다. 기존 timestep \([t, T]\)에 대한 하위 간격으로 \(t_1=\epsilon<t_2<\cdots<t_N=T\)인 어떠한간격을 의미한다. \(t_i\)는 다음과 같이 나타낼 수 있다:
Eq, 8을 \(t_{n+1} \sim t_n\)까지 t에 대해 적분 했을 때 다음과 같은 수식을 얻을 수 있다:
3.2 One-Stage Guided Distillation by solving augmented PF-ODE#
Clasifier-free Guidance(CFG)는 high-quality의 conditional 이미지 생성을 가능하게 했다. 다만 CFG는 2개의 Diffusion Model을 훈련해야하기 때문에 효율적이지 못하며, LCMs와 같은 few-step sampling method에 사용하기 힘들다. 따라서 이를 해결하기 위해 본 논문에서는 CFG를 Distillation 과정에서 통합하였다.
Guided-Distill의 경우 two-stage Distillation을 통해 few-step sampling에 CFG를 통합하였으나 학습시간이 길고 2단계를 거치며 손실이 누적되기 때문에 최적의 성능을 내기 힘들다.
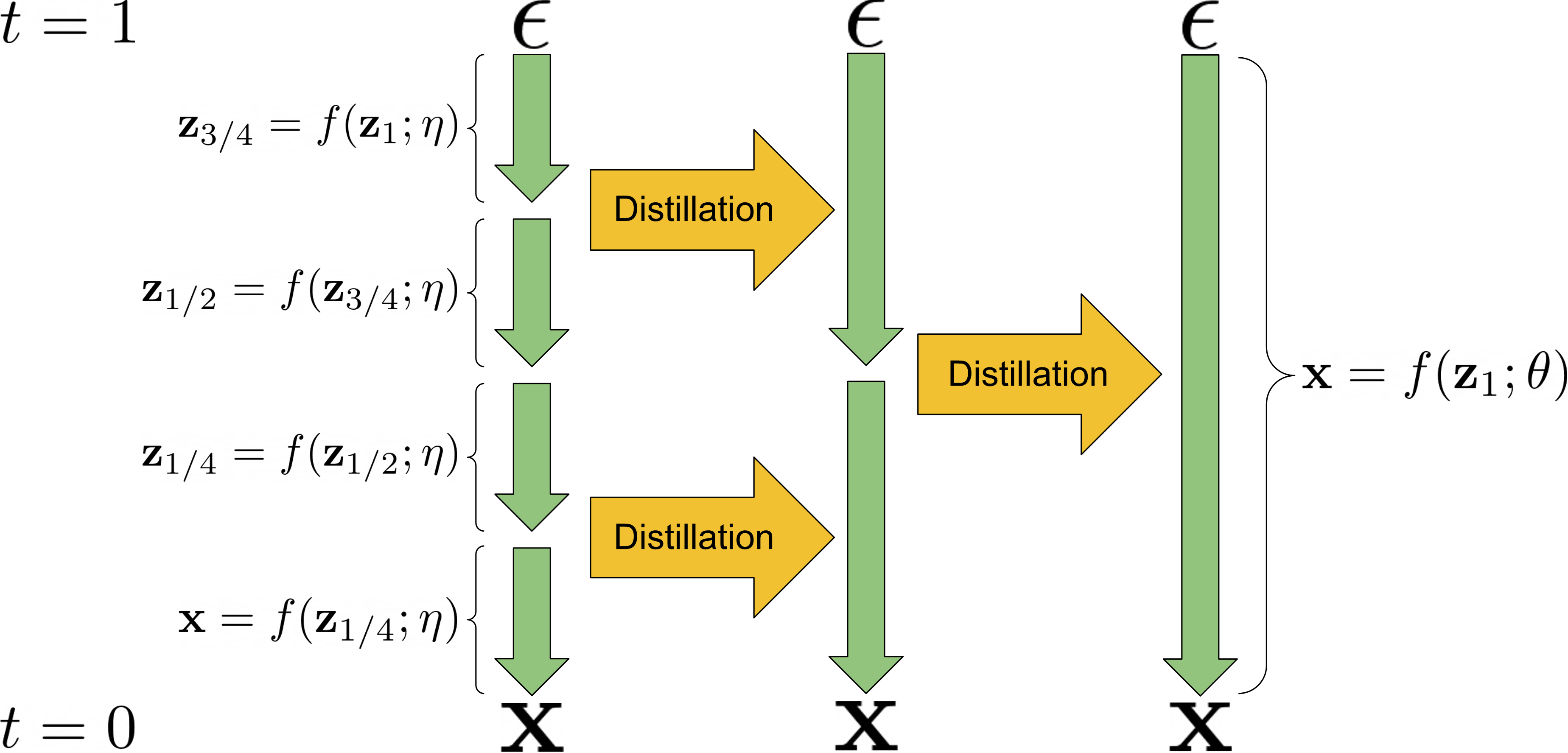
Fig. 509 2 Stage Distillation.#
t이에 반해 LCMs는 augmented PF-ODE를 해결하는 방식으로 one-stage의 guided Distillation을 제안했다. 일단 CFG에 대한 reverse diffusion process는 다음과 같다:
CFG는 conditional noise 예측값과 unconditional noise 예측값을 선형 결합하여 사용한다. 즉 noise 값이 \(\omega\)에 따라 변형되므로 augmented PF-ODE라고 한다. augmented PF-ODE는 다음과 같이 나타낼 수 있다:
consistency function도 \(\omega\)를 변수로 받아오기 때문에 \(f_\theta:(z_t,\omega,c,t)\mapsto z_0\)로 다시 정의된다. Consistency Distillation Loss 또한 다음과 같이 나타낼 수 있다:
\(\omega\)와 \(n\)는 각각 \([\omega_{min}, \omega_{max}]\), \(\{1,…,N-1\}\)에서 sampling된다. \(\hat{z}^{\psi, \omega}_{t_n}\)는 이전과 마찬가지로 CFG가 추가된 ODE-Solver를 사용하여 근사한 값을 의미한다. 이때 사용되는 새로운 noise 예측모델 \(\tilde{\epsilon}_\theta(z_t,\omega,c,t)\)는 Eq. 11처럼 \(t_{n+1} \sim t_n\)까지 t에 대해 적분 했을 때 다음과 같이 나타낼 수 있다:
마찬가지로 PF-ODE Solver \(\psi(\cdot,\cdot,\cdot,\cdot)\)에는 DDIM, DPM-Solver, DPM-Solver++ 등을 사용할 수 있다.
3.3 Accelerating Distillation with Skipping Time Steps#
Stable Diffusion 등 보통의 Diffusion Model들은 매우 큰 step을 전체 time step으로 잡고 학습한다. 그러나 이같이 촘촘한 time step은 각 \(t_n\)과 \(t_{n+1}\)의 변화량을 감소시키기 때문에 자연스럽게 Consistency Distillation Loss도 작아지게 된다. Loss가 작아지면 학습의 수렴속도도 느려지게 된다. 따라서 LCMs는 학습 수렴의 속도를 높이기 위해 time step을 수천에서 수십으로 크기 단축시키는 SKIPPING-STEP 방법을 제안하였다.
기존 CMs 모델의 경우 time scheduler로 EDM을 사용하고 ODE-Solver로 Euler 방법이나 Heun 방법을 사용한다. 그러나 LCMs는 Eq. 8을 통해 DDIM, DPM-Solver, DPM-Solver++와 같은 효율적인 solver도 효과적으로 데이터를 생성할 수 있다는 것을 증명했다. 따라서 SKIPPING-STEP 방법은 \(t_{n+1} → t_n\) 사이의 Consistency를 비교하는것이 아니라 특정 k-step만큼 거리가 있는 time step에 대한 Consistency를 비교한다. (\(t_{n+k}→t_n\))
이때 \(k\)값의 크기는 trade-off 관계를 가진다. 너무작으면 (\(k=1\)) 기존과 같이 느린 수렴속도를 갖게되며, 너무 큰 값일 때는 ODE solver 를 통해 근사할 때 오차가 매우 커질수 있다. 논문의 저자는 \(k=20\)을 사용해 time step을 수천에서 수십으로 대폭 줄여 학습을 Accelerating 할 수 있었다. Eq. 14에 k값을 추가해 SKIPPING-STEP을 표현할 수 있다.
\(\hat{z}^{\psi, \omega}_{t_n}\)에 대한 수식도 다음과 같이 변경할 수 있다.
3.4 Latent Consistency Fine-tuning for customized dataset#
Stable Diffusion과 같은 Foundation 생성 모델은 거의 대부분의 text-to-image Generation task에서 잘 되지만 가끔 downstream task를 위해 Cunstom dataset에 대한 fine-tuning이 필요할 때가 있다. Latent Consistency Fine-tuning(LCF)는 Custom Dataset도 teacher model에 대한 종속없이 few-step inference를 성공적으로 할수 있도록 한다. 따라서 LCM은 기존의 Diffusion model에 대한 추가적인 fine tuning 방법론 없이도 Custom Dataset을 바로바로 학습하여 사용할수 있다.
따로 추가적인 fine-tuning 방법이 있는것은 아니고 Consisteny Distillation 시 pre-trained 된 LDM을 사용하여 EMA를 통해 Distillation을 하기 때문에 Dataset을 Custom Dataset으로 사용하기만하면 된다. 즉 pre-trained Diffuson model → Custom Dataset fine-tuning → few step inference를 위한 Consistency Distillation을 할 필요 없이 바로학습이 가능하다는 의미이다.
4. Experiments#
4.1 Text-To-Image Generation#
3가지 데이터셋에 대한 평가를 진행했다. (LAION-5B, LAION-Aesthetics-6+(12M), LAION-Aesthetics-6.5+(650k)) 앞서말한것처럼 하나의 Resolution이 아닌 512x512, 768x768의 high resolution을 생성했다. 512 size는 \(\epsilon\)-prediction, 768 size는 \(v\)-prediction을 사용했고 ODE-Solver로는 DDIM을 사용했다. 앞서말한것처럼 SKIPPING-STEP은 20의 값을 가진다.
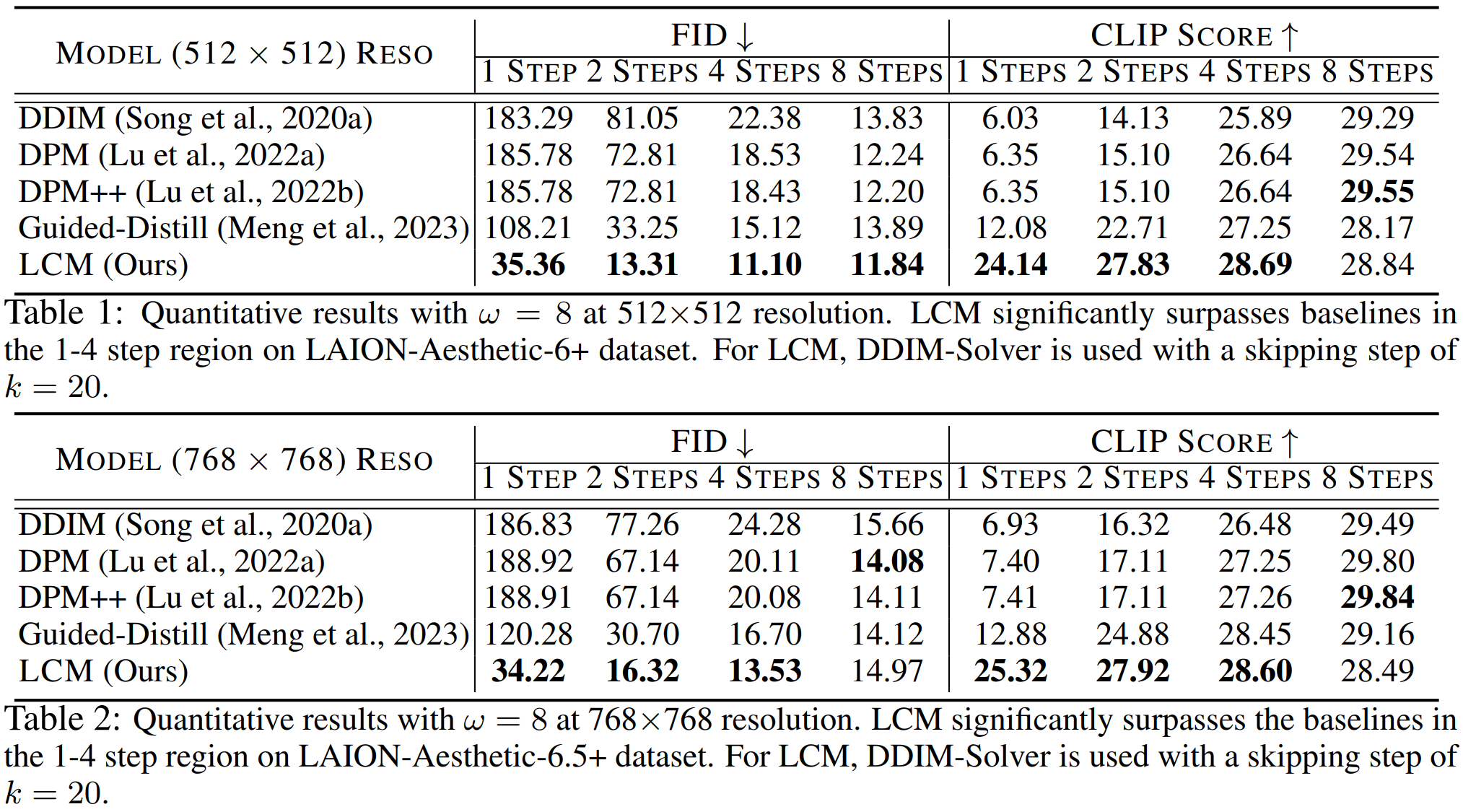
Fig. 510 Quantitative results at 512 x 512 & 768 x 768 resolution.#

Fig. 511 Qualitative results on LAION-Aesthetic-6.5+ Dataset. (2,4 steps)#
DDIM, DPM-Solver, DPM-Solver++, Guided-Distill 4가지 모델에 대해 LCM과 성능비교를 했는데 이때 Guided-Distill은 오픈소스 코드가 없기 때문에 논문의 내용과 동일하게 Implementation 해서 성능을 비교하였다. LCM은 같은 메모리 Cost 대비 더 빠르게 수렴하고 더 좋은 품질의 영상을 생성하였다. 특히 Guided-Distill은 2 stage Distillation이지만 LCM은 1 Stage만 사용해도 이같은 성능을 보여줬다.
4.2 Abulation Study#
ODE Solvers & Skipping-Step Schedule#
augmented PF-ODE를 푸는 solver들(DDIM, DPM, DPM++)을 LCM에 사용할 때 성능 비교와 SKIPPING-STEP schedule의 \(k\)값에 따른 성능 변화를 비교하였다. 모든 모델은 2,000 iteration에서의 4-step inference로 고정해서 비교했다.
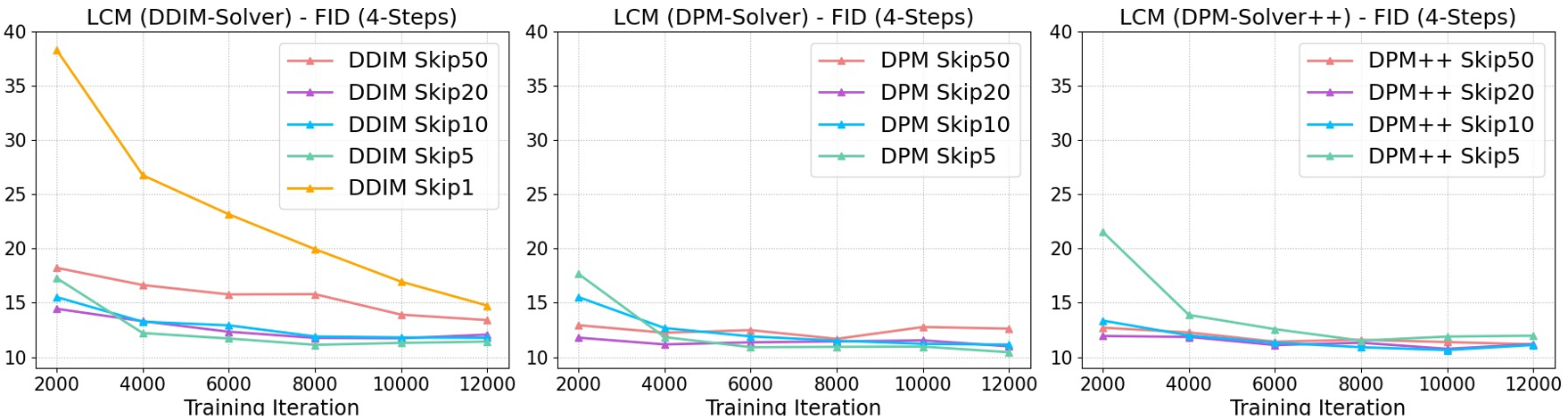
Fig. 512 Different ODE solvers and skipping step k.#
Skipping step의 경우 \(k\) 값을 올렸을 때 훨씬더 빠르게 수렴하며 때때로 더 좋은 FID 값을 보여주었다. 또한 DPM과 DPM++은 \(k\)가 50일 때 DDIM보다 더 좋은 성능을 보였다. 이는 \(k\) 값이 클수록 더 큰 ODE approximation error를 가지는 DDIM에 비해 오차가 적기 때문이다.
\(k=20\)일 때, 3가지 모델 모두 좋은 성능이 보였다.
The Effect of Guidance Scale \(\omega\)#
일반적으로 \(\omega\)값이 클수록 CLIP score 같은 품질의 지표는 좋아지지만 작을수록 다양성이 떨어져 FID Score가 떨어진다. 즉 \(\omega\)의 크기는 Quality와 Diversity에 대한 trade-off가 있다.
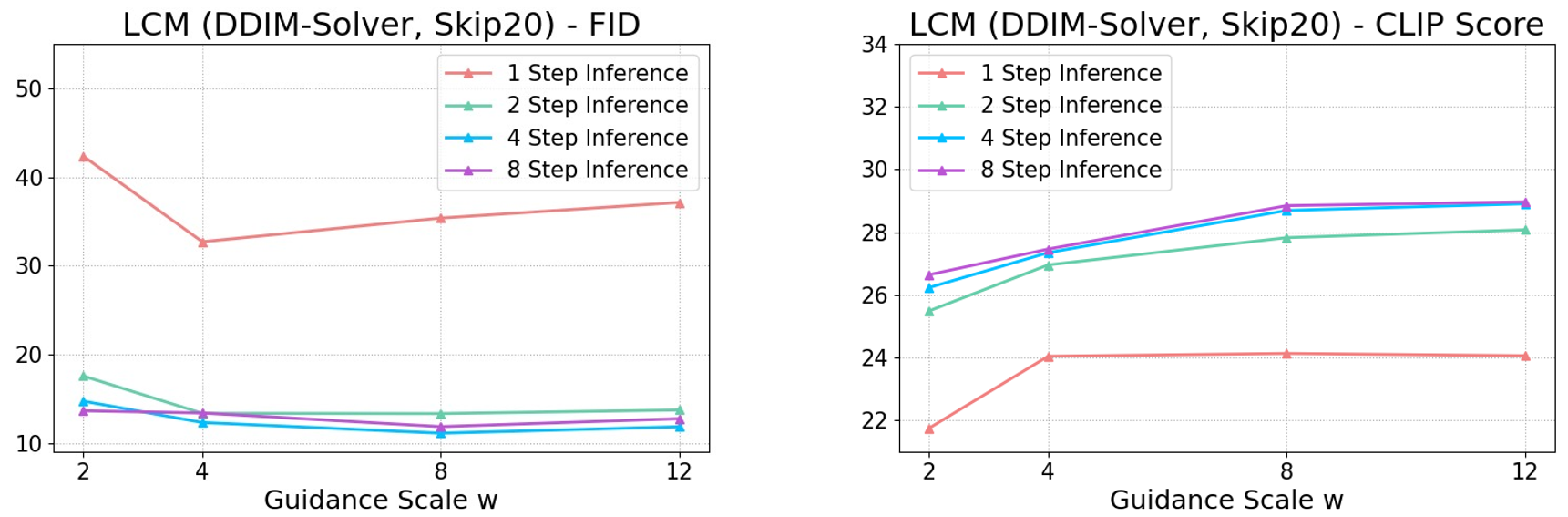
Fig. 513 Different classifier-free guidance scales \(\omega\).#
그래프를 보면 2~8 step inference는 성능에 큰 차이를 가지지는 않는것으로 확인된다. 그러나 1 step inference는 아직 개선의 여지가 있는것을 확인할 수 있다.

Fig. 514 Different classifier-free guidance scales \(\omega\).#
\(\omega\)에 따른 실제 생성 이미지를 비교해 봤을 때 생성 영상의 Quality 차이가 확연하게 들어난다. 즉 Distillation 시에도 CFG를 적용하는 것이 성능을 크게 개선할 수 있다는 것을 증명한다.
4.3 Downstream Consistency Fine-tuning Results#
포켓몬 데이터셋과 심슨 데이터셋에 LCF를 적용했을 때를 비교하였다. 90%는 학습 데이터로, 10%는 검증 데이터로 사용했다. 완벽하진 않지만 Custom Dataset의 style을 잘 catch한 모습을 보여준다.

Fig. 515 Latent Consistency Fine-tuning(LCF) on two customized dataset.. \(\omega\).#
Conclusion#
LCM은 Consistency Distillation을 Latent 상에 적용하여 고화질의 영상을 매우 적은 time step으로 inference 할 수 있도록 한 모델이다. 즉 성능 좋고 고해상도의 영상을 few-step으로 가능하게 만들었다. 특히 Custom Dataset에도 Distillation을 적용했을 때 적은 time step으로도 어느정도의 style을 간단하게 학습하는 결과를 보여주었다.
