Information
Title: Denoising Diffusion Probabilistic Models (NeurIPS 2020)
Reference
Author: Beomsoo Park
Last updated on Apr. 19, 2023
DDPM#

Fig. 13 DDPM samples \ (source: https://arxiv.org/abs/2006.11239)#
1. Introduction#
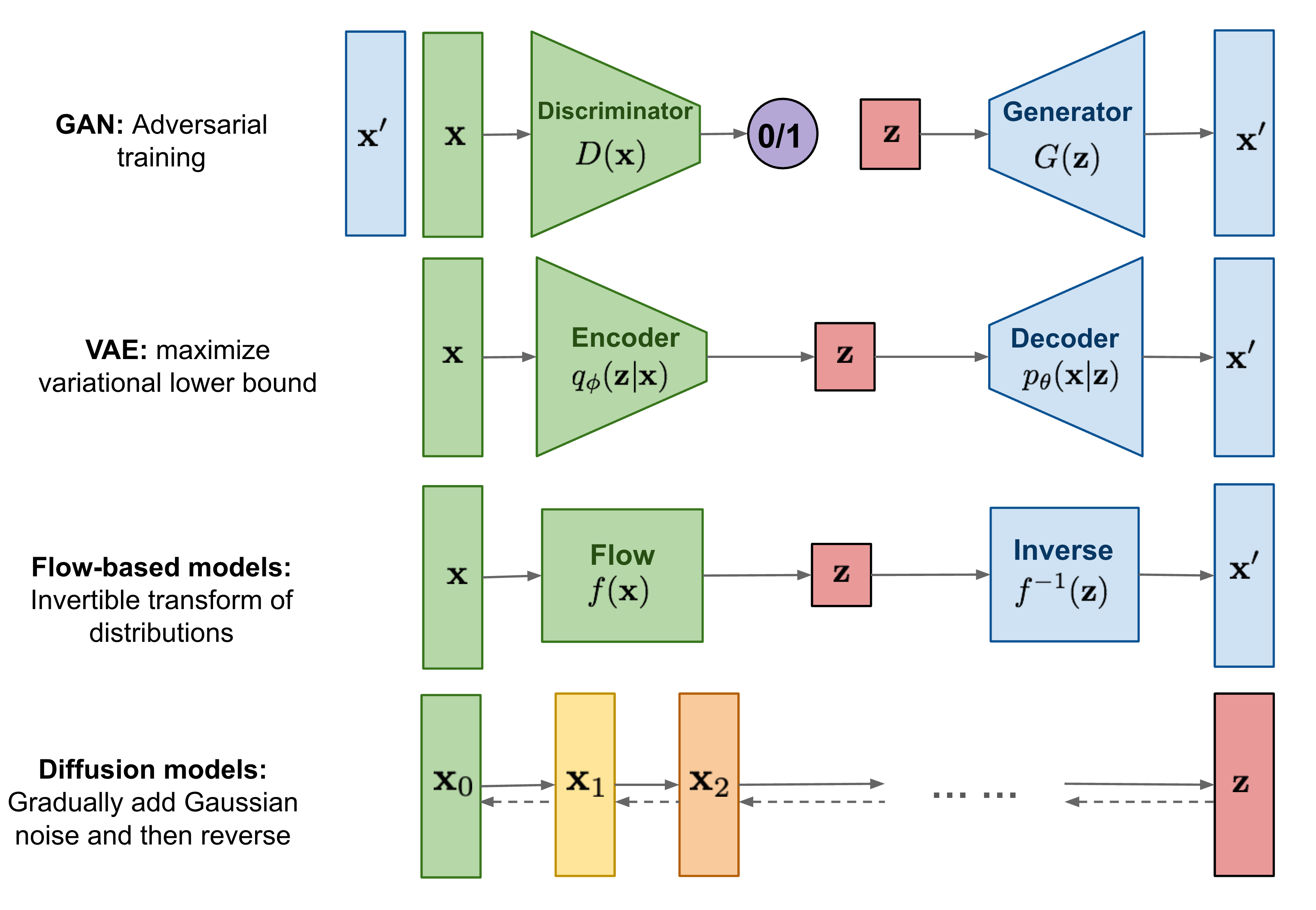
Fig. 14 Diffusion models \ (source: https://velog.io/@yetsyl0705/What-are-Diffusion-Models)#
Diffusion model은 variational inference로 학습시켜 데이터를 생성하는 parameterized Markov chain. Diffusion model은 Markov가 데이터가 normal distribution의 형태를 할 때까지 noise를 더해가는 diffusion process와 이를 역으로 거치며 학습하는 reverse process로 구성됨.
Diffusion model은 정의하기 쉽고 학습시키는 것도 편리함. 또한 높은 품질의 sample(output)도 생성이 가능.
Variational inference(변분추론): 사후확률(posterior) 분포 \(p(z |x)\)를 다루기 쉬운 확률분포 \(q(z)\)로 근사(approximation)하는 것
Parameterize: 하나의 표현식에 대해 다른 parameter를 사용하여 다시 표현하는 과정. 이 과정에서 보통 parameter의 개수를 표현 식의 차수보다 적은 수로 선택(ex. 3차 표현식 –> 2개 parameter 사용)하므로, 낮은 차수로의 mapping 함수(ex. 3D –> 2D)가 생성
Markov chain: 어떤 상태에서 다른 상태로 넘어갈 때, 바로 전 단계의 상태에만 영향을 받는 확률 과정
2. Background#
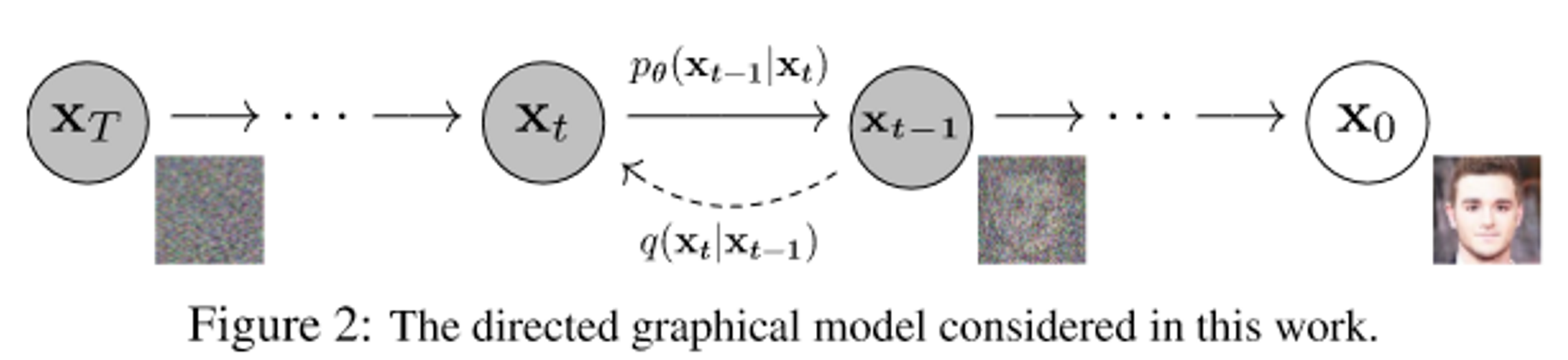
Fig. 15 Graphical model of DDPM \ (source: https://arxiv.org/abs/2006.11239)#
2-1. Forward(diffusion) process \(q(\mathbf{x}_t|\mathbf{x}_{t-1})\)#
Markov chain으로 data에 noise를 추가하는 과정. Noise를 추가할 때 variance schedule \(\beta_1,,,\beta_T\)로 scaling을 한 후 더해준다.
\(\beta_t = 1\)이면 mean인 \(\sqrt{1-\beta_t}\mathbf{x}_{t-1} = 0\). 이전 정보를 갖지 못하고 노이즈가 증가함
단순히 noise만을 더해주는게 아니라 \(\sqrt{1-\beta_t}\)로 scaling하는 이유는 variance가 발산하는 것을 막기 위함
\(q(x_1|x_0)\): \(x_0\)에 noise를 추가해 \(x_1\)을 만드는 과정
\(x_T\)는 완전 destroy된 noise 상태 ~ \(N(x_T;0, I)\)
2-2. Reverse process \(p(\mathbf{x}_{t-1}|\mathbf{x}_t)\)#
Reverse process로 가우시안 노이즈를 사용하는 이유는 1994년 논문에 forward process가 가우시안이면 reverse process도 가우시안으로 쓰면 된다라는 증명이 있다고 함.
여기서 우리가 해야 할 것은 \(\mathbf{x}_t\)를 보고 \(\mathbf{x}_{t-1}\)의 평균 \(\mu_\theta\)과 분산 \(\Sigma_\theta\)을 예측해내는 것.
Hierarachical VAE에서의 decoding 과정과 비슷함
\(\mu_\theta\)과 분산 \(\Sigma_\theta\)는 학습 가능한 parameter
2-3. Loss Function \(L\)#
Diffusion model의 목적은 **noise를 어떻게 제거할 것인가?**이다. \(x_t\)가 들어왔을 때 \(x_{t-1}\)을 예측할 수 있다면 \(x_0\) 또한 예측이 가능해짐.
본 논문에서는 negative log likelihood를 최소화하는 방향으로 진행. 위 수식을 ELBO(Evidence of Lower BOund)로 우항과 같이 정리하고 이를 풀어내면
ELBO의 역할은 우리가 관찰한 P(z|x)가 다루기 힘든 분포를 이루고 있을 때 이를 조금 더 다루기 쉬운 분포인 Q(x)로 대신 표현하려 하는 과정에서 두 분포 (P(z|x)와 Q(x))의 차이 (KL Divergence)를 최소화 하기 위해 사용된다.
와 같은 결과가 나온다.
\(L_T\): Regularization term으로 \(\beta_t\)를 학습시킴
\(L_{t-1}\): Reconstruction term으로 매 단계에서 noise를 지우는 지움
\(L_0\): Reconstruction term으로 최종 단계에서 image를 생성
3. Diffusion models and denoising encoders#
DDPM에서는 inductive bias를 늘려 모델을 더 stable하고 성능도 개선할 수 있었음.
Inductive bias: 학습 모델이 지금까지 만나보지 못했던 상황에서 정확한 예측을 하기 위해 사용하는 추가적인 가정, 즉 우리가 풀려는 문제에 대한 정보를 모델에 적용하는 것
3-1. Forward process and \(L_T\)#
\(\beta_t\)를 고정했더니 학습이 잘됨. 10^-4 ~ 0.02로 linear하게 image에 가까울수록 noise를 적게 주는 방식으로 설정.
따라서 \(q\)에는 학습 가능한 parameter가 없어 \(L_T\)는 0이 되기 때문에 삭제할 수 있었음.
3-2. Reverse process and \(L_{1:T-1}\)#
\( q\left(x_{t-1} \mid x_t, x_0\right)=N\left(x_{t-1} ; \tilde{\mu}\left(x_t, x_0\right), \tilde{\beta}_t \mathrm{I}\right) \)
\( p_\theta\left(x_{t-1} \mid x_t\right)=\mathcal{N}\left(x_{t-1} ; \mu_\theta\left(x_t, t\right), \sum_\theta\left(x_t, t\right)\right) \)
\(L_{1:T-1}\)는 forward progress posterior를 예측하는 loss. \(\mathbf{x}_{t-1}\)에서 noise를 더해 \(\mathbf{x}_{t}\)를 만들었을때, 그 과정을 복원 \(p(\mathbf{x}_{t-1}|\mathbf{x}_t)\) 하는 과정을 학습.

Fig. 16 Loss Simplication \ (source: https://velog.io/@sjina0722/논문-리뷰-Denoising-Diffusion-Probabilistic-Models)#
\(\Sigma_\theta\): \(\beta\)를 상수로 가정했고 \(p(\mathbf{x}_{t-1}|\mathbf{x}_t)\)의 variance가 \(\beta\)에 영향을 받기 때문에 학습시키지 않아도 된다고 생각해 variance term을 제거함.
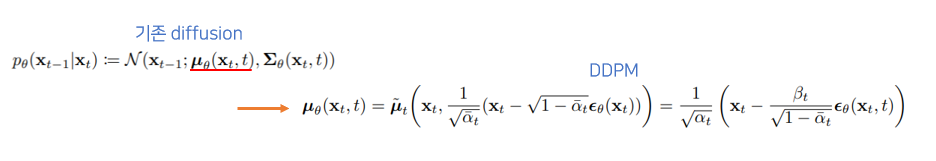
Fig. 17 Residual Estimation \ (source: https://velog.io/@sjina0722/논문-리뷰-Denoising-Diffusion-Probabilistic-Models)#
\(\mu_\theta\): DDPM에서는 \(\mu_\theta\)를 바로 구하지 않고 residual \(\epsilon_\theta\)만 구해 정확도를 높임.
3-3. Data scaling, reverse process decoder and \(L_0\)#
[0, 255]의 image를 [-1,1] 사이로 linearly mapping. Sampling 마지막 단계에는 noise를 추가하지 않음.
\(L_0\)은 두 normal distribution 사이의 KL divergence를 나타냄.
\(D\): Data dimensionality
\(i\): 좌표
3-4. Simplified training objective#

Fig. 18 Simplified training objective \ (source: https://velog.io/@sjina0722/논문-리뷰-Denoising-Diffusion-Probabilistic-Models)#
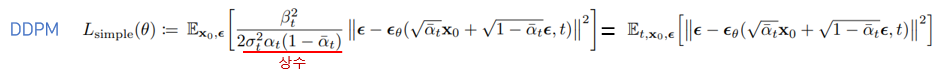
Fig. 19 Final Loss \ (source: https://velog.io/@sjina0722/논문-리뷰-Denoising-Diffusion-Probabilistic-Models)#
최종 loss는 위와 같이 나타난다. Ground truth - estimated output간 MSE loss를 줄이는 과정이 denoising과 비슷해 DDPM이라는 이름이 붙음.
Simplified objective을 통해 diffusion process를 학습하면 매우 작은 t 에서뿐만 아니라 큰 t에 대해서도 network 학습이 가능하기 때문에 매우 효과적.

Fig. 20 Psuedo code of training process \ (source: https://arxiv.org/abs/2006.11239)#
Algorithm 1: Training
Noise를 더해나가는 과정, network(\(\epsilon_\theta\), \(p_\theta\))가 t step에서 noise(\(\epsilon\))가 얼마만큼 더해졌는지를 학습한다.
학습 시에는 특정 step의 이미지가 얼마나 gaussian noise가 추가되었는지를 예측하도록 학습된다.
코드에서는 랜덤 노이즈와 시간 단계 t로 노이즈가 추가된 이미지를 얻고 해당 이미지를 보고 모델이 노이즈를 예측
def p_losses(self, x_start, t, noise = None):
b, c, h, w = x_start.shape
noise = default(noise, lambda: torch.randn_like(x_start))
# noise sample
x = self.q_sample(x_start = x_start, t = t, noise = noise)
# if doing self-conditioning, 50% of the time, predict x_start from current set of times
# and condition with unet with that
# this technique will slow down training by 25%, but seems to lower FID significantly
x_self_cond = None
if self.self_condition and random() < 0.5:
with torch.no_grad():
x_self_cond = self.model_predictions(x, t).pred_x_start
x_self_cond.detach_()
# predict and take gradient step
model_out = self.model(x, t, x_self_cond)
if self.objective == 'pred_noise':
target = noise
elif self.objective == 'pred_x0':
target = x_start
elif self.objective == 'pred_v':
v = self.predict_v(x_start, t, noise)
target = v
else:
raise ValueError(f'unknown objective {self.objective}')
loss = self.loss_fn(model_out, target, reduction = 'none')
loss = reduce(loss, 'b ... -> b (...)', 'mean')
loss = loss * extract(self.loss_weight, t, loss.shape)
return loss.mean()
Algorithm 2: Sampling
Network를 학습하고 나면, gaussian noise에서 시작해서 순차적으로 denoising 하는 것이 가능하다. (by parameterized markovian chain)
코드에서는 noise 제거 후 소량의 noise를 다시 추가하고 있음
@torch.no_grad()
def p_sample(self, x, t: int, x_self_cond = None):
b, *_, device = *x.shape, x.device
batched_times = torch.full((b,), t, device = x.device, dtype = torch.long)
model_mean, _, model_log_variance, x_start = self.p_mean_variance(x = x, t = batched_times, x_self_cond = x_self_cond, clip_denoised = True)
noise = torch.randn_like(x) if t > 0 else 0. # no noise if t == 0
pred_img = model_mean + (0.5 * model_log_variance).exp() * noise
return pred_img, x_start
4. Experiments#
T: 1000
backbone: U-Net
각 down/upsampling 단계는 ResNet/ConvNext 블록 2개 + (groupnorm + attention + residual) + down/upsampling으로 구성됨
block_klass = partial(ResnetBlock, groups = resnet_block_groups)
self.downs.append(nn.ModuleList([
block_klass(dim_in, dim_in, time_emb_dim = time_dim),
block_klass(dim_in, dim_in, time_emb_dim = time_dim),
Residual(PreNorm(dim_in, LinearAttention(dim_in))),
Downsample(dim_in, dim_out) if not is_last else nn.Conv2d(dim_in, dim_out, 3, padding = 1)
]))
self.ups.append(nn.ModuleList([
block_klass(dim_out + dim_in, dim_out, time_emb_dim = time_dim),
block_klass(dim_out + dim_in, dim_out, time_emb_dim = time_dim),
Residual(PreNorm(dim_out, LinearAttention(dim_out))),
Upsample(dim_out, dim_in) if not is_last else nn.Conv2d(dim_out, dim_in, 3, padding = 1)
]))
class Unet(nn.Module):
def __init__(
self,
dim,
init_dim = None,
out_dim = None,
dim_mults=(1, 2, 4, 8),
channels = 3,
self_condition = False,
resnet_block_groups = 8,
learned_variance = False,
learned_sinusoidal_cond = False,
random_fourier_features = False,
learned_sinusoidal_dim = 16
):
super().__init__()
# determine dimensions
self.channels = channels
self.self_condition = self_condition
input_channels = channels * (2 if self_condition else 1)
init_dim = default(init_dim, dim)
self.init_conv = nn.Conv2d(input_channels, init_dim, 7, padding = 3)
dims = [init_dim, *map(lambda m: dim * m, dim_mults)]
in_out = list(zip(dims[:-1], dims[1:]))
block_klass = partial(ResnetBlock, groups = resnet_block_groups)
# time embeddings
time_dim = dim * 4
self.random_or_learned_sinusoidal_cond = learned_sinusoidal_cond or random_fourier_features
if self.random_or_learned_sinusoidal_cond:
sinu_pos_emb = RandomOrLearnedSinusoidalPosEmb(learned_sinusoidal_dim, random_fourier_features)
fourier_dim = learned_sinusoidal_dim + 1
else:
sinu_pos_emb = SinusoidalPosEmb(dim)
fourier_dim = dim
self.time_mlp = nn.Sequential(
sinu_pos_emb,
nn.Linear(fourier_dim, time_dim),
nn.GELU(),
nn.Linear(time_dim, time_dim)
)
# layers
self.downs = nn.ModuleList([])
self.ups = nn.ModuleList([])
num_resolutions = len(in_out)
for ind, (dim_in, dim_out) in enumerate(in_out):
is_last = ind >= (num_resolutions - 1)
self.downs.append(nn.ModuleList([
block_klass(dim_in, dim_in, time_emb_dim = time_dim),
block_klass(dim_in, dim_in, time_emb_dim = time_dim),
Residual(PreNorm(dim_in, LinearAttention(dim_in))),
Downsample(dim_in, dim_out) if not is_last else nn.Conv2d(dim_in, dim_out, 3, padding = 1)
]))
mid_dim = dims[-1]
self.mid_block1 = block_klass(mid_dim, mid_dim, time_emb_dim = time_dim)
self.mid_attn = Residual(PreNorm(mid_dim, Attention(mid_dim)))
self.mid_block2 = block_klass(mid_dim, mid_dim, time_emb_dim = time_dim)
for ind, (dim_in, dim_out) in enumerate(reversed(in_out)):
is_last = ind == (len(in_out) - 1)
self.ups.append(nn.ModuleList([
block_klass(dim_out + dim_in, dim_out, time_emb_dim = time_dim),
block_klass(dim_out + dim_in, dim_out, time_emb_dim = time_dim),
Residual(PreNorm(dim_out, LinearAttention(dim_out))),
Upsample(dim_out, dim_in) if not is_last else nn.Conv2d(dim_out, dim_in, 3, padding = 1)
]))
default_out_dim = channels * (1 if not learned_variance else 2)
self.out_dim = default(out_dim, default_out_dim)
self.final_res_block = block_klass(dim * 2, dim, time_emb_dim = time_dim)
self.final_conv = nn.Conv2d(dim, self.out_dim, 1)
def forward(self, x, time, x_self_cond = None):
if self.self_condition:
x_self_cond = default(x_self_cond, lambda: torch.zeros_like(x))
x = torch.cat((x_self_cond, x), dim = 1)
x = self.init_conv(x)
r = x.clone()
t = self.time_mlp(time)
h = []
for block1, block2, attn, downsample in self.downs:
x = block1(x, t)
h.append(x)
x = block2(x, t)
x = attn(x)
h.append(x)
x = downsample(x)
x = self.mid_block1(x, t)
x = self.mid_attn(x)
x = self.mid_block2(x, t)
for block1, block2, attn, upsample in self.ups:
x = torch.cat((x, h.pop()), dim = 1)
x = block1(x, t)
x = torch.cat((x, h.pop()), dim = 1)
x = block2(x, t)
x = attn(x)
x = upsample(x)
x = torch.cat((x, r), dim = 1)
x = self.final_res_block(x, t)
return self.final_conv(x)
16 x 16 feature map resolution에 self-attention. conv에서 차원을 3배로 늘리고 q,k,v로 분해.
class Attention(nn.Module):
def __init__(self, dim, heads = 4, dim_head = 32):
super().__init__()
self.scale = dim_head ** -0.5
self.heads = heads
hidden_dim = dim_head * heads
self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias = False)
self.to_out = nn.Conv2d(hidden_dim, dim, 1)
def forward(self, x):
b, c, h, w = x.shape
qkv = self.to_qkv(x).chunk(3, dim = 1)
q, k, v = map(lambda t: rearrange(t, 'b (h c) x y -> b h c (x y)', h = self.heads), qkv)
q = q * self.scale
sim = einsum('b h d i, b h d j -> b h i j', q, k)
attn = sim.softmax(dim = -1)
out = einsum('b h i j, b h d j -> b h i d', attn, v)
out = rearrange(out, 'b h (x y) d -> b (h d) x y', x = h, y = w)
return self.to_out(out)
Linear attention
class LinearAttention(nn.Module):
def __init__(self, dim, heads = 4, dim_head = 32):
super().__init__()
self.scale = dim_head ** -0.5
self.heads = heads
hidden_dim = dim_head * heads
self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias = False)
self.to_out = nn.Sequential(
nn.Conv2d(hidden_dim, dim, 1),
LayerNorm(dim)
)
def forward(self, x):
b, c, h, w = x.shape
qkv = self.to_qkv(x).chunk(3, dim = 1)
q, k, v = map(lambda t: rearrange(t, 'b (h c) x y -> b h c (x y)', h = self.heads), qkv)
q = q.softmax(dim = -2)
k = k.softmax(dim = -1)
q = q * self.scale
v = v / (h * w)
context = torch.einsum('b h d n, b h e n -> b h d e', k, v)
out = torch.einsum('b h d e, b h d n -> b h e n', context, q)
out = rearrange(out, 'b h c (x y) -> b (h c) x y', h = self.heads, x = h, y = w)
return self.to_out(out)
Diffusion time \(T\)는 각 residual block에 transformer sinusoidal positional embedding이 추가돼서 구분됨
class SinusoidalPosEmb(nn.Module):
def __init__(self, dim):
super().__init__()
self.dim = dim
def forward(self, x):
device = x.device
half_dim = self.dim // 2
emb = math.log(10000) / (half_dim - 1)
emb = torch.exp(torch.arange(half_dim, device=device) * -emb)
emb = x[:, None] * emb[None, :]
emb = torch.cat((emb.sin(), emb.cos()), dim=-1)
return emb
4-1. Sample quality#
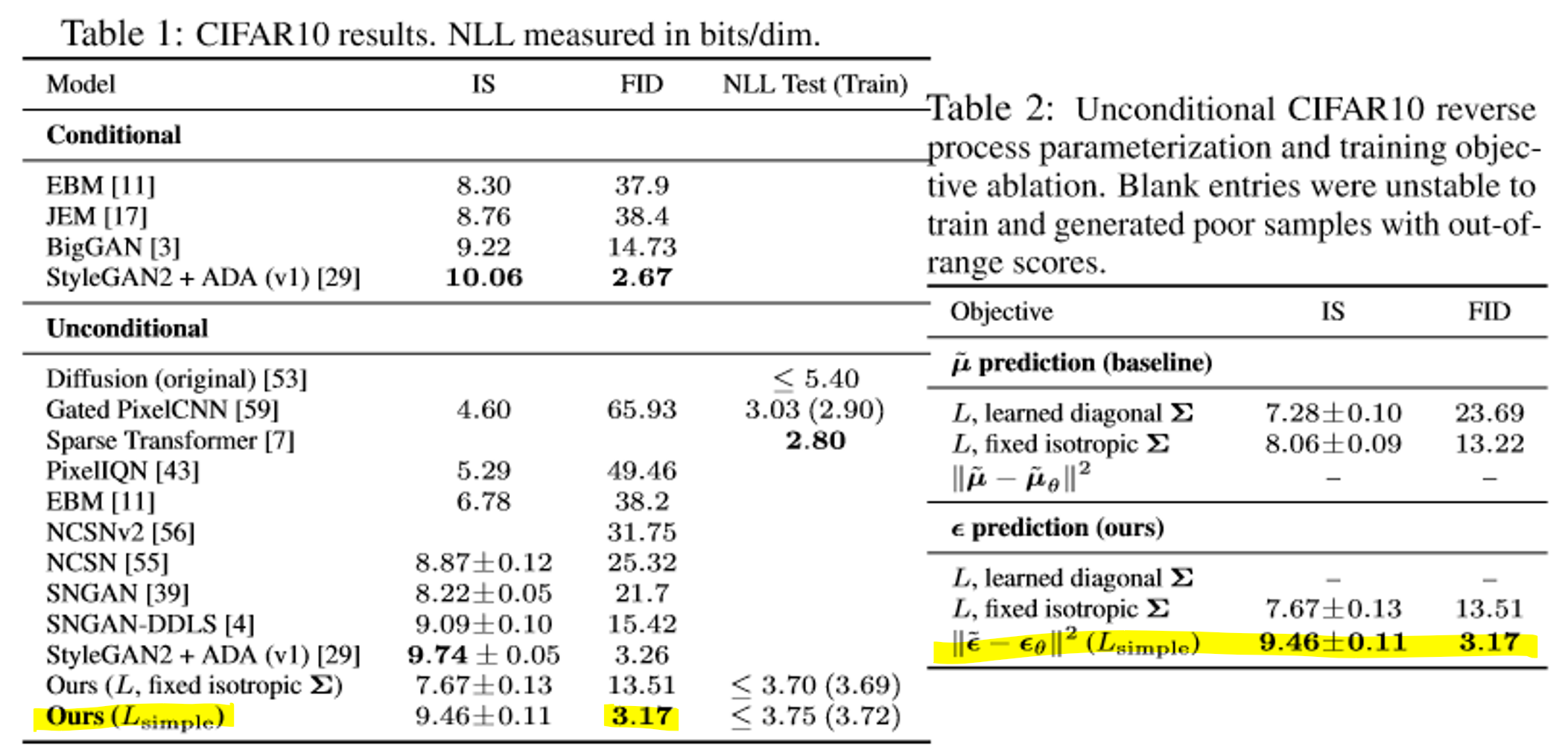
Fig. 21 Train score of DDPM \ (source: https://arxiv.org/abs/2006.11239)#
FID, IS로 metric 계산. Unconditional model인데도 conditional model보다 우월. Codelength에서 차이가 없기 때문에 overfitting의 가능성도 적음.
FID score: 사전 학습된 Inception V3으로 생성된 이미지 집합과 실제 생성하고자 하는 집합 간 클래스 이미지의 분포의 거리를 계산한 metric. 낮을 수록 실제와 유사한 이미지를 생성.
IS(Inception Score): 사전 학습된 Inception V3으로 생성한 이미지에 대해 정확하게 클래스가 나누어지는지, 다양한 클래스를 생성하는지 평가함. 높을 수록 다양한 클래스를 생성.
Unconditional model: 한번 dataset에 학습되면 추가적인 context 없이 image를 생성
Conditional model: Class, label 등의 추가 정보를 받아 image를 생성
\(\mu\)보다 \(\epsilon\)을 계산하는 것이 성적이 좋고, fixed variance를 사용했을 때에도 성능이 감소하지 않음.
4-2. Reverse process parameterization and training objective ablation#
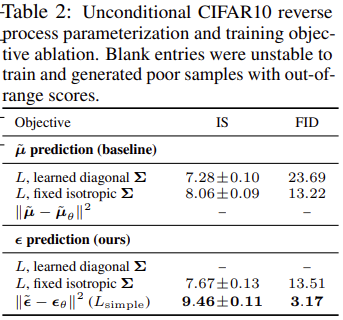
Fig. 22 Comparison between \(\mu\) and \(\epsilon\) \ (source: https://arxiv.org/abs/2006.11239)#
\(\mu\)의 실험 결과를 보면 분산을 고정했을 때 FID에서 성능 차이가 나는 것을 볼 수 있음. 또한 \(\epsilon\)을 사용하면서 Simplified objective를 사용하면 FID, IS가 더 개선됨
