Revisiting CycleGAN for semi-supervised segmentation - arXiv:1908.11569

---

Information

• Title: Revisiting CycleGAN for semi-supervised segmentation, arXiv:1908.11569

• Reference

  • paper : https://arxiv.org/abs/1908.11569

  • code : https://github.com/arnab39/Semi-supervised-segmentation-cycleGAN

• Review By: 김소연

• Edited by: Taeyup Song

• Last updated on Jan. 5, 2022

Background

• Semi-supervised Learning

  • 적은 수의 Labeled dataset $\mathcal{L}=\{(x_i,y_i){\}}_{i=0}^n$와 많은 수의 unlabeled dataset $\mathcal{U}=\{x_i^{\prime }{\}}_{i=0}^m$를 이용하여 특정 task를 수행하는 neural network를 학습

  • Labeled dataset에 대해서는 supervised learning으로 학습 가능, unlabeled dataset으로 regularization.

• GAN (Generative Adversarial Network)

  • Semi-supervised learning 및 unsupervised domain adaptation에서 많이 적용됨.

• CycleGan

  • 반복적으로 입/출력되는 형태로 구성된 GAN

  • domain 간의 image style transfer를 위해 사용됨 → 학습 시 consistency loss를 적용하여 image pair restriction 없이 학습 가능 (domain간의 pair 없이도 학습 가능) → Semi-supervised segmantation task는 labeled set과 unlabeled set의 domain이 다르지 않기 때문에 CycleGAN이 적용되지 않았음.

Contribution

1. CycleGAN의 unpair domain adaptation ability를 이용하여 “unlabeled real image”에서 GT mask와 다시 image로 mapping하는 방법을 학습.

2. Unlabeld dataset에 대해 적용 가능한 unsupervised regularization loss 제안

3. 기존 GAN 적용 semi-supervised semantic segmentation과 달리 CycleGAN을 이용하여 unlabed image와 GT mask간의 cycle consistent mapping을 수행.

Proposed Method

1. CycleGAN for semi-supervised segmentation

• 두 개의 conditional generator와 discriminator로 구성됨.

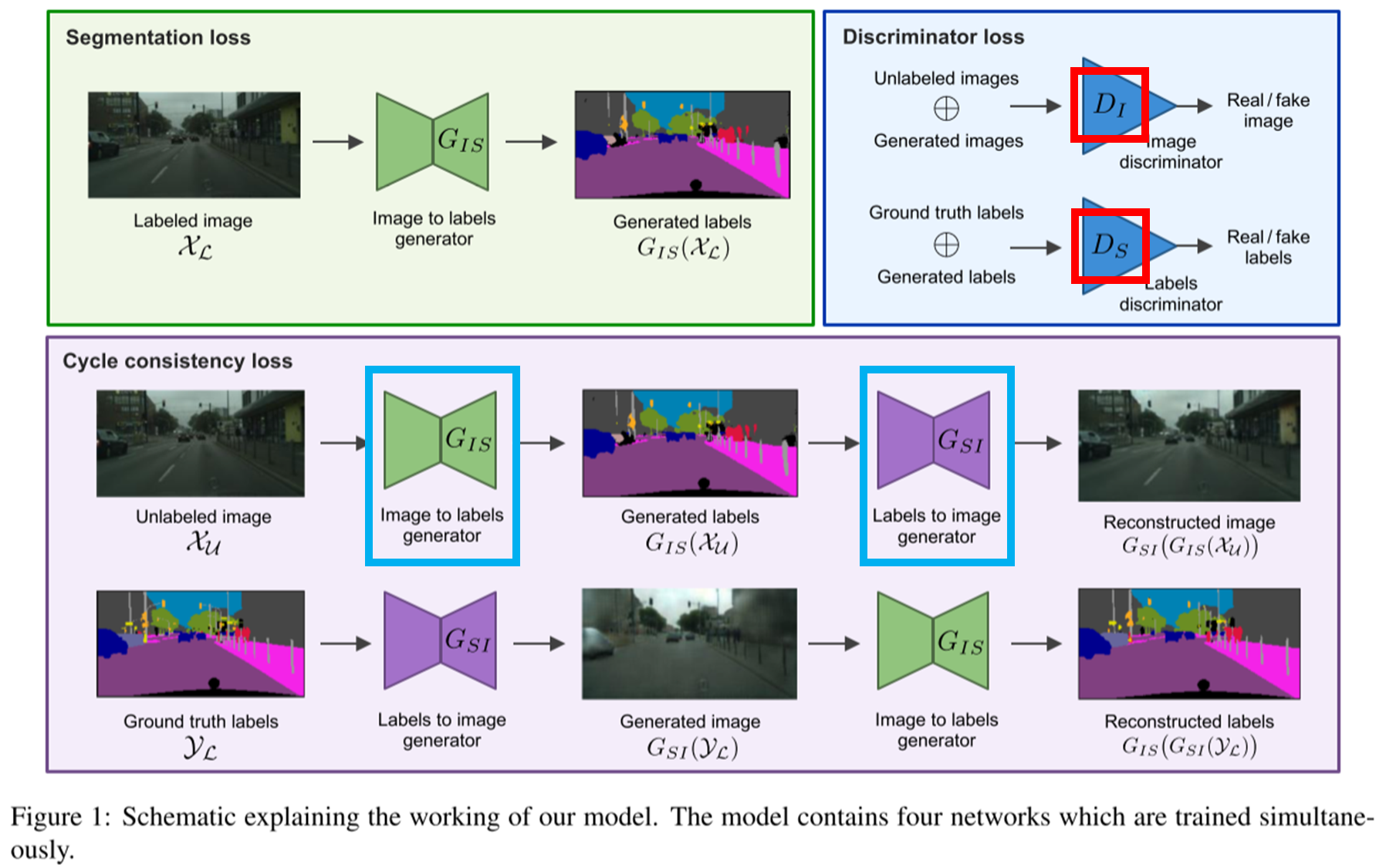
Fig. 127 Schematic explaining the working of proposed model (source: arXiv:1908.11569)

2. Loss functions

$$\begin{array}{r}\begin{array}{rl}{L}_{\text{total}}(G_{IS},G_{SI},D_S,D_I)& =L_{\text{gen}}^S(G_{IS})+{\lambda }_1{L}_{\text{gen}}^I(G_{SI})\\ & +{\lambda }_2{L}_{\text{cycle}}^S(G_{IS},G_{SI})+{\lambda }_3{L}_{\text{cycle}}^I(G_{IS},G_{SI})\\ & -{\lambda }_4{L}_{\text{disc}}^S(G_{IS},D_S)-{\lambda }_5{L}_{\text{cycle}}^I(G_{SI},D_I)\end{array}\end{array}$$

$$\arg \underset{G_{IS},G_{SI}}{max}\arg \underset{D_S,D_I}{max}{L}_{\text{total}}(G_{IS},G_{SI},D_S,D_I)$$

(1) For labeled dataset ${\mathcal{X}}_{\mathcal{L}}$

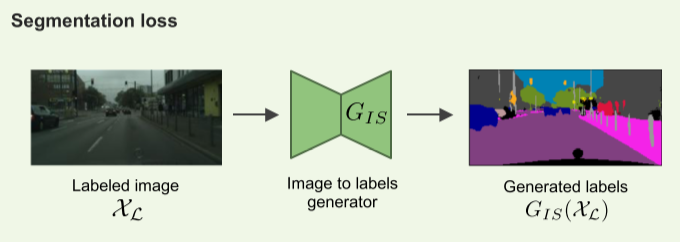
Fig. 128 Segmentation loss (source: arXiv:1908.11569)

• labeled data에 대해서는 pixel level의 classification을 위해 Cross-entropy Loss를 적용

  $$L_{\text{gen}}^S(G_{IS})={\mathbb{E}}_{x,y\backsim {\mathcal{X}}_{\mathcal{L}}{\mathcal{Y}}_{\mathcal{L}}}[\mathcal{H}(y,G_{IS}(x))]$$

  ㅏㅏ여기서 $\mathcal{H}$는 pixel $j$가 $k$ class에 속할 확률을 나타낸다.

• labeled image와 이에 해당하는 GT로 생성된 image간에 loss는 $L2$ norm을 적용

  $$L_{\text{gen}}^I(G_{SI})={\mathbb{E}}_{x,y\backsim {\mathcal{X}}_{\mathcal{L}}{\mathcal{Y}}_{\mathcal{L}}}[||G_{SI}(y)-x|{|}_2^2]$$

(2) Adversarial loss for unlabeled dataset

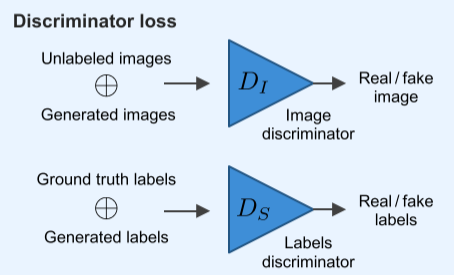
Fig. 129 Adversarial loss (source: arXiv:1908.11569)

• Generator G와 Discriminator D의 compete

• unlabeld image와 GT로 부터 생성된 image를 구분하기 위한 discriminator $D_I$을 위한 adversarial loss는 학습의 용의성을 위해 square loss 적용

  $$L_{\text{disc}}^I(G_{SI},D_I)={\mathbb{E}}_{x\backsim {\mathcal{X}}_{\mathcal{U}}}[(D_I(y{)}^{\prime }-1{)}^2]+{\mathbb{E}}_{y\backsim {\mathcal{Y}}_{\mathcal{L}}}[(D_I(G_{SI}(y)){)}^2]$$

  여기서 $D_I(x)$는 image $x$가 진짜 image일 확률을 나타냄.

• GT labels와 unlabeled image로 부터 생성된 labels를 구분하기 위한 discriminator $D_S$를 위한 adversarial loss 역시 square loss 적용

  $$L_{\text{disc}}^S(G_{IS},D_S)={\mathbb{E}}_{y\backsim {\mathcal{Y}}_{\mathcal{L}}}[(D_S(y)-1{)}^2]+{\mathbb{E}}_{x\backsim {\mathcal{X}}_{\mathcal{U}}}[(D_S(G_{IS}(x^{\prime })){)}^2]$$

  여기서 $D_S(y)$는 label $y$ 가 진짜 mask일 확률을 나타냄.

(3) Cycle consistency loss for unlabeld dataset

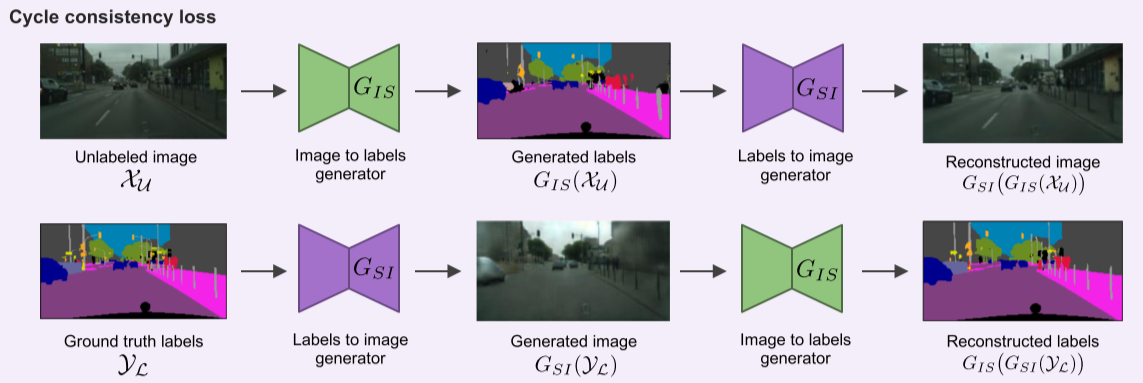
Fig. 130 Cycle consistency loss (source: arXiv:1908.11569)

• Unlabeled data ${\mathcal{X}}_{\mathcal{U}}$를 generator $G_{IS}$로 label을 생성하고, 다시 generator $G_{SI}$를 이용하여 복원한 cycle의 output에 대해 L1 norm 적용 (최종 image를 sharper 하게 만들기 위함)

$$L_{\text{cycle}}^I(G_{IS},G_{SI})={\mathbb{E}}_{x^{\prime }\backsim {\mathcal{X}}_{\mathcal{U}}}[||G_{SI}(G_{IS}(x^{\prime }))-x^{\prime }|{|}_1]$$

• Ground truth로부터 Generator $G_{SI}$로 영상을 생성하고, 다시 generator $G_{IS}$로 labels를 복원하는 cycle의 경우 분류 문제에 해당하므로 cross-entropy 적용

$$L_{\text{cycle}}^S(G_{IS},G_{SI})={\mathbb{E}}_{y^{\prime }\backsim {\mathcal{Y}}_{\mathcal{L}}}[\mathcal{H}(G_{IS}(G_{SI}(y)))]$$

3. Implementation Details

Experimental Result

1. Setting

• Dataset

  • PASCAL VOC 2012 - object / 200x200 pixel로 resize하고 feed 함

  • Cityscapes - scene / 128x256 pixel로 resize

  • ACDC - medical image

• Fully supervised learning으로 학습하여 upper bound performance 구함

• Labeled을 10, 20, 30, 50%를 사용하여 partial baseline 생성

• 이전 SOTA와 비교: Adversarial learning for semi-supervised semantic segmentation

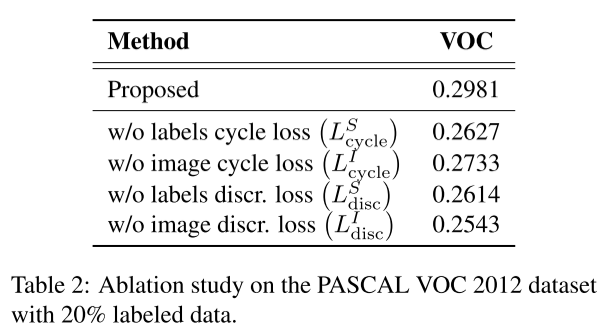
2. Result & discuss

• 20%의 label을 이용한 결과에서 기존 SOTA 방법의 경우 Partial baseline 대비 성능이 저하되지만, 제안된 방법의 경우 더 높은 성능을 나타냄

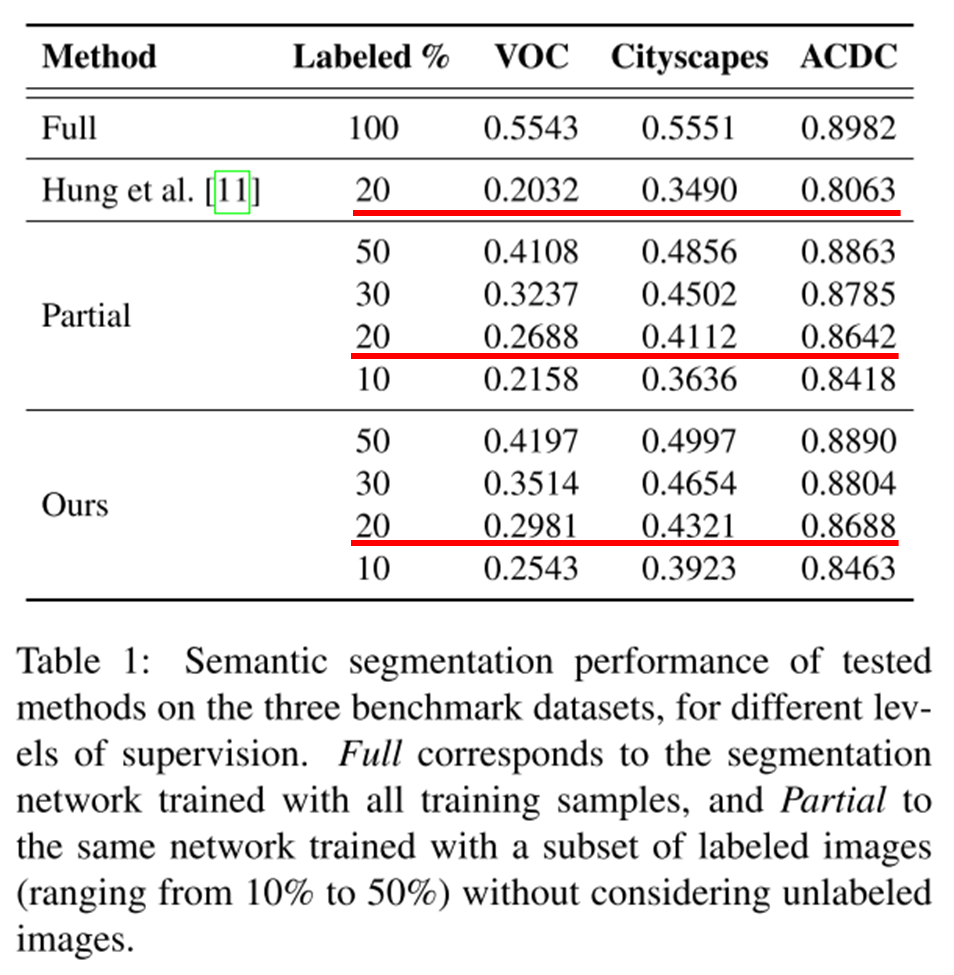
• full supervision을 적용한 baseline 대비 정확도는 낮아도, global semantic과 디테일은 잘 capture한다고 주장

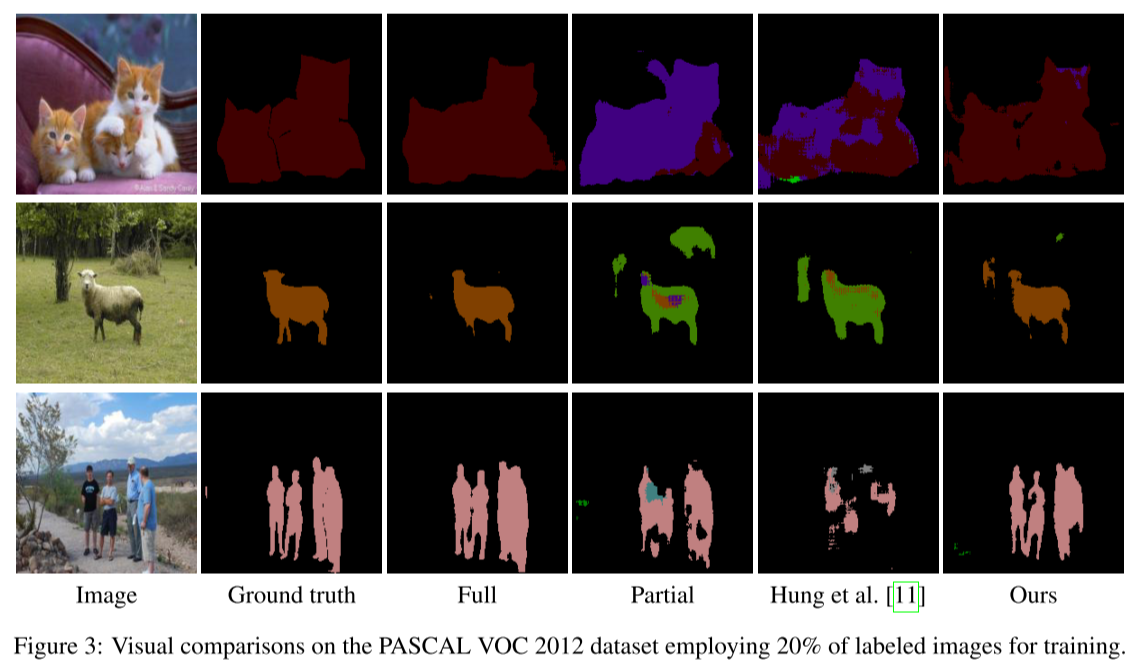
• Cycle loss의 경우 consistency loss on segmentation mask가 성능에 직접적인 영향을 줌. 즉 mask로 image를 생성하고 다시 mask를 생성했을 때, 기존과 동일한지 여부가 중요함

• Discriminator loss의 경우 image discriminator가 더 성능에 큰 영향을 미침. 즉 생성된 이미지인지, real unlabeled 이미지인지 구분하는 판단이 더 중요함.