IAL - IJCV 2020

---

Information

• Title: Weakly-Supervised Semantic Segmentation by Iterative Affinity Learning, IJCV 2020

• Reference

  • Paper: https://arxiv.org/abs/2002.08098 (International Journal of Computer Vision (IJCV), 2020)

  • Code: https://github.com/WangXiang10/IAL (empty repo..)

• Review By: Taeyup Song

• Edited by: Taeyup Song

• Last updated on Jan. 5, 2022

Reference

• Paper: https://arxiv.org/abs/2002.08098 (International Journal of Computer Vision (IJCV), 2020)

• Code: https://github.com/WangXiang10/IAL (empty repo..)

Contribution

• 각 pixel의 Label probability를 학습하기 위한 Unary segmentation network와 이를 refine하기 위한 pairwise affinity network로 구성된 architecture 제안

• 정확한 annotation 없이 신뢰성 높은 pixel affinity를 학습하기 위한 mining confident regions 기법과, 제안한 framework과 equivalent한 energy function을 local min.에 수렴시키기 위해 iteratively하게 학습을 수행하는 방법을 제안.

• PASCAL VOC 2021 및 COCO dataset에서 좋은 성능을 나타냄을 확인.

Proposed Method

1. Architecture

• 각 pixel $x$의 label probability를 구하기 위한 Unary network $F=f(x,W_f)$과 pixel affinity를 학습하기 위한 pairwise network $G=f(x,W_g),G\in {\mathcal{R}}^{N\times N}$ 로 구성됨.

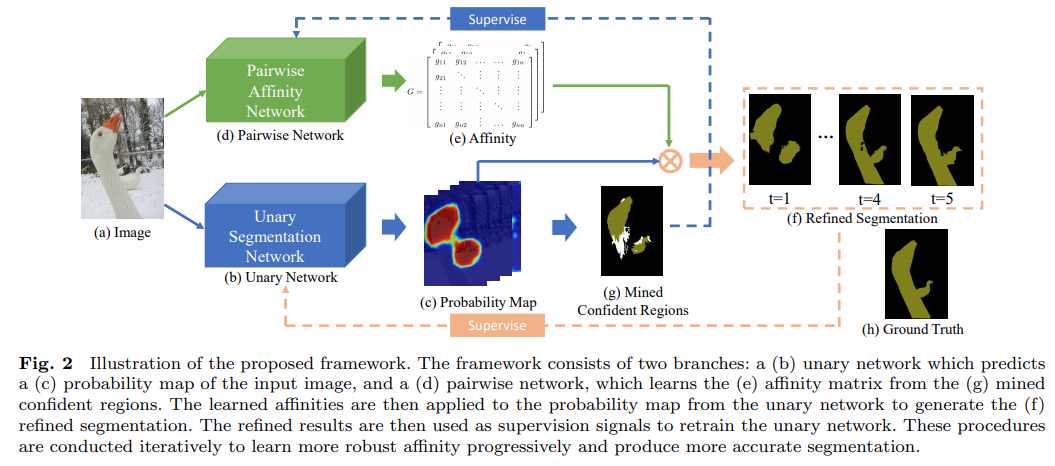
Fig. 97 Illustration of the proposed framework (source: arXiv:2002.08098)

• Unary network를 이용하여 추출한 probability map ${\alpha }_t^u$을 confident region mining을 거친 후 pairwise network의 supervision으로 사용함.

• Pairwise Network를 이용하여 구한 affinity transformation matrix $G$를 이용하여 coarse label probabilities map ${\alpha }_t^u$를 refine 하여 ${\alpha }_t^p=G_t{\alpha }_t^u$를 구한 후 다음 step의 Unary network의 supervision으로 사용.

2. Formulation

• 각 영상을 un-directed weighted graph $\mathcal{G}=(V,E)$로 표현함. → Vertex set $V=\{v_1,...,v_N\}$에서 vertex $v_i$와 $v_j$간의 edge는 weight $w_{ij}$를 갖는다 → 모든 weight는 adjacency matrix $W=(w_{ij}{)}_{i,j=1,...,N}$로 표현 가능하다. → Degree matrix $D$는 degrees $d_1,...d_N$를 element로 갖는 diagonal matrix이다. → Degree는 $d_i=\sum _{j=1}^N{w}_{ij}$으로 표현된다.

• Semantic segmentation을 위해 다음과 같은 energy loss function을 minimize 한다. (유사도가 높은 픽셀이 유사한 label을 같도록 학습함.)

  $${\alpha }^{\ast }=\arg \underset{\alpha }{max}J(\alpha ,W_f,W_g)=\arg \underset{\alpha }{min}{\alpha }^{T}L\alpha$$

  여기서 $\alpha$는 output label의 hidden state, $L=D-W$는 Laplacian matrix이며 ${\alpha }^{T}L\alpha$는 다음과 같이 나타낼 수 있다.

  $$\begin{array}{r}\begin{array}{rl}{\alpha }^{T}L\alpha & ={\alpha }^T(D-W)\alpha \\ & =\sum _{i=1}^N{d}_i{\alpha }_i^2-\sum _{i,j=1}^N{\alpha }_i{\alpha }_j{w}_{i,j}\\ & =\frac{1}{2}(\sum _{i=1}^N{d}_i{\alpha }_i^2-2\sum _{i,j=1}^N{\alpha }_i{\alpha }_j{w}_{i,j}+\sum _{j=1}^N{d}_j{\alpha }_j^2)\\ & =\frac{1}{2}\sum _{i,j=1}^N{w}_{i,j}({\alpha }_i,{\alpha }_j{)}^2\end{array}\end{array}$$

• 본 논문에서는 $\alpha$를 추정하기 위해 similarity metric을 설계하고 최적화하는 방법을 사용하지 않고, EM formulation 기반으로하는 iterative learning method를 적용하여 probability map과 network를 refine하는 방법을 제안함.

• $G=I-D+W=I-L$가 Pairwise network $g$와 pairwise/unary network의 output ${\alpha }_p$와 ${\alpha }_u$를 이용하여 학습가능한 Affinity transformation matrix를 나타낸다면, EM procedure는 다음과 같이 나타낼 수 있다.

  (1) Initialization:

  Class Activation Map에서 얻은 object seed $Y_0$를 이용하여 초기 parameter $\{W_f,W_g{\}}_0$과 unary response map ${\alpha }_0^u$를 얻는다.

  (2) E-Step

  $t$ iteration에서의 $J_t$ loss를 최소화하여 unary probability를 refine 하고,

  $$\frac{\partial J}{\partial {\alpha }_t^u}=L_t{\alpha }_t^u=(1-G_t){\alpha }_t^u$$

  $t$-step에서의 pairwise network의 output ${\alpha }_t^p$를 refine 한다.

  $${\alpha }_t^p={\alpha }_t^u-\mathrm{\Delta }{\alpha }_t^u$$

  unary probability map을 이용하여 pairwise network의 output을 refine한다.

  $${\alpha }_t^p=G_t{\alpha }_t^u$$

  (3) M-Step

  $J_t$가 최소화 되도록 Network $f_{t+1}(x,W_f)$와 $g_{t+1}(x,W_g)$의 parameter $W_f$와 $W_g$를 학습한다. 이때 supervision은 ${\alpha }_t^p$로부터 추출한다.

• Energy function $\mathbf{J}$가 $\alpha$와 network parameter에 모두 미분 가능하기 때문에 EM procedure가 local minimum에 항상 수렴하는 것을 보이는 것은 간단함.

  • For training pairwise network in the $t+1$ step, we consider the softmax cross-entropy loss function

    $$H({\alpha }_{t+1}^u)=-{{\alpha }_{t+1}^u}^{\mathrm{\top }}\log {\alpha }_{t+1}^P$$

    여기서 $\log$함수가 단조 증가 함수이고, pairwise network의 output이 ${\alpha }_{t+1}^p=G_{t+1}{\alpha }_{t+1}^u$이므로

    $$\begin{array}{r}\begin{array}{rl}minH& =-min{{\alpha }_{t+1}^u}^{\mathrm{\top }}{\alpha }_{t+1}^P\\ & =-min{\alpha }_{t+1}^u{G}_{t+1}{\alpha }_{t+1}^u=-min{{\alpha }_{t+1}^u}^{\mathrm{\top }}(I-L_{t+1}){\alpha }_{t+1}^u\end{array}\end{array}$$

    to opt. ${\alpha }_{t+1}^P$is to min. the second term

  $$L_{t+1}=\arg \underset{L_{t+1}^{\ast }}{max}{{\alpha }_{t+1}^u}^{\mathrm{\top }}{L}_{t+1}{\alpha }_{t+1}^u$$

  • ${\alpha }_t^p$를 unary network와 ${\alpha }_{t+1}^u$을 학습하기 위한 supervision으로 사용하는 과정은 M-step으로 나타낼 수 있음.

  • 하지만 pairwise network가 iteration을 반복하며 affinity를 학습하는 과정중에 정확한 supervision이 제공되지 않기 때문에 항상 수렴한고 말할 수 없음.

  • 본 논문에서는 이런 문제를 해결하기 위해 mining된 confidence region $Y_{t+1}$ 적용함. 이를 이용하면 energy function을 낮출 수 있을 것으로 예상함.

  $$Y_{t+1}^{\mathrm{\top }}{L}_{t+1}{\alpha }_{t+1}^u\le {{\alpha }_{t+1}^u}^{\mathrm{\top }}{L}_{t+1}{\alpha }_{t+1}^u$$

2. Training

(1) Unary network

• AffinityNet과 유사한 형태로 구성. DeepLab 구조에 object seed로 CAM을 사용함.

• CAM으로부터 얻은 pseudo label을 이용하여 fully-supervised method와 같은 방법으로 softmax loss를 이용하여 학습함.

• Unary network를 이용하여 추출한 probability map ${\alpha }_t^u$을 confident region mining을 거친 후 pairwise network의 supervision으로 사용함.

(2) Pairwise network

• Spatial Propagation Network(SPN) 구조 적용하여 affinity transformation matrix $G$를 학습

• 정확한 label supervision이 주어지지 않는 상황이기 때문에 segmentation 결과가 정확하지 않아 학습이 잘 안될 수 있음

• 이 문제를 해결하기 위해 segmentation 결과로부터 confident region을 mining한 후 이를 이용하여 학습하는 과정을 거침. pairwise affinity network를 학습하기 위해 softmax loss를 적용함.

  $${\mathcal{L}}_{\alpha }=-Y_t^{\mathrm{\top }}\log {\alpha }_t^p$$

  여기서 $Y_t$는 mining된 confidnet regions임.

• 잘 학습된 affinity matrix는 같은 object 내의 pixel들 처럼 같은 label을 가지는 영역에서는 smooth한 결과를 가지고, 명확한 경계를 가져야 함. 정확한 affinity matrix를 학습하기 위해, superpixel을 이용한 region smoothness loss를 제안함.

  $${\mathcal{L}}_s=||G-G_s|{|}_2^2$$

  여기서 $G$는 affinity matrix를, $G_s$는 각 super-pixel region을 나타냄.

• $G$를 이용하여 coarse label probabilities map ${\alpha }_t^u$를 refine 하여 ${\alpha }_t^p=G_t{\alpha }_t^u$를 구한 후 다음 step의 Unary network의 supervision으로 사용.

(3) Mining Confident Region

Fig. 98 Illustration of mining confident regions (source: arXiv:2002.08098)

• 정확한 label annotation없이 신뢰할 수 있는 affinity matrix를 추출하기 위해 Confidence region을 mining함.

  (1) image에서 분할한 각 super-pixel region $S=\{S_{i,j}\}$로 분할함.

  (2) 어떤 super-pixel의 80% 이상이 unary network의 output에서 class $c$에 matching 된다면 이 superpixel을 class $c$의 sample로 사용함 $\mathcal{D}=\{S,L{\}}_{i,j}$

  (3) 각 class의 sample을 region classification network $f_c^m$를 이용하여 confidence score를 구함.

  (4) segment label과 다른 classification 결과가 나오는 영역을 제거함.

• region classification network $f_c^m$는 mask pooling scheme을 포함하는 fast R-CNN구조를 적용하며, unary network의 label 정보를 supervision하는 cross-entropy loss을 이용하여 학습함.

  $${\mathcal{L}}_m=-\sum _{i,j,c}{L}_{i,j}(c)\log f_c^m(S_{i,j}|{\theta }_m)$$

  여기서 $L_{i,j}$는 one-hot vector로 class c 에 해당하는 element만 1의 값을 가짐.

Experimental Result

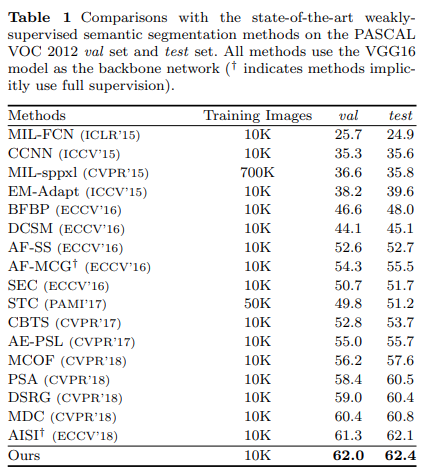
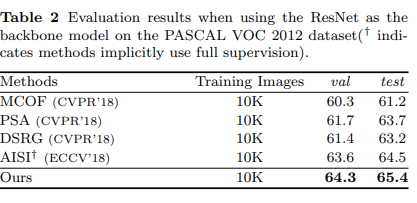
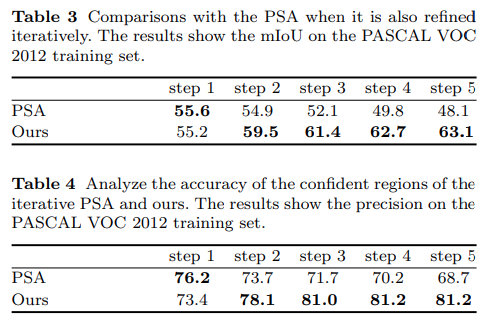
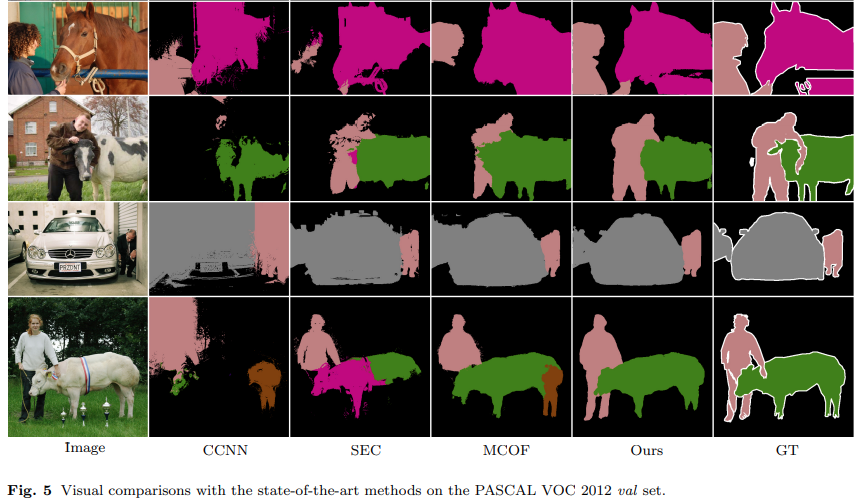
1. Performance Evaluation