U-Net - arxiv 2015#

Information

Contribution#

  • Biomedical image segmentation을 위한 end-to-end architecture 제안.

  • Fully-Convolutional Network을 확장한 expansive(upsample) path와 skip-connection을 적용한 U자 형태의 architecture.

Problem statement#

  • CNN은 주로 classification에 적용됨. Biomedical image processing 같은 경우 localization이 포함된 output이 필요함.

  • Biomedical image 같은 경우 training data의 수가 제한됨. → 적은 training data로 학습할 수 있도록 data argumentation 적용 → Network를 deformation에 invariance하게 학습

  • 많은 cell segmentation task의 경우 동일한 세포(cell)들이 붙어있는 object를 찾아야함. (경계를 찾는 것이 중요함) → weighted loss 적용

Architecture#

(1) FCN 대비 변경점#

  • Full connected layer를 적용하지 않음 (overlap-tile strategy 적용 가능)

  • contracting path part의 feature를 expansive path에서 concatenate. → context와 spatial info.의 trade-off 보완

  • High resolution layer로 context를 propagation하기 위해 expansive(upsampling) path를 다수의 feature channel로 구성.

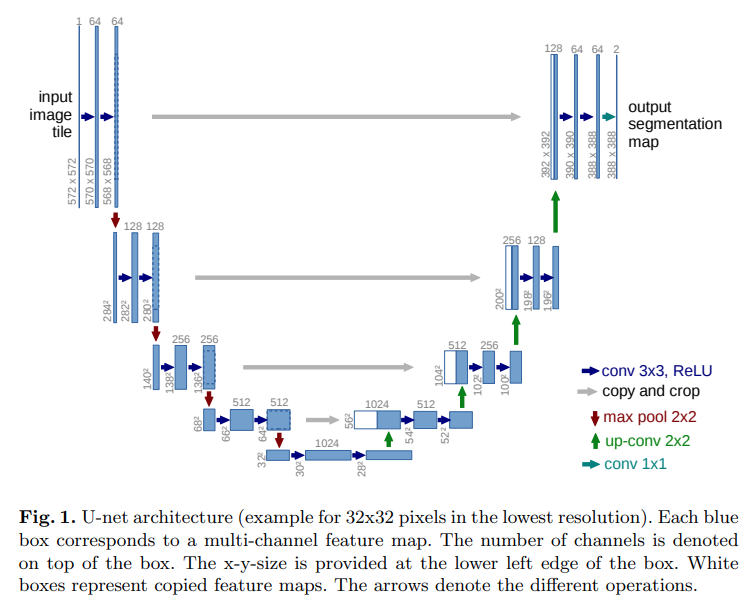
unet1

Fig. 19 U-net architecture (Source: arXiv:1505.04597)#

  • Network 구성 : 3x3 conv.를 연속적으로 배치. down-sample시 max pooling으로 resolution을 반으로 줄이고, channel수를 2배로 늘림. : expansive path의 block은 up-convolution(transposed conv.) 적용한 후 2번의 3x3 conv. 적용하고, contracting path에서 전달된 feature를 crop하여 concatenation 함. : 별도의 pad를 사용하지 않음. →input 대비 output size가 축소됨.

(2) overlap-tile strategy#

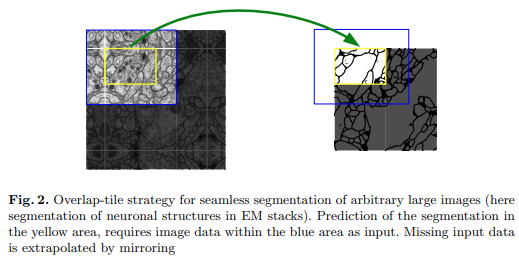
unet2

Fig. 20 Overlap-tile strategy (Source: arXiv:1505.04597)#

  • 큰 영상에 대해 GPU memory 한계 없이 적용가능하기 위해 overlap 방식 사용

  • network 구조상 pad를 적용하지 않아 input/output 크기 차이가 존재하는데, segmentation map이 구해지지 않는 외각 영역에 대해서는 mirroring을 이용한 extrapolation을 적용함.

(3) Training#

  • Optimizer: SGD

  • Energy-function: pixel-wise soft-max over the final feature map with cross entropy loss function

    \[E=\sum_{\mathbf{x}\in\Omega} w(\mathbf{x})\log(p_{l(\mathbf{x})}(x))\]

    여기서 \(p_l\)은 \(l\) class에 대한 softmax 값 \(l:\Omega\rightarrow\{1,...,K\}\)

  • Biomedial image 분야의 segmentation task는 동일한 label을 가지는 세포(cell)등의 군집을 잘 분리해야 한다. → 각 cell 사이의 경계를 잘 찾아야 함.

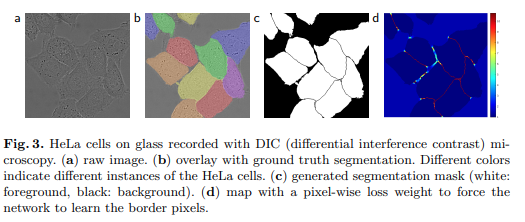
unet3

Fig. 21 HeLa cells on glass recordede with DIC microscopy (Source: arXiv:1505.04597)#

  • 학습 데이터에서 각 픽셀의 class 분포를 weight map으로 구한 후 학습에 반영.

    \[w(\mathbf{x})=w_c(\mathbf{x})\cdot \left( -\frac{(d_1(\mathbf{x})+d_2(\mathbf{x}))^2}{2\sigma^2}\right)\]

    여기서 \(w_c\)는 class frequencies를 나타내는 weight map 이고, \(d_1\)은 nearest cell간의 거리, \(d_2\)는 두번째 nearest cell간의 distance이다.

Experimental Result#

unet4.png