SOLOv2 - NeurIPS 2020#

Information

Problem Statement and Contribution#

  • SOLO[]는 별도의 bounding box prediction 및 pixel간의 pairwise relation 정보 없이 instance mask를 구하는 framework으로 다음과 같은 한계가 존재한다.

    • Inefficient mask representation and learning

    • 좋은 퀄리티의 mask predictions을 얻기 위해 resolution이 충분하지 않음.

    • 느린 mask NMS 속도

  • 본 논문에서는 SOLO architecture를 개선을 목표로 convolution kernel learning 및 이를 이용한 feature learning기법과 inference 속도 개선을 위한 fast NMS 기법을 적용한 SOLOv2 구조를 제안한다.

Proposed Method#

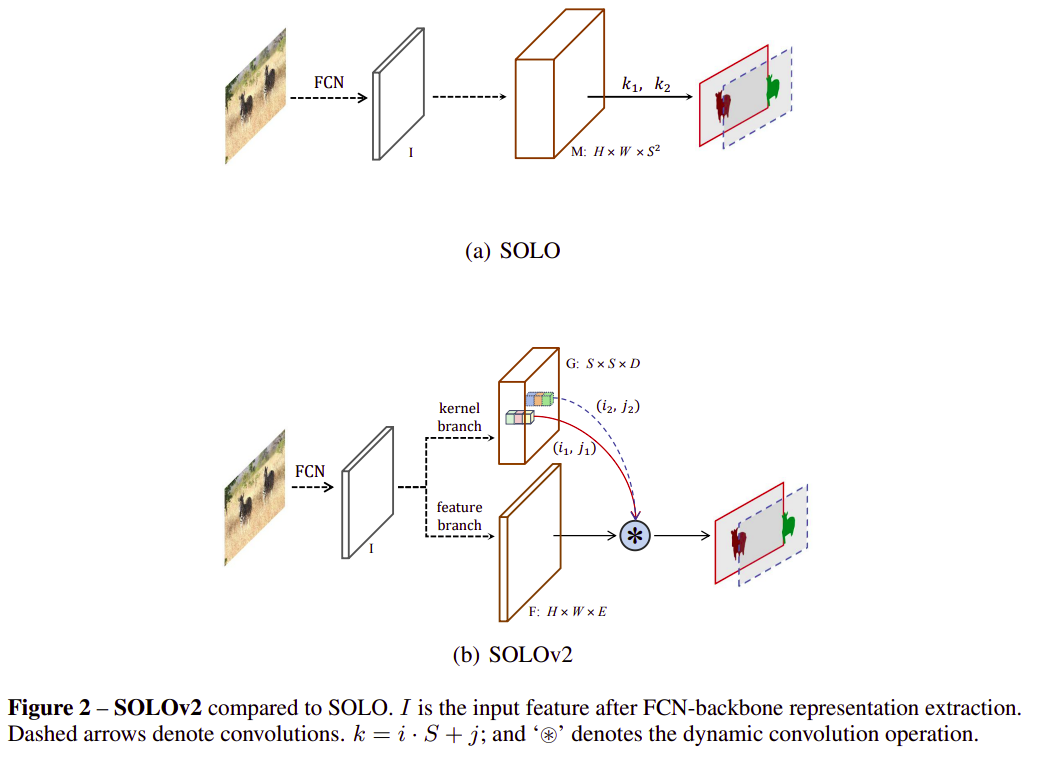
20211013181442

Fig. 51 SOLOv2 campared to SOLO (source: arXiv:2003.10152)#

1. Dynamic Instance Segmentation#

  • SOLO architecture의 경우 \(S^2\) channel의 instance mask를 생성한다. 입력 영상에 대해 FPN(feature pyramid network)을 이용하여 \([H \times W \times E]\) dimension의 feature를 추출 후 이를 다시 \(S^2\) channel로 변환하는 과정을 거친다.

  • Pyramid feature중 특정 level에서 추출한 feature가 주어질 때 \(F \in \mathbb{R}^{H \times W \times E}\) 위 과정을 수식으로 표현하면 다음과 같다.

    \[ M_{i,j}=G_{i,j}*F \]

    여기서 \(G_{i,j}\in\mathbb{R}^{1\times1\times E}\)는 \((i,j)\) grid에 적용되는 convolution kernel를 나타낸다. \(m_{i,j}\in \mathbb{R}^{H\times W}\)은 최종 mask이며 \((i,j)\) grid에 하나의 Instance의 중심좌표가 포함된 경우를 나타낸다.

  • SOLO model은 inference/training 과정에서 위 연산 과정을 거치는데, memory를 필요로 하고 특히나 큰 resolution에 대해서는 높은 computation cost가 필요한 문제가 있다.

  • 대부분의 경우에서 영상안의 instance는 분리되어 있기 때문에 mask \(M\)연산하는 과정에 \(S^2\) kernel을 적용하는 것은 효율적이지 않다.

  • 만약 \(F\)와 \(G\)를 따로 학습할 수 있다면, dynamic하게 사용함으로 segmentation의 location을 효과적으로 찾을 수 있다.

(1) Mask Kernal Branch (\(G\))

  • Backbone과 FPN이 주어지면, 모든 level의 pyramid feature에 대해 feature mask kernel \(G\)를 predict한다.

    • \(I\) 번째 pyramid 에서 추출한 feature \(F_I\in\mathbb{R}^{H_I\times W_I \times C}\)가 입력되면 grid cell (\(S \times S \times C\))로 resize한다.

    • 4번의 3x3 convolution과 마지막 \((3\times 3\times D)\) kernel을 이용한 convolution을 적용하여, 최종 kernel \(G\)를 얻는다. 첫번째 convolution은 CoordConv를 적용하여 coordinates를 normalize한다.

    • 이 과정을 통해 각 level의 feature 마다 D-dimension의 아웃풋이 생성되며, \(3\times 3\) kernel을 predict하는 경우 \(D=9E\)가 되도록 구성한다. (최종 output에는 activation function을 적용하지 않는다.)

(2) Mask feature branch (\(F\))

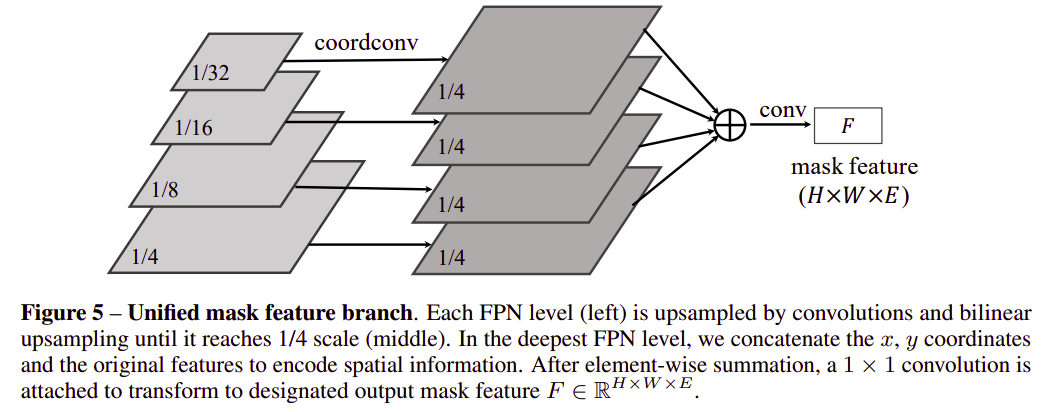
20211013181442

Fig. 52 Unified mask feature branch in SOLOv2 (source: arXiv:2003.10152)#

  • SOLOv2 model은 mask kernel과 feature가 각각 학습되는 구조로, mask feature branch를 2가지 case로 구성할 수 있다.

    • Kernel branch와 함께 head 구성하여 각 pyramid lavel에 대해 feature 추출

    • 모든 level의 feature를 fusion 후 unified mask feature 추출

  • 논문에서는 실험을 통해 unifed mask featrure를 추출하는 것이 효율적임을 확인하고 적용하였다.

    • 입력의 1/4 size로 bilinear upsampling 후 sum한 후 수 차례의 convolution 연산을 수행하여 feature를 추출한다.

    • 이 과정에서 정확한 위치 정보를 전달하기 위해 가장 깊은 level의 pyramid feature에 대해 CoordConv. 를 적용하여 normalized 된 coordinate 정보를 전달한다. 이는 position sensitivity와 predicting instance-aware features를 위해 중요하다.

20211013181442

Fig. 53 Mask Feature Behavior (source: arXiv:2003.10152)#

  • Fig. 53은 64 output channels (\(E=64\))일 때 최종 feature map을 나타낸다.

  • 황색 box의 mask feature와 같이 특정 position에 맞는 영역이 activation되는 feature와 흰색 box와 같이 모든 instance 혹은 배경에만 activation되는 mask feature를 모두 추출함을 알 수 있다.

(3) Forming Instance Mask

  • 각 \((i,j)\) grid cell에 대해 먼저 mask kernel \(G_{i,j,:}\in\mathbb{R}^{D}\) 를 계산한다.

  • Instance mask를 구하기 위해 mask kernel을 feature \(F\)와 convolution연산을 수행한다.

  • 최종적으로 각 prediction level에 대해 \(S^2\)개의 mask를 계산한 후 NMS를 적용하여 최종 instance segmentation 결과를 도출한다.

(4) Learning and inference

  • Focal loss + Dice loss를 적용

    \[ \mathcal{L}=\mathcal{L}_{\text{cate}}+\lambda\mathcal{L}_{\text{mask}} \]

    여기서 \(\mathcal{L}_{\text{cate}}\)는 semantic category classficiation을 위한 Focal Loss이며, \(\mathcal{L}_{\text{mask}}\)는 mask prediction을 위한 Dice Loss이다.

  • Inference 과정에서 입력된 영상에 대해 backbone과 FPN을 거쳐 category score \(\mathbf{p}_{i,j}\)를 구한 후, 첫번째 confidence threshold 0.1을 적용하여 낮은 confidence인 prediction 결과를 제거한다. 최종적으로 threshold 0.5를 적용하여 최종 soft mask를 도출한다.

2. Matric NMS#

  • 기존 NMS의 느린 속도를 개선하기 위해 soft-NMS [22]방법을 변형한 방법을 제안함.

    • Soft-NMS의 경우 overlay된 detection score에 단조 감소 함수 \(f(\text{iou})\)를 적용한다. 이때 높은 IoU를 가지는 경우 score 감소폭을 크게하여 작은 score threshold로 제거할 수 있도록 한다.

    • 하지만, 이런 과정은 Greedy NMS와 마찬가지고 병렬 processing이 불가능한 한계가 있다.

  • 이를 보완하기 위해 Matrix NMS 방법을 제안한다. Matrix NMS의 decay factor는 다음 두가지 factor에 영향을 받는다.

    • Prediction score에 의한 penalty →Soft-NMS와 마찬가지로 단조 감소 함수 \(f(\text{iou}_{i,j})\)로 쉽게 계산 가능

    • mask prediction \(m_i\)가 제거될 확률

      • 보통 확률은 IoU와 양의 상관관계를 가짐을 이용한다.

      • 논문에서는 가장 많이 겹친 두 prediction에 대해 제거될 확률의 근사값을 바로 구한다.

      \[ f(\text{iou},i)=\min_{\forall{s_{k}}>s_i}f(\text{iou}_{k,i}) \]

    • 최종 decay factor를 다음과 같이 구한다.

      \[ \text{decay}_j=\min_{\forall{s_{k}}>s_i}\frac{f(\text{iou}_{i,j})}{f(\text{iou}_{,i})} \]

      여기서 감소 함수는 linear \(f(\text{iou}_{i,j})=1-\text{iou}_{i,j}\)와 Gaussian \(f(\text{iou}_{i,j})=\exp\left( -{\text{iou}^2_{i,j}}/{\sigma}\right)\) 를 적용할 수 있다.

    • 최종적으로 decay factor를 이용하여 score를 update한다.

    \[ s_j=s_i\cdot\text{decay}_j \]

  • Implementation

    def matrix_nms(scores, masks, method=’gauss’, sigma=0.5):
    # scores: mask scores in descending order (N)
    # masks: binary masks (NxHxW)
    # method: ’linear’ or ’gauss’
    # sigma: std in gaussian method

    # reshape for computation: Nx(HW)
    masks = masks.reshape(N, HxW)

    # pre−compute the IoU matrix: NxN
    intersection = mm(masks, masks.T)
    areas = masks.sum(dim=1).expand(N, N)
    union = areas + areas.T − intersection
    ious = (intersection / union).triu(diagonal=1)

    # max IoU for each: NxN
    ious_cmax = ious.max(0)
    ious_cmax = ious_cmax.expand(N, N).T
    # Matrix NMS, Eqn.(4): NxN
    if method == ’gauss’: # gaussian
        decay = exp(−(iousˆ2 − ious_cmaxˆ2) / sigma) else: # linear
        decay = (1 − ious) / (1 − ious_cmax)
    # decay factor: N
    decay = decay.min(dim=0)
    return scores ∗ decay

Experimental Result#

1. Implementation Details (SOLO와 동일)#

  • Optimization: Stochastic gradient descent (SDG), synchronized SGD over 8 GPUs

  • Batch Size: 16

  • Learning Rate

    • 초기 learning rate는 0.01로 설정되며, 27 epoch에서 10으로 나누고(lr=0.001), 33번때 epoch에서 다시 한번 10으로 나눈 값을 사용함 (lr=0.0001).

    • Weight decay 0.0001, momentum 0.9를 적용함.

  • ImageNet Pre-trained weight 적용

  • 짧은 image side의 크기가 640~800 pixel 사이로 random하게 sampling하는 scale jitter를 적용함.

2. Main Result#

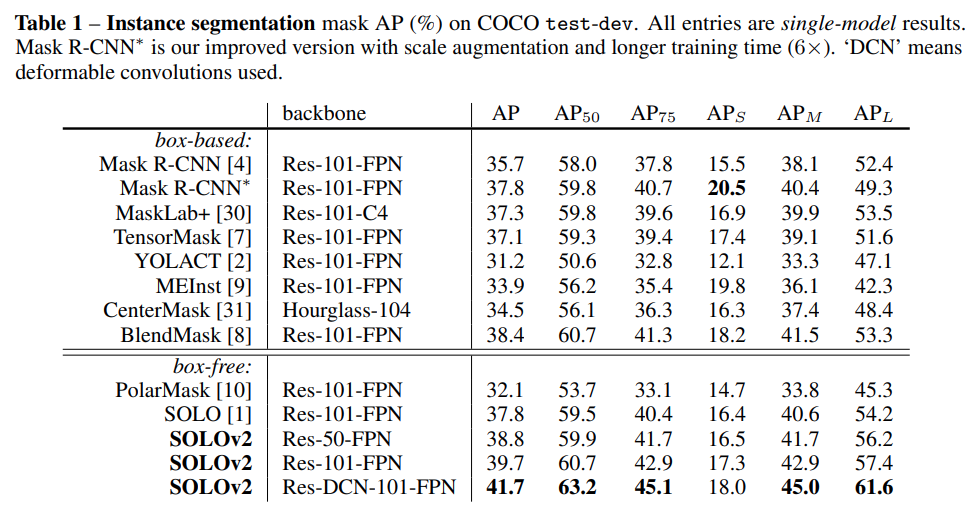
  • MS COCO test-dev에서 성능을 비교한 결과, ResNet-101 backbone을 사용한 SOLOv2가 mask AP 39.7%로 기존 방법모드 높은 성능을 나타냄을 확인할 수 있다.

  • 다만 small object에 대한 성능 \(AP_S\) 의 경우 저자가 학습한 mask R-CNN 보다 낮은 성능을 나타내었다.

solov2_4.png

  • COCO dataset에서 속도-성능 trade-off를 나타내보면, 기존 instance segmentation 방법대비 SOLO v2 모델이 빠른 inference time 대비 높은 성능을 나타냄을 알 수 있다.

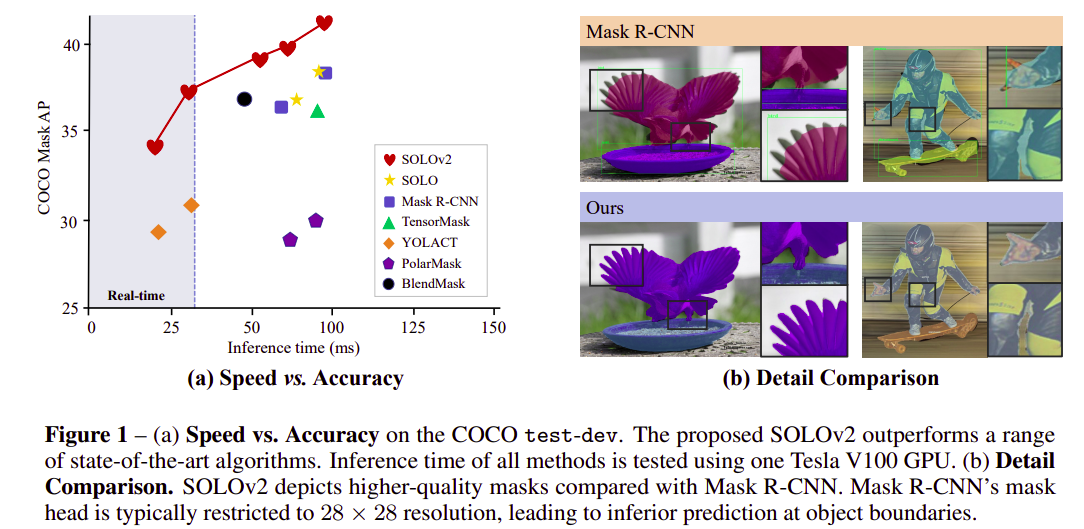
solov2_5.png solov2_6.png

3. Ablation Experiment#

  • Kernel shape을 비교한 결과 1x1와 3x3 kernel을 적용했을 때 거의 동등한 성능을 나타냄. (Table 3 (a)

  • CoordConv를 적용하여 normalized 된 coordinate 정보를 kernel과 feature에 모두 추가했을 때 성능 개선이 있음. (Table 3 (b))

  • 제안된 Matrix-NMS가 기존 방법대비 빠른 속도와 높은 AP를 가짐을 확인함. (Table 3 (c))

  • Mask feature learning 과정에서 각 pyramid level별로 head로 구성하는 것 보다, unified representation을 적용한 경우가 더 높은 성능을 나타냄. (Table 3 (d))

solov2_7.png