Semi-supervised Semantic Segmentation with Directional Context-aware Consistency - CVPR 2021

---

Information

• Title: Semi-supervised Semantic Segmentation with Directional Context-aware Consistency, CVPR 2021

• Reference

  • paper : https://jiaya.me/papers/semiseg_cvpr21.pdf (CVPR 2021)

  • code : https://github.55860.com/dvlab-research/Context-Aware-Consistency

• Review By: Chanmin Park

• Edited by: Taeyup Song

• Last updated on Jan. 5, 2022

Problem statement

• full label을 생성하기에 time-consuming이 많이 듬

• 기존의 supervised learning은 적은 data로 인해서 overfitting이 많이 일어남 (Fig. 1 참조)

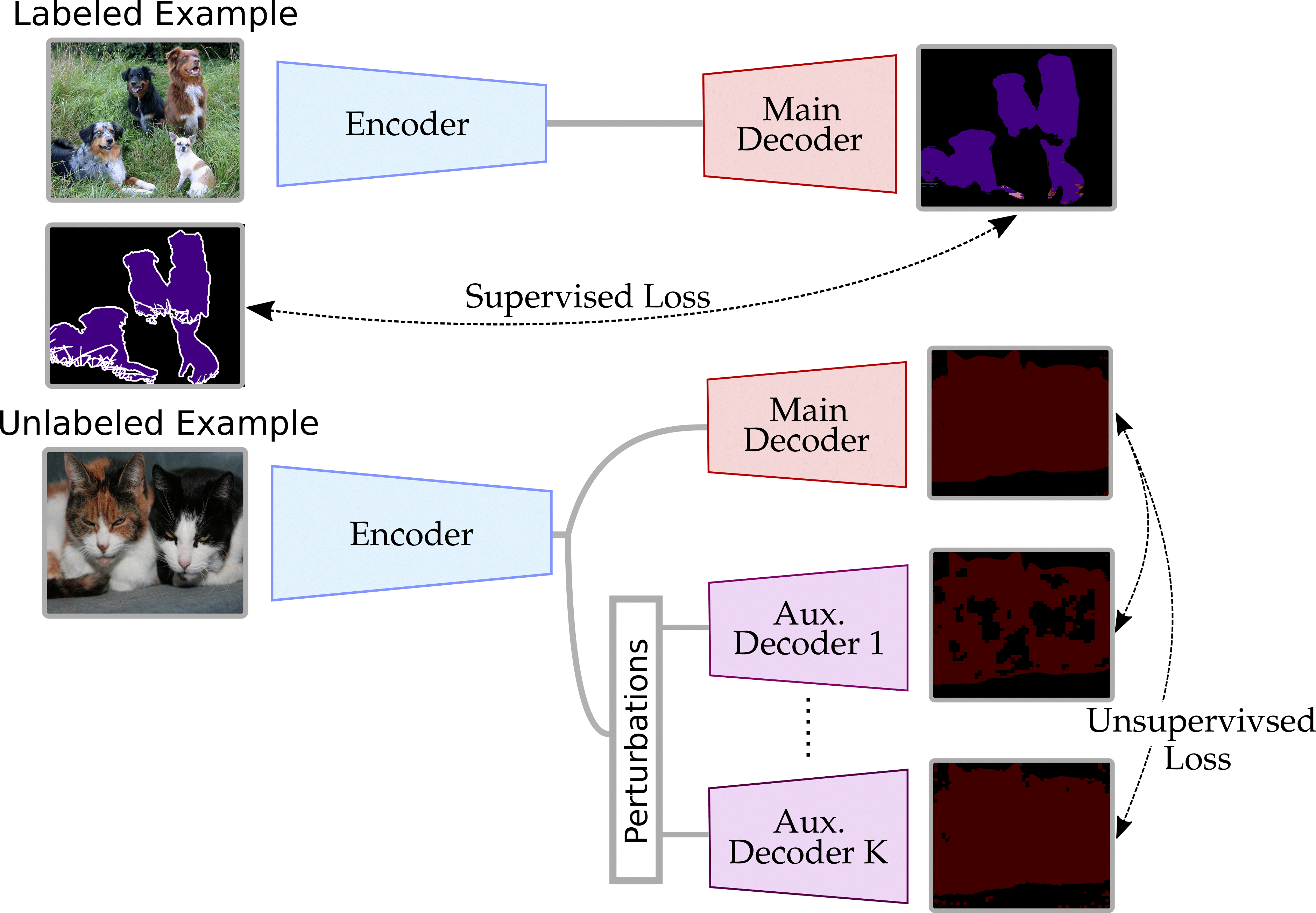
Fig. 121 1/8 의 label만 사용하여 학습한 model을 GradCAM으로 visualization을 한 결과. (source: arXiv:2106.14133)

• 기존의 segmentation은 receptive field의 한계로 인해서 context information에 대해서 학습을 하지 않음.

Contribution

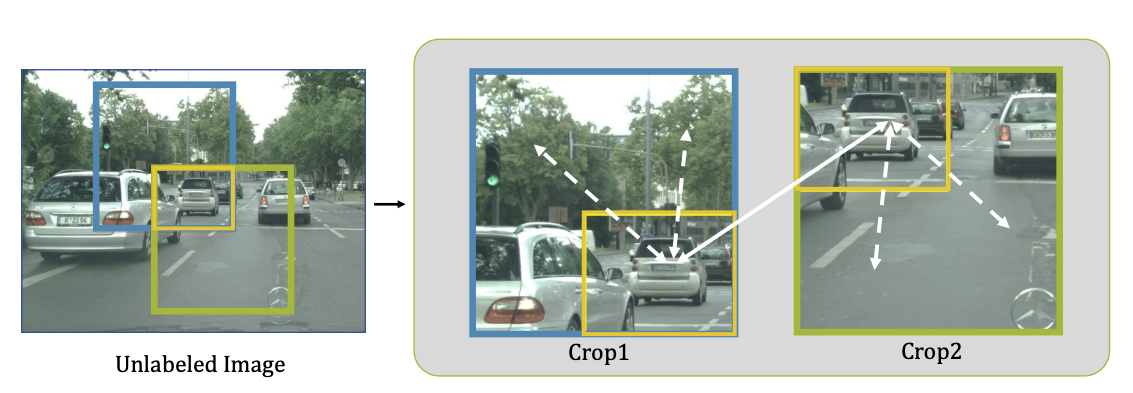
Fig. 122 Crop1 and Crop2 are randomly cropped from the same image with an overlapping region. (source: arXiv:2106.14133)

• 위의 그림과 같이 label이 있는 부분을 overlapping을 해서 patch데이터간의 consistency 를 주어지며 이른 context aware consistency라고 명시함

• contextual alignment를 주기 위해서 directional contrastive loss를 제시함 이는 pixel wise로 cosine similarity 주게 되는 방법을 의미함.

• 데이터의 sampling 하는 새로운 방법을 제시함으로 negative sample와 ambiguous한 postive sample을 filtering함

Related work

• Semi-Supervised Semantic Segmentation with Cross-Consistency Training, CVPR 2020

  • semi supervised 의 대표적인 방법중에 하나로 permutation 다양하게 부여하여 invaraince를 높임

  • weakly label이 필요없는 장점이 있음.

  

  Fig. 123 CCT architecture (source: arXiv:2003.09005)

Proposed Method

1. motivation

Fig. 124 Visual comparison between contextual augmentation (I and II) and low-level augmentation (I and III) (source: arXiv:2106.14133)

• 노란색으로 되어진 overlapping region에서 weak augmentation (gaussian noise, color jitter) 했을때와 다른 위치의 patch를 구헀을때의 이미지임

• 두번째 행에서 보는 바와 feature에서 T-SNE를 적용하면 weak augmentation에서는 feature space가 전혀 바뀌지 않음.

2 Network

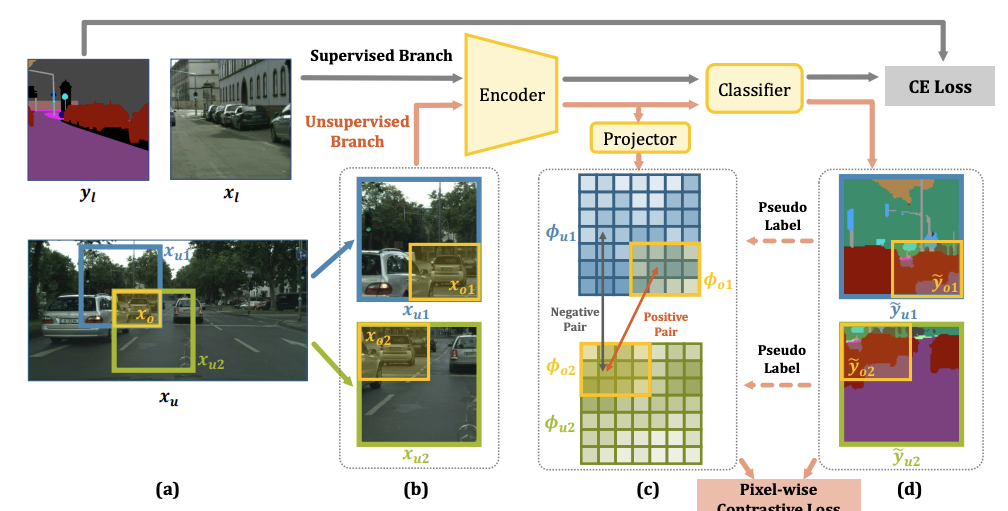
Fig. 125 Overview of framework (source: arXiv:2106.14133)

• label,target image, unlabel image: $y_t,x_t,x_u$

• overlapping image(w/label),non overlapping image(wo/label) : $x_{u1},x_o,x_{u2}$

• project feature : $\Phi$

2.1 Context-aware Consistency

• low level feature projection을 시킨후 upsacaling을 한결과를 label의 영역간의 pixel wise constrative loss를 적용시켜줌

• 저자는 low level에서 feature를 projection을 시키면 좀더 context에 대해서 학습할수있다고 ablation result를 통해서 보여줌

2.2 Directional Contrastive loss(DC loss)

• 기존의 contrastive loss의 경우 MSE를 적용하여주었지만 저자는 cosine simliarity를 통해서 문제를 접근함.

  

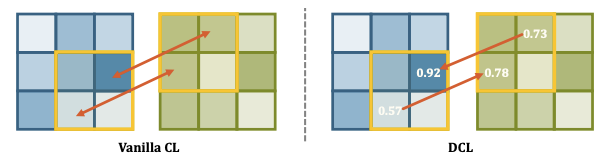
  Fig. 126 Comparison between vanilla CL and DCL (source: arXiv:2106.14133)

  $$l_{dc}^b({\varphi }_{o_1},{\varphi }_{o_2})=-\frac{1}{N}\sum _{h,w}{\mathcal{M}}_d^{h,w}\cdot \log \frac{r({\varphi }_{o_1}^{h,w},{\varphi }_{o_2}^{h,w})}{r({\varphi }_{o_1}^{h,w},{\varphi }_{o_2}^{h,w})+\sum _{{\varphi }_n\in {\mathcal{F}}_{\mathcal{u}}}r({\varphi }_{o_1}^{h,w},{\varphi }_n)}$$
  $${\mathcal{M}}_d^{h,w}=\mathbf{1}\{maxC(f_{o_1}^{h,w}<maxC(f_{o_2}^{h,w})\}$$
  $${\mathcal{L}}_{dc}^b=l_{dc}^b({\varphi }_{o_1},{\varphi }_{o_2})+l_{dc}^b({\varphi }_{o_2},{\varphi }_{o_1})$$

• 식에서 있듯이 overlapping이 된 영역끼지의 cosine similarity를 loss를 줄여줌

• 반면에 negative pair에 관해서는 분모로 두어서 더 similarity를 멀게 만듬

• $M_d^{h,w}$ 같은 경우 pixel단위로 target되어지는 pixel이 source pixel보다 크면 loss를 계산함.

2.3 sampling Strategies

• negative pair의 양을 조절해야되기때문에 pseudo label에서 negative의 prediction을 값을 통해서 filtering을 함

  $${\tilde{y}}_{ui}=\arg maxC(f_{ui})i\in \{1,2\}$$
  $$l_{dc}^{b,n,s}({\varphi }_{o_1},{\varphi }_{o_2})=-\frac{1}{N}\sum _{h,w}{\mathcal{M}}_d^{h,w}\cdot \log \frac{r({\varphi }_{o_1}^{h,w},{\varphi }_{o_2}^{h,w})}{r({\varphi }_{o_1}^{h,w},{\varphi }_{o_2}^{h,w})+\sum _{{\varphi }_n\in {\mathcal{F}}_{\mathcal{u}}}{\mathcal{M}}_{n,1}^{h,w}\cdot r({\varphi }_{o_1}^{h,w},{\varphi }_n)}$$

• Positive 에서도 prediction의 낮은 값의 경우 $\gamma$를 통해서 filtering을 적용하여줌

$$l_{dc}^{b,ns,pf}({\varphi }_{o_1},{\varphi }_{o_2})=-\frac{1}{N}\sum _{h,w}{\mathcal{M}}_{d,pf}^{h,w}\cdot \log \frac{r({\varphi }_{o_1}^{h,w},{\varphi }_{o_2}^{h,w})}{r({\varphi }_{o_1}^{h,w},{\varphi }_{o_2}^{h,w})+\sum _{{\varphi }_n\in {\mathcal{F}}_{\mathcal{u}}}{\mathcal{M}}_{n,1}^{h,w}\cdot r({\varphi }_{o_1}^{h,w},{\varphi }_n)}$$

$${\mathcal{M}}_{d,pf}^{h,w}={\mathcal{M}}_{\mathcal{d}}^{\mathcal{h}\mathcal{,}\mathcal{w}}\cdot \mathbf{1}\{maxC(f_{o_2}^{h,w})>\gamma \}$$

• 이러한 방법들을 바탕으로 CAM을 통해서 weak-superivsed도 문제를 접근할수 있음

Experimnets