2.2 Project transformation

2D projective geometry는 projective plane ${\mathbb{P}}^2$ 의 projectivies라고 알려져있는 transformation들에서 invariant한 특성들의 연구입니다.

Projection은 ${\mathbb{P}}^2$ 에서의 한점에서 ${\mathbb{P}}^2$ 안의 한 점으로 반대로 projection 할 수 있으며, 선에서 선으로 projection 됩니다.

Projectivity

Projectivity는 역이 성립하는 평면 ${\mathbb{P}}^2$ 에서 ${\mathbb{P}}^2$로의 mapping projection $h$를 의미합니다. 예를 들어, ${\mathbf{x}}_{\mathbf{1}}$, ${\mathbf{x}}_{\mathbf{2}}$ ${\mathbf{x}}_{\mathbf{3}}$같은 선 상에 존재한다면, $h({\mathbf{x}}_{\mathbf{1}})$, $h({\mathbf{x}}_{\mathbf{2}})$, $h({\mathbf{x}}_{\mathbf{3}})$도 같은 선 상에 존재합니다.

이러한 projection을 collineation, projective transformation, homography 라고도 부릅니다.

Projective transformation

Plane의 Projective transformation은 homogeneous 3-vector에서 non-singular 3x3 행렬에 의해 표현되는 선형 변환입니다.
$\left(\begin{array}{c}x{\prime }_1\\ x{\prime }_2\\ x{\prime }_3\end{array}\right)=\left[\begin{array}{ccc}{h}_{11}& h_{12}& h_{13}\\ h_{21}& h_{22}& h_{23}\\ h_{31}& h_{32}& h_{33}\end{array}\right]\left(\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right)$
또는, 간결하게 ${\mathbf{x}}^{\prime }\mathbf{=}\mathtt{H}\mathbf{x}$ 로 표현할 수 있습니다.

$H$는 homogeneous matrix 이기 때문에 상수를 곱해도 동일합니다. scale factor로 나눠주면 결과적으로 동일하기 때문입니다. 따라서 H의 dof는 8이며, scale factor를 제외한 나머지 원소들입니다.

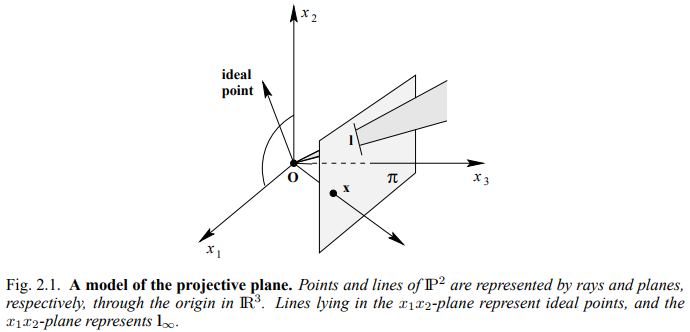
Projective transformation은 동일한 projective space 내 모든 plane을 투영적으로 동등하게 projection 시키며, 모든 이 사영 속성들은 invariant 합니다. 위 그림 2.1의 ray 모델에서 projective transformation은 ${\mathbb{R}}^3$의 linear transformation 입니다.

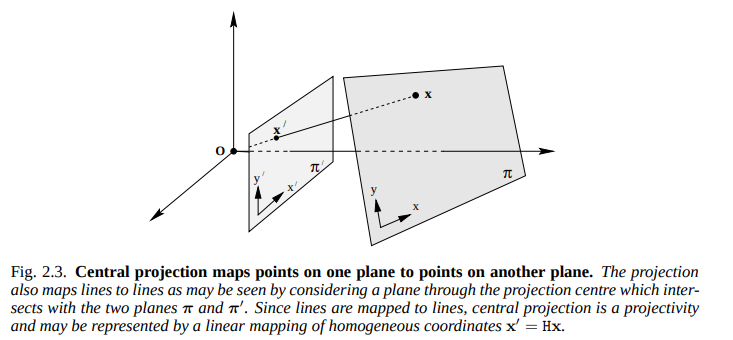
Mapping of planes

위 그림 2.3은 동일한 projective space에 존재하는 두 평면이 존재할 때 원점 $\mathbf{O}$과 이어진 ray가 있다고 할 때, 동일 ray 위에 존재하는 점들은 같은 점이라는 것을 보여줍니다. 좌표 시스템이 평면에서 정의되고 있으면서, 그 점이 homogeneous coordinate로 표현된다면, Central projeciton은 ${\mathbf{x}}^{\prime }\mathbf{=}\mathbf{Hx}$로 표현할 수 있습니다.

Removing the projective distortion from a perspective image

Perspective 이미지에서 real world에서의 모양은 왜곡됩니다. 위 그림 2.4의 a는 그 예를 보여줍니다. 위에서 얘기했듯, projective projection의 dof는 8입니다. 따라서 4개의 점을 지정해서 projective projection을 정의할 수 있는데, 여기서는 원래는 평행한 두 직선을 지정해 다시 평행해지도록 transformation을 적용해 사영 왜곡을 삭제했습니다.

$x^{\prime }=\frac{x_1^{\prime }}{x_3^{\prime }}=\frac{h_{11}x+h_{12}y+h_{13}}{h_{31}x+h_{32}y+h_{33}},y^{\prime }=\frac{x_2^{\prime }}{x_3^{\prime }}=\frac{h_{21}x+h_{22}y+h_{23}}{h_{31}x+h_{32}y+h_{33}}.$

$x^{\prime }(h_{31}x+h_{32}y+h_{33})=h_{11}x+h_{12}y+h_{13}$

$y^{\prime }(h_{31}x+h_{32}y+h_{33})=h_{21}x+h_{22}y+h_{23}$

homogeneous 좌표로부터 inhomogeneous 좌표로의 변형은 위와 같이 표현할 수 있습니다. 각 포인트는 H원소에 대한 두 등식으로 표현될 수 있습니다.

위와 같은 equation을 통해 projective transformation에 의해 점이 이동할 위치를 계산할 수 있습니다. 점을 선정할 때 주의할 점은 세 점이 같은 직선 위에 존재하면 안 된다는 것입니다. 이렇게 계산된 projective transformation $\mathbf{H}$는 non-singular matrix로 역행렬이 존재하며, 이것을 적용하면 반대로 돌아갈 수 있습니다.

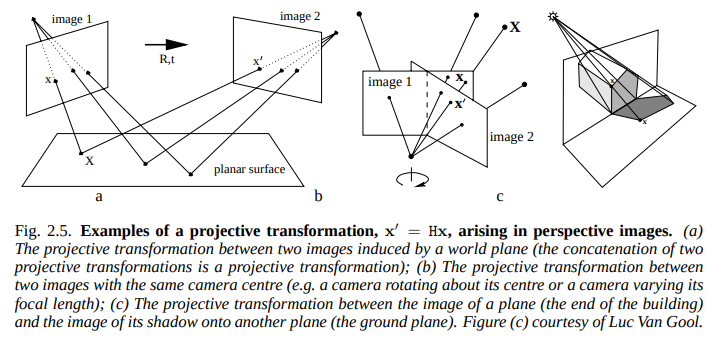
그림 2.5는 ${\mathbf{x}}^{\prime }\mathbf{=}\mathbf{HX}$ 수식으로 생길 수 있는 다양한 projective transformation의 예를 보여줍니다. 이 각각의 transformation은 이후 다른 Chapter들에서 학습합니다.

Reference

1. Multiple view geometry in computer vision chapter 2.3