ㅤ안녕하세요, 가짜연구소 Groovy Graph 팀의 한수민입니다. 이 글은, ‘The PageRank Citation Ranking Bringing Order to the Web’ 논문을 읽고, 정리한 글 입니다.

ㅤ이 글은 Reference 자료들을 참고하여 정리하였음을 먼저 밝힙니다. 혹시 내용중 잘못된 점이나 보완할 점 있다면 댓글로 알려주시면 감사하겠습니다. 그럼 시작하겠습니다.

---

목차

1. Reference
2. PageRank의 배경
3. PageRank 정의 & 개념
   1. 웹 그래프
   2. PageRank란?
   3. PageRank에 대한 직관
4. Simple PageRank
   1. 투표 (vote) 관점
   2. random walk 관점
   3. 관점 정리
   4. Simple PageRank 계산
   5. Simple PageRank의 문제점
5. Simple PageRank
   1. Spider trap과 Dead end 문제 해결
   2. Simple PageRank 계산 예시
6. PageRank의 결과
   1. Convergence Properties
7. + 질문

---

1 Reference

• CS224W 4. Link Analysis: PageRank
• 그래프와 추천 시스템
• [Paper Review] The PageRank Citation Ranking: Bringing Order to the Web

---

2 PageRank의 배경

• 구글 이전의 검색 엔진은, 사용자가 입력한 키워드에 의존하여 웹 페이지를 반환했습니다.
• 하지만 이러한 키워드에 의존하는 검색 엔진에는 취약점이 있습니다. 악성 웹 페이지들이 검색 엔진을 속여, 사용자의 검색 키워드에 상관 없이, 사용자들을 자신의 페이지로 오게 만들기 쉬웠습니다.
  • (e.g.) “운동화” 판매자가 자신의 페이지에, 자신의 “운동화” 판매와 상관 없는 내용들을 (e.g., 영화, 음악, …), 보이지 않게 (바탕색과 똑같은 색깔의 글씨로) 가득 적어놓으면, 검색 엔진은 “영화”를 키워드로 검색에도 “운동화” 판매 페이지를 보여줍니다.
• 구글은, 검색 엔진의 품질을 향상시키기 위해, PageRank 기술을 도입했습니다.

---

3 PageRank 정의 & 개념

3.1 웹 그래프

• 웹은 directed graph로 표현할 수 있습니다.
  • node: 웹 페이지
  • edge: 하이퍼링크

3.2 PageRank란?

• 구하고 싶은, 웹 페이지의 점수(중요성, 신뢰성)를 rank라고 하겠습니다.
• PageRank는 웹 그래프를 이용하여 웹 페이지의 rank를 계산하는 알고리즘입니다.

• PageRank의 가정 (underlying assumption)
  • 참조가 많이 된 페이지는 참조가 적게 된 페이지보다 중요합니다.
  • 중요한 페이지가 참조한 페이지는 중요합니다.

3.3 PageRank에 대한 직관

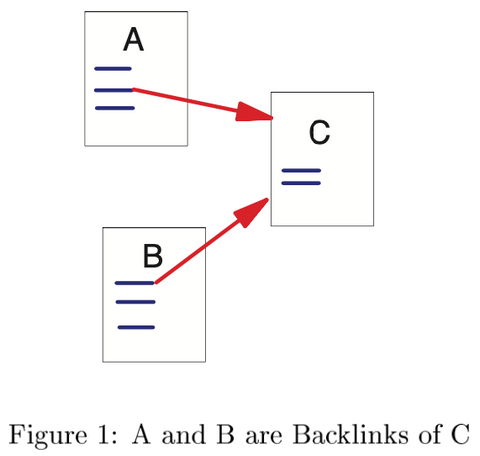
• 그림 2에서,
  • 웹 페이지 B의 rank는 가장 높습니다.
    • B가 다른 웹 페이지들로부터 참조가 많이 됐기 때문입니다.
  • 웹 페이지 C의 rank는 2번째로 높습니다.
    • C는 참조가 1번 밖에 안 됐지만, rank가 가장 높은 B가 참조하고 있기 때문에, C의 rank도 높습니다.
  • 보라색 페이지들은 참조가 없지만, PageRank의 어떤 기법(teleport) 때문에, rank가 0이 아닙니다.

---

4 Simple PageRank

4.1 투표 (vote) 관점

• PageRank는 투표를 통해 중요한 웹 페이지를 찾습니다.
• 이 때, 웹 페이지 (node)는 투표를 받는 대상이고, 투표는 하이퍼링크 (edge)를 통해 이루어집니다.
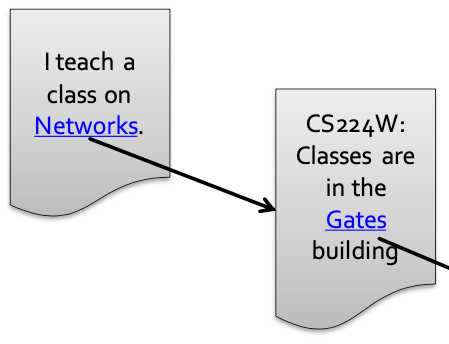
  • (e.g.) 그림 3에서, “I teach a class on Networks.” 페이지는 하이퍼링크를 통해 “CS224W: Classes are in the Gates building” 페이지에 투표했다고 생각할 수 있습니다.

• 다음과 같이 표현을 정리할 수 있습니다.
  • 웹 페이지 A가 웹 페이지 B를 참조한다
  • == 웹 페이지 A에서 웹 페이지 B로 가는 하이퍼링크가 있다
  • == 웹 페이지 B에는 웹 페이지 A로부터 오는 backlink (in-edge, in-link)가 있다
  • == 웹 페이지 A가 웹 페이지 B를 투표했다
  • == 웹 페이지 A의 작성자가 웹 페이지 B를 신뢰할 수 있다고 판단했다

• 즉, 어떤 페이지에 backlink (in-edge, in-link)가 많을수록, 그 페이지를 신뢰할 수 있다고 말할 수 있습니다.

---

• PageRank의 투표 방식은 다음과 같습니다.
  1. 모든 웹 페이지는 투표 점수(rank)를 갖고 있습니다.
     • 보통, 맨 처음에는 모두 같은 투표 점수를 갖고 있습니다.
     • 우리는 중요하고, 신뢰가 가는 페이지가 다른 페이지들보다 투표 점수(rank)가 높기를 바랍니다.
  2. 웹 페이지는 자신이 갖고 있는 투표 점수를, 투표하려는 웹 페이지에게 똑같이 나누어서 투표합니다.
     • == 자신이 갖고 있는 투표 점수를, out-degree로 나누어, 나눠진 점수가 씌여진 종이를, out-edge가 향하는 웹 페이지에게 보냅니다.
  3. 투표가 끝난 뒤, 각 웹 페이지는 자신이 받은 투표 점수을 모두 더하여, 자신의 새로운 투표 점수를 계산합니다.

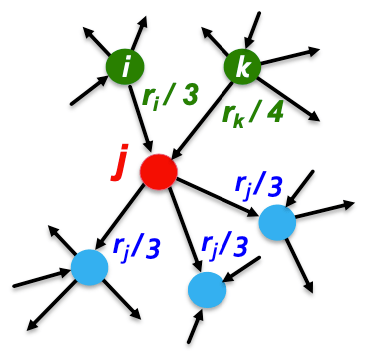
• (e.g.) 투표 점수 계산 방법 (그림 4)
  • 페이지 $j$는, 자신의 투표 점수 (rank) $r_j$를 out-degree 수로 나눈 $\displaystyle \frac{r_j}{3}$를, out-edge가 가리키는 페이지에게 보냅니다.
  • 페이지 $j$의 새로운 투표 점수 (rank)는, in-edge를 통해 받은 투표 점수들의 합이므로, $\displaystyle r_j = \frac{r_i}{3} + \frac{r_k}{4}$ 가 됩니다.

• 단순하게 각 페이지들의 backlink 수를 세지 않고, 위와 같은 투표 방식을 도입한 이유는, 악성 웹 페이지들이 서로를 참조하여, backlink 수를 높게 만드는 조작을 하지 못하게 하기 위함입니다.

• 각 웹 페이지의 rank의 정의는 다음과 같습니다.
  • $d_i$: out-degree

\[r_j = \sum_{i \rightarrow j}^{} \frac{r_i}{d_i}\]

• 우리가 구하고 싶은 것이 웹 페이지의 rank인데, rank를 구하기 위해 rank를 사용하는 것이 이상하게 보일 수 있습니다.
  • 이 부분은 “4.4 Simple PageRank의 계산”에서 다루도록 하겠습니다.

4.2 random walk 관점

• random walk를 통해, 웹을 서핑하는 웹 서퍼가 있다고 가정합시다.
• random walk를 통해, 웹을 서핑하는 웹 서퍼의 행동은 다음과 같습니다.
  • 웹 서퍼는, 현재 웹 페이지에 있는 여러 하이퍼링크 중 하나를 uniform한 확률로 선택해 이동합니다.

• $p (t)$ 라는 벡터가 있다고 가정합시다.
  • $p (t)$의 $i$번째 값 $p_i (t)$은, 웹 서퍼가 $t$ 번째 방문한 웹 페이지가 웹 페이지 $i$일 확률입니다.
• $p (t)$ 는 웹 페이지에 대한 확률 분포가 됩니다.

• $p (t)$로부터 $p (t+1)$을 계산할 수 있습니다.

\[p_j (t+1) = \sum_{i \rightarrow j}^{} \bigg ( p_i(t) \times \frac{1}{d_i} \bigg ) = \sum_{i \rightarrow j}^{} \frac{p_i (t)}{d_i}\]

• 웹 서퍼가 이 과정을 무한히 반복하고 나면, 즉 $t$가 무한히 커지면, 확률 분포 $p(t)$는 수렴하게 됩니다.
  • 다시 말하면, $p(t) = p(t+1) = p$ 가 성립하게 됩니다.
  • 수렴한 확률 분포 $p$는 stationary distribution이라고 부릅니다.
  • 이렇게 되면, 식을 다음과 같이 바꿀 수 있습니다.

\[p_j (t+1) = \sum_{i \rightarrow j}^{} \frac{p_i (t)}{d_i} \quad\quad \Rightarrow \quad\quad p_j = \sum_{i \rightarrow j}^{} \frac{p_i}{d_i}\]

4.3 관점 정리

• 투표 관점에서 정의한 rank
  • == random walk 관점에서의 stationary distribution
  • (== 논문 수식)

• 투표 관점에서 정의한 rank
  • $d_i$: out-degree

\[r_j = \sum_{i \rightarrow j}^{} \frac{r_i}{d_i}\]

• random walk 관점에서 정의한 stationary distribution

\[p_j = \sum_{i \rightarrow j}^{} \frac{p_i}{d_i}\]

• 논문 수식
  • $u$: 웹 페이지
  • $B_u$: 페이지 $u$를 가르키는 페이지의 집합
  • $F_u$: 페이지 $u$가 가르키는 페이지의 집합
  • $N_u = |F_u|$: 페이지 $u$가 가르키는 페이지의 수 (== 페이지 $u$에서 나가는 edge 수)
  • $c$: normalization factor (모든 웹 페이지의 총 rank가 일정하도록)

\[R(u) = c \sum_{v \in B_u}^{} \frac{R(v)}{N_v}\]

4.4 Simple PageRank의 계산

4.4.1 Simple PageRank의 matrix formulation

• PageRank 식은 다음과 같이 matrix 형태로 나타낼 수 있습니다.

\[r = M \cdot r\]

• $r$ : rank 벡터
• $M$ : column stochastic adjacency matrix
  • $N_u = |F_u|$: 페이지 $u$가 가르키는 페이지의 수 (== 페이지 $u$에서 나가는 edge 수)

\[M_{u, v} = \begin{cases} \frac{1}{N_u}, & \text{if there is an edge from} \; v \; \text{to} \; u \\ 0, & \text{otherwise} \end{cases}\]

---

• 예제를 통해서 자세히 알아보도록 하겠습니다.

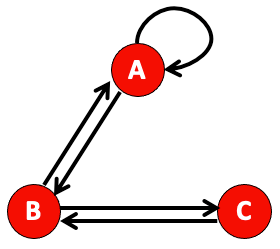
1. 각 페이지가 얻는 rank를 연립 방정식으로 표현해보겠습니다.
   • $\displaystyle r_a = \frac{1}{2} r_a + \frac{1}{2} r_b$
   • $\displaystyle r_b = \frac{1}{2} r_a + r_c$
   • $\displaystyle r_c = \frac{1}{2} r_b$

2. (1)의 연립 방정식을 matrix 형태로 나타내보겠습니다.

   \[\begin{bmatrix} r_a \\ r_b \\ r_c \\ \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & 0\\ \frac{1}{2} & 0 & 1\\ 0 & \frac{1}{2} & 0 \\ \end{bmatrix} \begin{bmatrix} r_a \\ r_b \\ r_c \\ \end{bmatrix}\]
3. (2)의 matrix 식을 간단하게 $r = Mr$로 나타낼 수 있습니다.
   • 이 때, $M$은 column stochastic matrix입니다.
     • column stochastic matrix는
       • matrix의 모든 값들이 음수가 아니여야 합니다.
       • 각 column의 합이 1입니다.

\[r = \begin{bmatrix} r_a \\ r_b \\ r_c \\ \end{bmatrix} , \quad M = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} & 0\\ \frac{1}{2} & 0 & 1\\ 0 & \frac{1}{2} & 0 \\ \end{bmatrix}\]

4.4.2 Simple PageRank의 eigenvector formulation

• $r = M \cdot r$ 식을 다시 쓰면, $M \cdot r = 1 \cdot r$ 이 됩니다.
• $M \cdot r = 1 \cdot r$ 식을 보면,
  • $M$의 eigenvalue가 1이고, eigenvector가 $r$이라고 할 수있습니다.

• eigenvector $r$을 구하기 위해, power iteration을 사용할 수 있습니다.

4.4.3 Power Iteration

• rank 계산에는 power iteration을 사용합니다.

• power iteration은 3단계로 구성됩니다.
  1. 각 웹 페이지 $i$의 rank $r_{i}^{(0)}$를 동일하게 $\displaystyle r_{i}^{(0)} = \frac{1}{\text{웹 페이지의 수}}$로 초기화합니다.

  2. 아래 식을 이용하여, 각 웹 페이지의 rank를 갱신합니다.

     \[r_{j}^{(t+1)} = \sum_{i \rightarrow j}^{} \frac{r_i^{(t)}}{d_i}\]
  3. rank가 수렴하면 ($r^{(t)} \approx r^{(t+1)}$) 종료하고, 아니면 (2)로 돌아갑니다.
     • rank가 수렴하면, $r^{(t)} \approx r^{(t+1)}$을 rank 벡터로 사용합니다.

4.5 Simple PageRank의 문제점

4.5.1 power iteration은 수렴을 보장하나요? (Spider trap 문제)

• power iteration은 수렴을 보장하지 않습니다.

• spider trap은 들어오는 edge는 있지만, 나가는 edge는 없는 node 집합을 말합니다.
• spider trap에 의해서 power iteration은 수렴하지 않는 문제가 발생합니다.

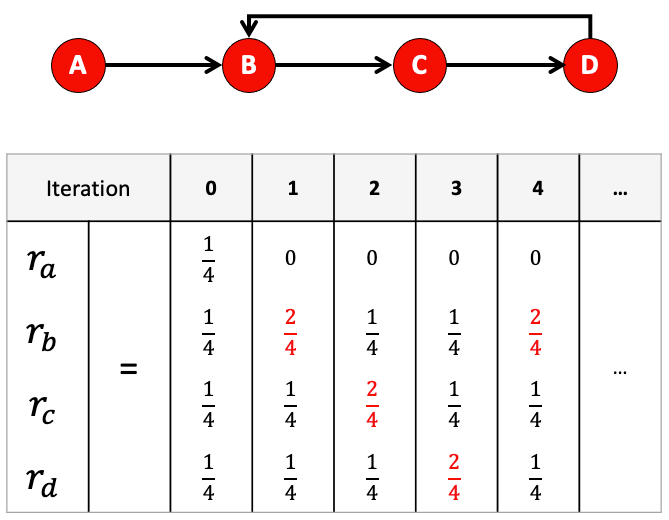
• (e.g.) spider trap 문제가 발생하는 경우 (그림 6)
  • iteration 1과 iteration 4의 rank는 동일합니다. 따라서, rank가 수렴하지 않고, 무한히 반복됩니다.

• 해결 방법은 아래에서 알아보도록 하겠습니다.

4.5.2 “합리적인” rank로 수렴하는 것을 보장하나요? (Dead end, Dangling link 문제)

• power iteration은 “합리적인” rank로의 수렴을 보장하지 않습니다.

• dead end는 들어오는 edge는 있지만, 나가는 edge는 없는 node를 말합니다.
• dead end에 의해서 power iteration이 합리적인 rank로 수렴하지 않는 문제가 발생합니다.

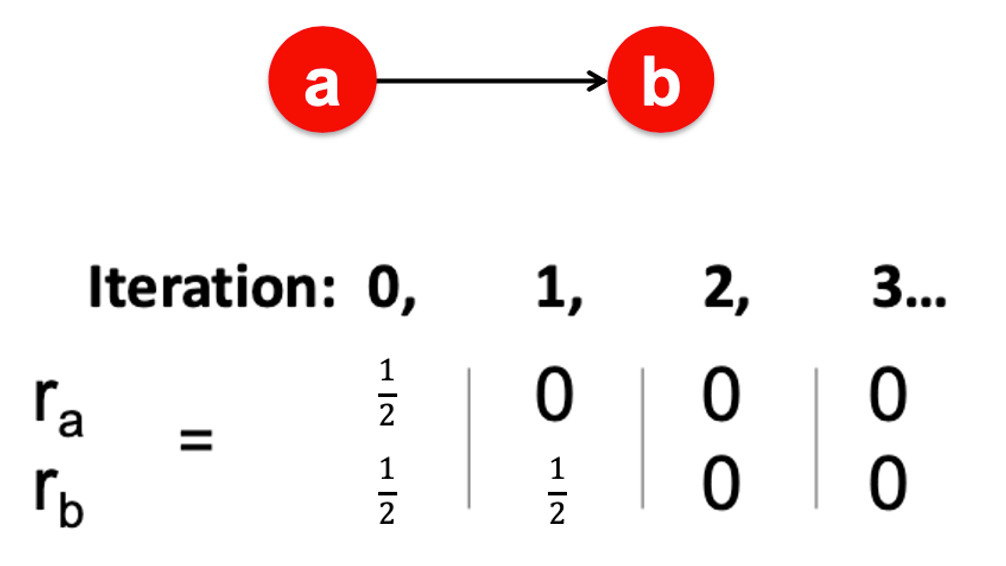
• (e.g.) dead end 문제가 발생하는 경우 (그림 7)
  • 모든 node의 rank가 모두 0으로 수렴합니다.

• 해결 방법은 밑에서 알아보도록 하겠습니다.

---

• 논문에서는 dead end를 모두 제거한 후에, rank를 계산했습니다.
• 논문의 2.7 Dangling Links을 보면, 다음과 같이 나와있습니다.

dangling links는 다른 페이지의 rank에 직접적인 영향을 미치지 않기 때문에, 모든 PageRank가 계산될 때까지 시스템에서 dangling links를 제거하기만 하면 됩니다.

제거된 dangling links와 같은 페이지에 있는 다른 edge의 normalization은 약간 변하지만, 큰 영향은 없을 것입니다.

---

5 Simple PageRank

5.1 Spider trap과 Dead end의 해결 방법

• spider trap과 dead end 문제를 해결하는 방법은 teleport (순간 이동, 점프) 입니다.

• random walk 관점에서, 웹을 서핑하는 웹 서퍼의 행동을 다음과 같이 수정합니다.
  1. 현재 웹 페이지에 하이퍼링크가 없다면, 랜덤한 웹 페이지로 teleport 합니다.
  2. 현재 웹 페이지에 하이퍼링크가 있다면,
     • $\alpha$의 확률로, 하이퍼링크 중 하나를 uniform한 확률로 선택해 이동합니다.
     • $(1 - \alpha)$의 확률로, 랜덤한 웹 페이지로 teleport 합니다.

• teleport를 하는 경우엔, teleport 할 random한 웹 페이지는 전체 웹 페이지들 중에 하나를 uniform한 확률로 선택합니다.
• teleport에 의해서, spider trap이나 dead end에 갇히는 일이 없어집니다.
• $\alpha$를 damping factor라고 부르며, $[0.8,\; 0.9]$ 정도를 사용합니다.

---

• teleport를 도입함으로써, rank의 계산 식은 아래와 같이 바뀌게 됩니다.

• simple PageRank의 식

\[r_j = \sum_{i \rightarrow j}^{} \frac{r_i}{d_i}\]

• simple PageRank의 식
  • $N$은 총 웹 페이지 (node)의 수를 의미합니다.
  \[\displaystyle r_j = \sum_{i \rightarrow j}^{} \bigg( \alpha \frac{r_i}{d_i} \bigg) + (1-\alpha) \frac{1}{N}\]
  • 식 $\displaystyle \sum_{i \rightarrow j}^{} \bigg( \alpha \frac{r_i}{d_i} \bigg)$ 는 하이퍼링크를 따라 node $j$에 도착할 확률을 의미합니다.
  • 식 $\displaystyle (1-\alpha) \frac{1}{N}$ 은 teleport를 통해 node $j$에 도착할 확률을 의미합니다.

4.2 Simple PageRank 계산 예시

• 그림 8과 같은 웹 그래프가 있을 때, PageRank를 계산하는 방법에 대해 알아보겠습니다.

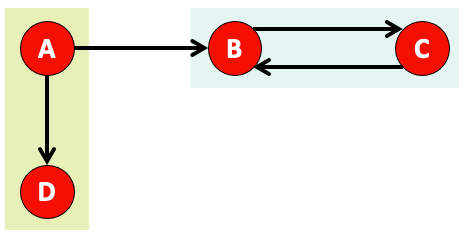
1. adjacency matrix $A$ 구하기

• 웹 그래프의 adjacency matrix $A$ 를 구합니다.
• $A$는 row node에서 column node로 가는 edge가 있으면 1, 없으면 0 입니다.

• (e.g.)

\[A = \begin{bmatrix} 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix}\]

2. $A$를 transpose한 matrix $A^T$ 구하기

• adjacency matrix $A$를 transpose한 matrix $A^T$ 구합니다.
• $A^T$는 column node에서 row node로 가는 edge가 있으면 1, 없으면 0 입니다.

• (e.g.)

\[A^T = \begin{bmatrix} 0 & 0 & 0 & \color{red}{0} \\ 1 & 0 & 1 & \color{red}{0} \\ 0 & 1 & 0 & \color{red}{0} \\ 1 & 0 & 0 & \color{red}{0} \\ \end{bmatrix}\]

3. hyperlink matrix $H$ 구하기

• adjacency matrix인 $A$를 hyperlink matrix $H$로 변환합니다.
• $A$의 값들을, column별로, column의 합으로 나눕니다.

• (e.g.)

\[H = \begin{bmatrix} 0 & 0 & 0 & \color{red}{0} \\ \frac{1}{2} & 0 & 1 & \color{red}{0} \\ 0 & 1 & 0 & \color{red}{0} \\ \frac{1}{2} & 0 & 0 & \color{red}{0} \end{bmatrix}\]

4. column stochastic matrix인 $M$ 구하기

• PageRank의 수렴을 보장하기 위해 column stochastic matrix가 필요합니다.
  • 따라서, hyperlink matrix $H$를 column stochastic matrix인 $M$으로 만듭니다.
• column stochastic matrix는
  • matrix의 모든 값들이 음수가 아니여야 합니다.
  • 각 column의 합이 1입니다.
• column stochastic matrix를 만들어줌으로, dead end 문제가 해결됩니다.

• (e.g.)

\[M = \begin{bmatrix} 0 & 0 & 0 & \color{red}{\frac{1}{4}} \\ \frac{1}{2} & 0 & 1 & \color{red}{\frac{1}{4}} \\ 0 & 1 & 0 & \color{red}{\frac{1}{4}} \\ \frac{1}{2} & 0 & 0 & \color{red}{\frac{1}{4}} \end{bmatrix}\]

5. Google matrix $G$ 구하기

• column stochastic matrix인 $M$을 이용하여, PageRank를 구하는 Google matrix $G$ 구합니다.
• spider trap 문제는 랜덤 서퍼 개념을 도입함으로써 해결됩니다.
• $\alpha$는 보통 $[0.8,\; 0.9]$ 정도를 사용합니다.

• (e.g.)

\[G = \alpha \begin{bmatrix} 0 & 0 & 0 & {\frac{1}{4}} \\ \frac{1}{2} & 0 & 1 & {\frac{1}{4}} \\ 0 & 1 & 0 & {\frac{1}{4}} \\ \frac{1}{2} & 0 & 0 & {\frac{1}{4}} \end{bmatrix} + (1-\alpha) \begin{bmatrix} \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} \\ \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} \\ \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} \\ \frac{1}{4} & \frac{1}{4} & \frac{1}{4} & \frac{1}{4} \end{bmatrix}\]

• $\alpha = 0.8$이라고 하면, $G$는 다음과 같습니다.

\[G = \begin{bmatrix} 0.05 & 0.05 & 0.05 & 0.25 \\ 0.45 & 0.05 & 0.85 & 0.25 \\ 0.05 & 0.85 & 0.05 & 0.25 \\ 0.45 & 0.05 & 0.05 & 0.25 \end{bmatrix}\]

5. rank 벡터 $r$ 구하기

• rank 벡터와 Google matrix $G$ 를 곱하여, rank를 구합니다.
• power iteration을 이용하여, 다음 식을 풀어, 최종 rank 벡터를 구합니다.

\[r = G \cdot r\]

• (e.g.)

\[r \approx \begin{bmatrix} 0.07 \\ 0.42 \\ 0.41 \\ 0.10 \end{bmatrix}\]

---

6 PageRank의 결과

6.1 Convergence Properties

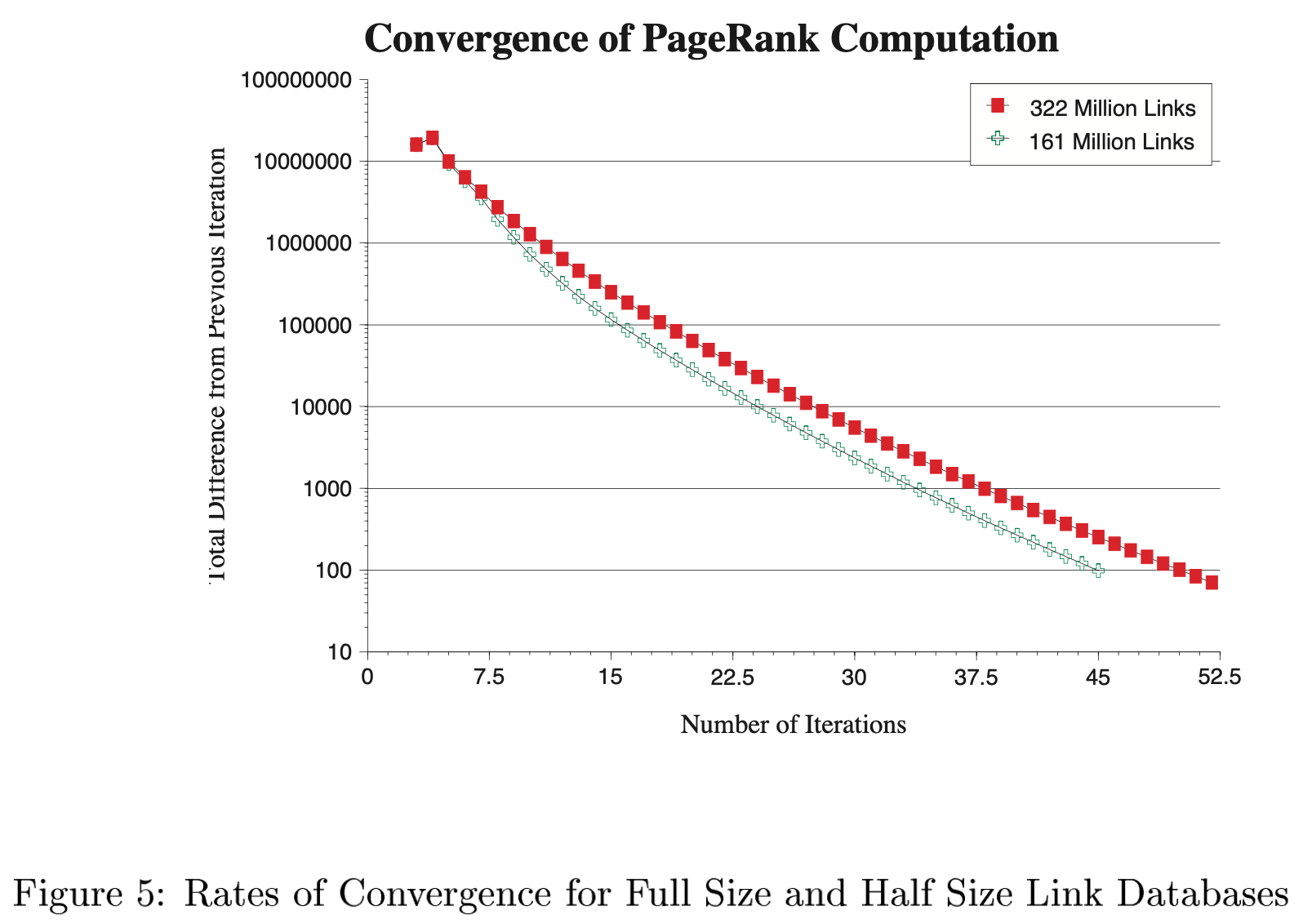
• 그림 9
  • 3억 2200만 개의 edge → 52번의 iteration을 통해 수렴
  • 1억 6100만 개의 edge → 45번의 iteration을 통해 수렴
• PageRank가 매우 큰 데이터에서도 매우 잘 확장될 것임을 시사합니다.

---

7 질문

7.1 구글은 지금도 PageRank를 사용할까?

• PageRank 논문은 1998년에 나왔지만, 구글은 현재도 검색 엔진의 품질 향상을 위해 PageRank를 사용하는 것으로 알려져 있습니다.

Sumin.Han's profile image

Sumin.Han

2022-03-25 13:03

Read more posts by this author