ㅤ안녕하세요, 가짜연구소 Groovy Graph 팀의 최선웅입니다. 이 글은, ‘Inductive Representation Learning on Large Graphs’ 논문을 읽고, 정리한 글 입니다.
ㅤ이 글은 Reference 자료들을 참고하여 정리하였음을 먼저 밝힙니다. 혹시 내용중 잘못된 점이나 보완할 점 있다면 댓글로 알려주시면 감사하겠습니다. 그럼 시작하겠습니다.
목차
0. Abstract
- Large graphs에서 node embedding은 다양한 prediction 문제에 매우 유용하게 사용됩니다.
- 하지만 기존의 방법들의 embedding을 학습하는 과정에서 모든 node가 필요하다는 문제점을 가지고 있습니다.
- 기존의 방법들은 Transductive하고, 보지 못한 node에 대해 일반화를 하지 못합니다.
- GraphSAGE는 Inductive한 방법이기 때문에 이러한 문제를 해결할 수 있습니다.
- Embedding을 만드는 function을 학습하는 방식으로 진행됩니다.
- 여러 데이터셋에 SOTA 성능을 달성했습니다.
1. Introduction
- Node embedding의 기본적인 아이디어는 Dimensionality Reduction 입니다. 즉 고차원의 정보를 저차원의 dense vector embedding으로 변환시키는 것입니다.
- 이전의 연구들은 고정된 그래프에 대한 embedding을 다루는데, 이는 그래프의 사이즈가 계속해서 변하는(dynamic) 현실에 적용하기 적합하지 않습니다.
- 따라서 계속해서 변하고 새로운 노드들을 다루는 상황에서는 inductive한 방식이 필요하게 됩니다.
- 하지만 inductive한 방식에는 어려운 측면이 존재합니다.
- unseen nodes에 대한 일반화는 새로 관측된 subgraph를 기존에 알고리즘이 최적화된 embedding에 맞게 “aligning” 하는 과정이 필요하기 때문입니다.
- Graph A에 최적화 된 알고리즘을 새로 관측된 subgraph B에 맞춰야 한다는 점이 어렵다고 이해했습니다.
- 기존의 방식들은 대부분 transductive 하기 때문에 inductive하게 수정할 경우 많은 계산비용이 듭니다.
- GCN 방법 또한 고정된 그래프에서의 transductive한 경우에서만 적용가능한 문제가 있습니다.
Present work
- GraphSAGE(SAmple and aggreGatE)는 node feature를 활용해서 unseen nodes에 대한 일반화 문제를 해결하려고 합니다.
- 학습 알고리즘에서 node features들을 통합하면서 node의 이웃들에 대한 topological structure와 이웃에 속한 node feature들의 distribution에 대해서도 학습합니다.
- 각 node에 대해 embedding vector를 학습하기 보다는, 주변 이웃(local neighborhood)를 이용한 aggregator functions의 집합을 학습합니다.
- 따라서 예측 단계에서도 학습한 aggregator functions를 이용해 embedding을 만들어냅니다.
- 실제 다양한 citation, Reddit, protein-protein interactions 데이터에 대해 좋은 결과를 보입니다.
2. Related work
기존 GNN에서 사용하던 다양한 embedding 방법들에 대해 알아보겠습니다.
Factorization-based embedding approaches
- Random walk와 MF(Matrix Factorization)-based learning objective를 통해 저차원 node embeddings를 학습합니다.
- 이러한 방법에는 Spectral clustering, multi-dimensional scaling, PageRank등이 있다.
- 각 노드들에 대한 embedding을 학습한다. 따라서 transductive하고 추가적인 학습이 필요합니다.
- Objective ft이 orthogonal transformation에 대해 invariant하기 때문에, embedding space가 일반화 되기 어렵고 re-training과정에서 drift할 수 있다.
- Planetoid I 라는 방법이 존재하나 그래프 구조를 regularization으로 활용한다. (이 부분은 추가적으로 이해가 되는대로 내용을 보충하겠습니다.)
Supervised learning over graphs.
- Node embedding 방법 이외에도 다양한 supervised learning 방법이 존재합니다. Graph kernel을 사용해 graph의 feature vector를 구하는 다양한 kernel-based 방법이 존재합니다.
Graph convolutional networks
- Convolutional neural networks를 통해 학습시키는 여러개의 방법이 제안됐는데, 이러한 방법들의 대다수는 큰 그래프로 scaling되지 않고, 전체 그래프 분류를 목적으로 하고 있습니다.
- GraphSAGE 방법은 GCN과 높은 관련성이 있습니다. 하지만 GCN은 transductive한 상황에서 semi-supervised learning 방법으로 만들어져있고, 학습과정에서 graph Laplacian을 알고 있어야한다는 문제가 있습니다.
3. Propsed method: GraphSAGE
GraphSAGE에서 제안한 방법들을 본격적으로 살펴보겠습니다.
3.1 Embedding generation algorithm
우선 알고리즘 형태로 간단하게 살펴보겠습니다.
 간단하게 그림으로 표현하면 아래와 같습니다.
간단하게 그림으로 표현하면 아래와 같습니다.
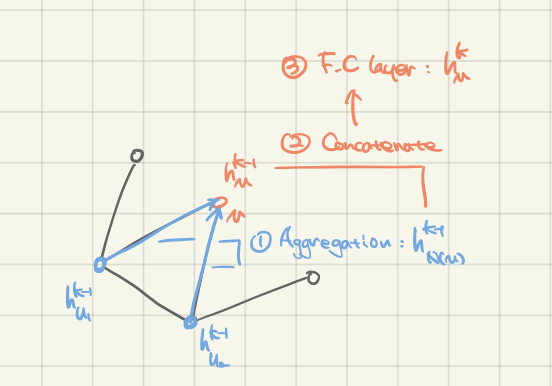
- Node의 이웃들로부터 정보를 aggregate 한다.
- Aggregate된 정보를 원래의 representation $h^{k-1}_{v}$와 concatenate 한다.
- 2를 non-linear activation을 사용한 fully connected layer로 보낸다.
- 3의 결과를 normalization 한다.
→ 이 과정 K번 거쳐 최종적으로 나오는 representation을 $z_{v} = h^{K}_v$로 notate한다.
Releation to the Weisfeiler-Lehman Isomorphism Test.
- 다음의 조건들을 가정하면 Algorithm1이 WL test, “naive vertex refinement”의 한 예가 될 수 있습니다. 즉, 두 그래프의 최종 representation이 똑같은 경우, 두 그래프가 isomorphic하다고 할 수 있다는 의미가 된다고 합니다.
- 상세 내용은 아래와 같습니다.
-
$K = V $ - $W = I, \text{ Identity matrix.}$
- No-non-linear hash function as an aggregator
-
Neighborhood definition
-
GraphSAGE에서는 Computational footprint를 위해 고정된 크기의 이웃 집합을 사용합니다. (계산량을 체크할 수 있다는 의미 같습니다.) 이러한 과정 없이는 최악의 경우 계산량이 $O( \mathcal{V} )$가 될 수 있습니다.
3.2 Learning the parameters of GraphSAGE
- Fully unsupervised한 학습을 하기 위해 최종 representation $\mathbf{z}_u$에 graph-based loss function을 적용합니다.
- Weight matrices $\mathbf{W}^k$와 aggregator function의 parameter를 stochastic gradient descent를 통해 조정합니다.
→ Positive sample은 random walk를 통해서 계산, negative sample은 랜덤(분포)하게 계산합니다.
- $v$: $u$ 근처에서 fixed-length random walk를 했을 때 공통적으로 나타나는 노드.
- $\sigma$: sigmoid function
- $P_n$: negative sampling distribution
- $Q$: negative sample의 갯수
3.3 Aggregator Architectures
그래프 구조에 순서가 있지 않기 때문에 순서에 영향이 없는 aggregator가 필요하게 됩니다.
Mean aggregator
\[h^k_v \leftarrow \sigma(\mathbf{W}\cdot\text{MEAN}(\{\mathbf{h}^{k-1}_v\} \cup \{\mathbf{h}^{k-1}_u, \forall u \in \mathcal{N}(v)\})).\]- Localized spectral convolution의 rough한 linear approx.이기 때문에 convolutional 이라고 부릅니다.
- 이 aggregator를 사용할 때는 별도의 concatenation을 진행하지 않는데, 이는 일종의 skip connection으로 볼 수 있기 때문입니다.
LSTM aggregator
- LSTM 구조를 통해 표현력을 높일 수 있습니다.
- LSTM 에서도 순서를 상관하지 않기 위해 random하게 permutation을 통해 계산합니다.
Pooling aggregator
\[\text{AGGREGATE}^{\text{pool}}_k = \max(\{\sigma(\mathbf{W}_{\text{pool}}\mathbf{h}^{k}_{u_i}+b), \forall u_i \in \mathcal{N}(v)\})\]4. Experiment
-
3가지 benchmart tasks에 대해 실험을 진행했습니다.
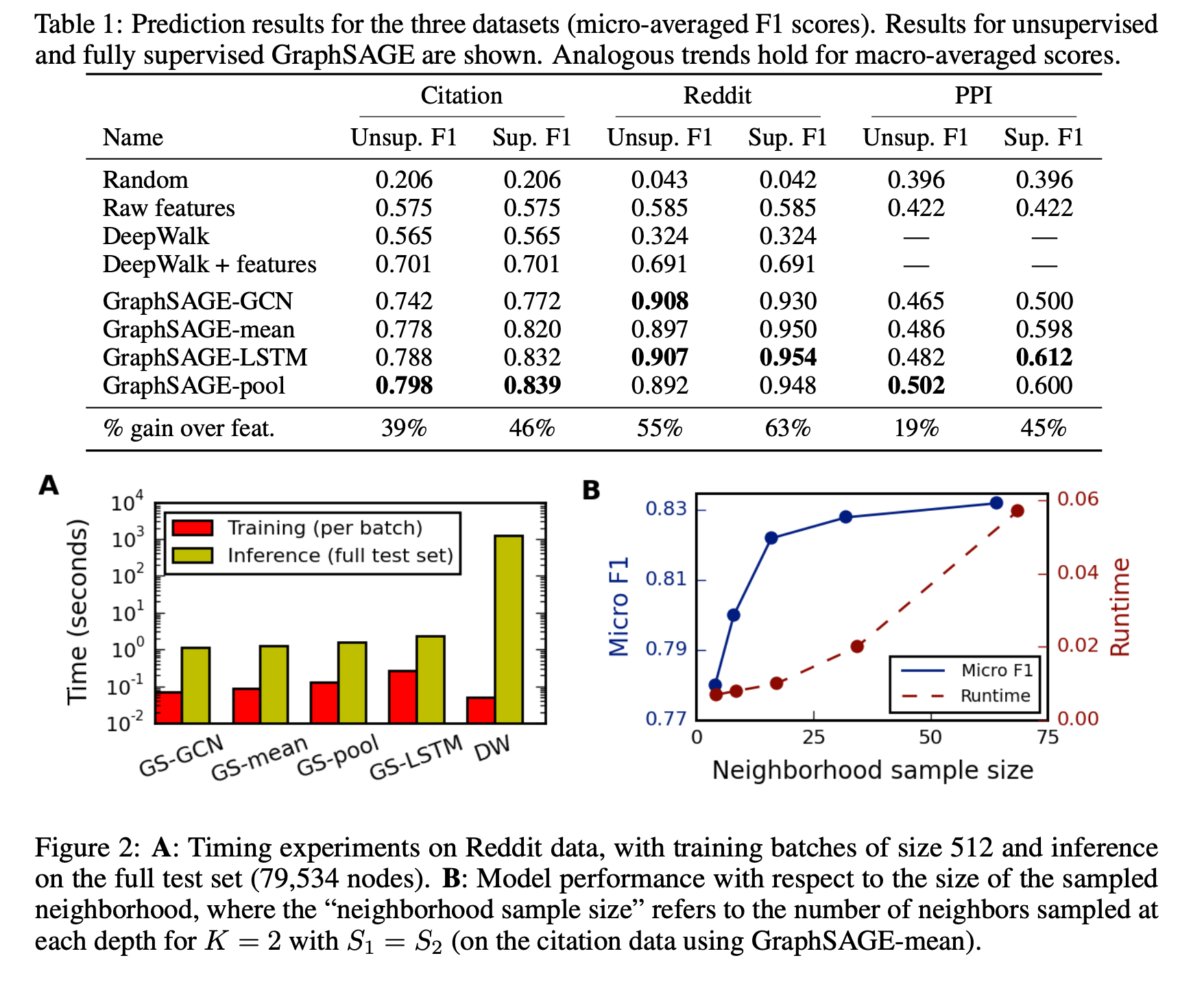
- GraphSAGE가 다른 방법보다 더 좋은 성능을 보입니다.
- 속도측면에서도 효과적이며, 이웃의 수가 증가함에 따라 속도와 성능 둘다 증가합니다.
5. Therotical analysis
- 조금 더 보완 후 내용을 추가하겠습니다.
6. Conclusion
- unseen node의 임베딩을 효과적으로 만드는 inductive한 방법을 제안했습니다.
- 3개의 데이터셋에 대해 SOTA 성능을 보입니다.
- 하지만 성능과 샘플 수에 따른 trade-off가 존재합니다.
- 추후에는 non-uniform하게 샘플링하는 방법을 제안할 예정.