Exploiting Edge Features in Graph Neural Networks

안녕하세요, 가짜연구소 Groovy Graph 팀의 서호준입니다. 이번 포스트에서는 2018년도에 소개 된 Exploiting Edge Features in Graph Neural Networks 논문에 대해 리뷰해 보도록 하겠습니다.

0. Abstract

많은 사람들이 현재 활발히 사용하고 있는 GCNs와 GAT모델은 edge feature 활용성 면에 대해 제한적인 측면이 있다.
그렇기 때문에 edge feature를 undirected or multi-dimensional edges 측면에서도 더욱 충분히 사용할 수 있는 새로운 프레임워크를 고안해 내었다.
현재 주 모델들에서 사용되고 있는 symmetric normalization 방법이 아닌 doubly stochastic normalization 방법을 제안하였다.
각 레이어에서 새로운 formula를 생성해 내어 multi dimensional edge feature를 사용 할 수 있도록 한다.
Edge features가 네트워크 레이어 전반적으로 고루 사용될 수 있다.

1. Introduction

현재 대표적인 GNN 모델로 GCNs와 GAT 등이 많이 사용되고 있다.
GCNs와 GAT의 본질은 확연히 다르다 → GCNs에서 이웃 노드를 취합하는 것은 Graph Topological Structure에 의해 정의되는 반면 (Node feature와는 무관하게), GAT의 weights는 어텐션 메카니즘에 의해 node feature의 함수로 정의된다. GCNs에서는 오직 one-dimensional real value edge feature를 사용하기 때문에 이 역시 edge information은 그저 edge가 존재 하느냐 마느냐 인 것이기 때문에 edge feature를 제대로 사용하고 발휘하고 있다고 볼 수 없다.
GAT과 GCN의 레이어는 node feature를 original adjacency matrix를 인풋으로 사용하는데, 이는 noisy하거나 not optimal할 수 있기 때문에 효과가 제한적일 수 있다고 한다.

옛날에 graph learning에서 그래프 데이터의 복잡한 non-Euclidean structure를 해결하기 위해

Graph-statistics (e.g., degrees)를 추출하거나
Kernel functions을 사용하거나
Hand-crafted features를 고안하였다.

이후에는 data driven embedding approach를 사용하게 되었다.

대표적인 embedding approach들의 한계점은

Low-dimensional vectors를 맵핑하는 function이 linear하거나 너무 간단한 function을 사용하여 복잡한 패턴을 풀어내지 못하였다.
DeepWalk, Node2Vec 등 대부분은 node features를 모델에서 사용하지 않는 문제가 있었다.
이러한 모델들은 모두 transductive한 문제가 있었다.

이러한 문제점을 풀기위해 이후에는 neural networks가 graph learning에서 사용되기 시작하였다. GCNs와 GAT이 대표적인 예이다.

3. Edge feature enhanced graph neural networks

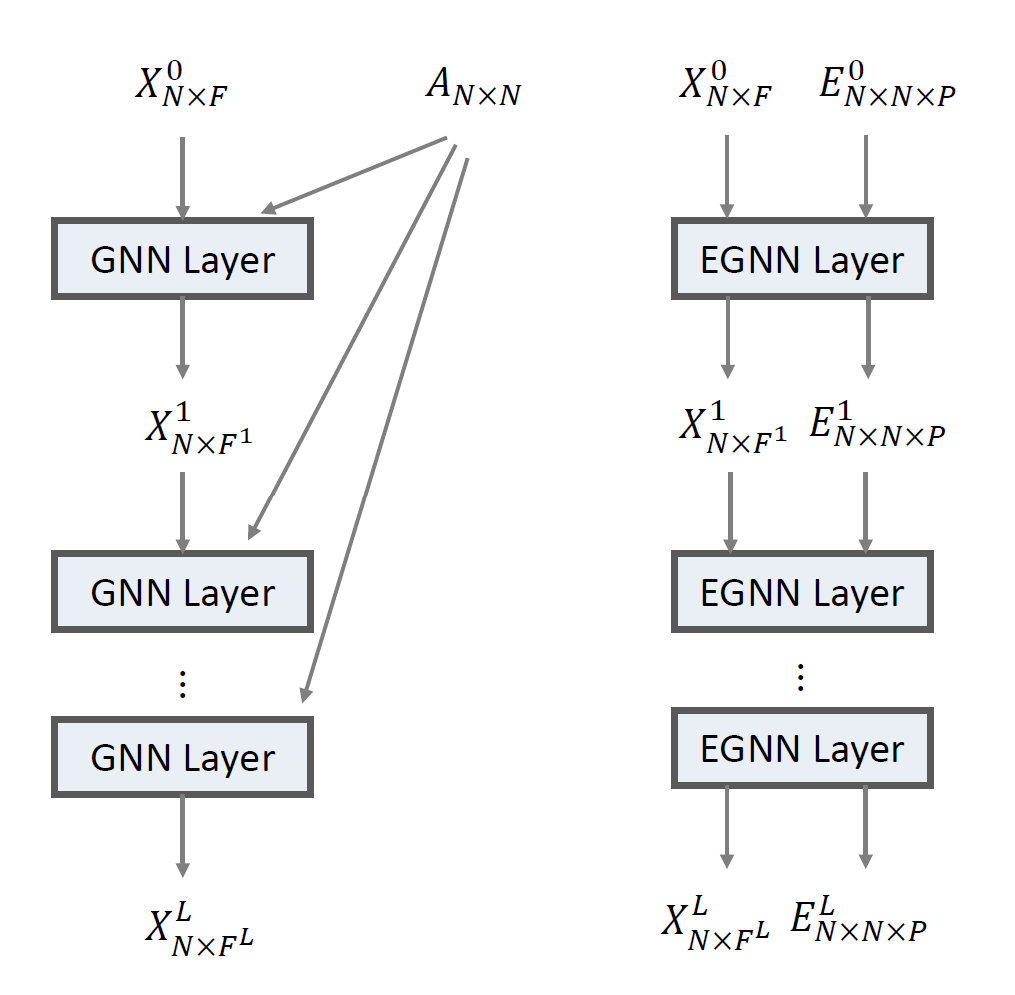
3.1. Architecture overview

N개의 nodes가 있을 때, node feature를 X라고 한다면 X는 NxF matrix representation이 된다고 정의한다.
· 은 whole range of a dimension을 슬라이스 하는 것을 말한다.
즉, X$_i$,$_j$는 X$i$의 $j$번째 feature를 말하는 것이다.
X$_i$· ∈ R$^F$ 는 $i$번째 노드의 F dimensional feature를 말하는 것이다.
E는 NxNxP 형태의 텐서로서 edge feature를 나타낸다.
E$_i$,$_j$· ∈ R$^P$ 는 P dimensional feature를 가지고 있고 node $i$에서 node $j$로 이어지는 edge를 말하는 것이다.
E$_i$,$_j$· = 0 인 경우는 $i$와 $j$사이에 edge가 존재하지 않는다고 정의한다.
$l$을 superscript로 사용하여 lth 레이어임을 표시해 준다.
Input은 X$^0$와 E$^0$로 나타낸다.
첫 EGAT레이어를 거치고 나면, X$^0$는 NxF$^1$의 value를 생성해 내고 이는 X$^1$이다.
그 와중에 E$^1$은 E$^0$의 dimension을 모두 preserving 하며 만들어지고, 이 E$^1$는 그 다음 레이어의 edge feature로 사용된다.
The node features X$^l$은 F$^l$ 차원공간에서의 노드 엠베딩이다.
노드 분류 문제에서는 각 노드 엠베딩 값 X$^l$,$_i$의 last dimension 값을 softmax를 통과시켜 아웃풋을 얻어낸다.
그래프 prediction 문제(Regression and classification)는 pooling layer가 first dimension에 적용되어 feature matrix가 전체 그래프를 나타내는 single vector embedding로 만들고, 그 후에 fully connected layer를 적용하여 아웃풋을 만들어 이 아웃풋으로 regression을 하던 classification을 진행하던 한다.
E$^0$는 pre-normalized되어 있다는 것을 참고하자. (Pre-normalization에 대해서는 뒤에 얘기)
이 논문에서는 EGNN을 EGNN(A), EGNN(C)로 두가지를 제안하여 GAT과 GCNs과 비교한다.

3.2 Doubly stochahstic normalization of edges

                                               Doubly Stochastic Matrix  <img src="/graph/files/posts/Exploiting-Edge-Features-for-Graph-Neural-Networks/Doubly_stochastic.png" width="500px"> 일반적으로 Markov Transition Matrix가 행과 열 모든 곳에서 1.0으로 총합을 이루는 것 Matrix를 Doubly Stochastic Matrix라고 한다.

Doubly Stochastic Normalization

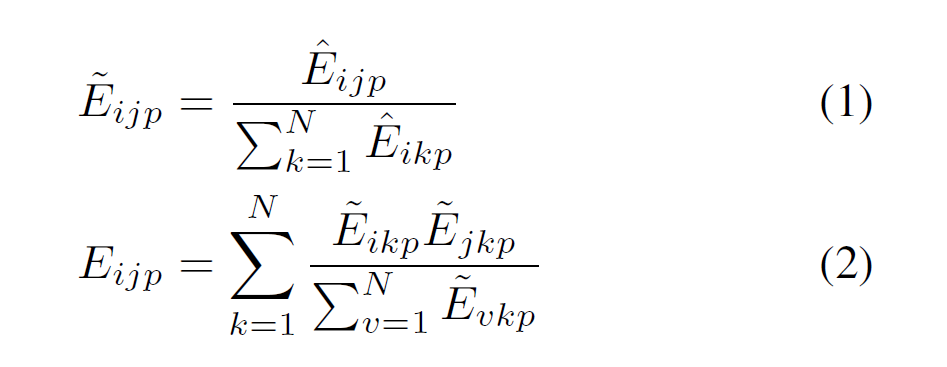E~$_i$,$_j$,$_p$는 일반적인 E$_i$,$_j$,$_p$를 softmax로 normalizing하는 것이지만 이 논문에서는 이렇게 한번 정규화 시킨 후 다시 한번 더 루프를 돌면서 정규화를 해준다.

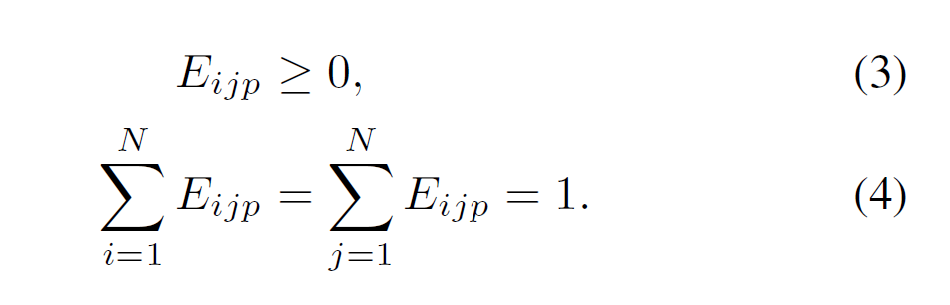즉, source node 측면에서도 합은 1, destination node 측면에서도 합은 1이 되어 doubly stochastic matrix가 된다.

그렇기 때문에 수학적으로,

a stationary finite Markov chain with a doubly stochastic transition matrix will have a uniform stationary distribution 하다

*Stationary Markov Chain은 Mp = M이 되는 matrix이다.

Graph neural networks에서는 edge features가 레이어를 지남에 따라 반복적으로 곱해지는데, 이때 doubly stochastic normalization이 이 프로세스를 안정화 시킬 수 있다고 한다.

B. Wang, A. Pourshafeie, M. Zitnik, J. Zhu, C. D. Bustamante, S. Batzoglou, and J. Leskovec. Network Enhancement: a general method to denoise weighted biological networks.

Doubly Stochastic Matrix의 효과는 위의 논문에서 graph edge denoising측면에서 이미 입증되었다고 한다.

3.3. EGNN(A): Attention based EGNN layer

GAT의 경우 edge feature는 그저 이웃노드들이 있는지 없는지의 binary value를 가지고 있을 뿐이다. 즉, weights같은 real value feature는 고려하지 않는다.
이 논문에서는 다양한 edge feature를 같이 사용하는 새로운 어텐션 메카니즘을 제안한다. EGNN(A) layer formula 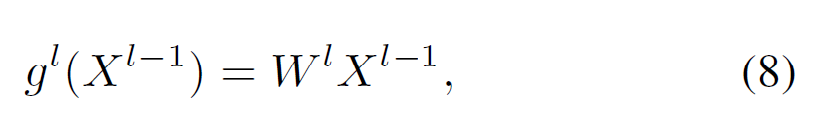g$^l$-transformation formula
g$^l$-transformation은 단순히 이전 레이어의 node embedding을 weight matrix W$%l$$^l$에 행렬곱을 해 주는 operation이다.

요약: g-transformation된 node feature와, p-edge feature와 node feature를 α-transformtion한 값을 곱한 것을 P채널로 concatenation(?)한 값을 non-linear activation을 통과시켜 준다. 그렇게 함으로써 그 다음번 레이어의 node embedding을 구하는데 사용한다.

α$_i^l$,$_j$,$_p$값은 $X_i^l$ $^-$ $^1$, X$_j^l$ $^-$ $^1$의 함수이며 α는 우리가 말하는 attention coefficients이다.

일반적으로 attention mechanism의 attention coefficients는 X$i$,$.$와 X$j$,$.$두 nodes에만 의존하여 계산되지만, 이 논문에서는 그 두 nodes외에 edge features에도 의존하여 계산될 수 있게 하였다.
Multi dimensional edge feautures를 위해서 각 feature channel마다 위 공식으로 계산을 한 후 concatenation을 통해 병합하여 계산한다.

특정 edge feature channel을 위해 이 논문의 attention function을 요약해보면 다음과 같다.

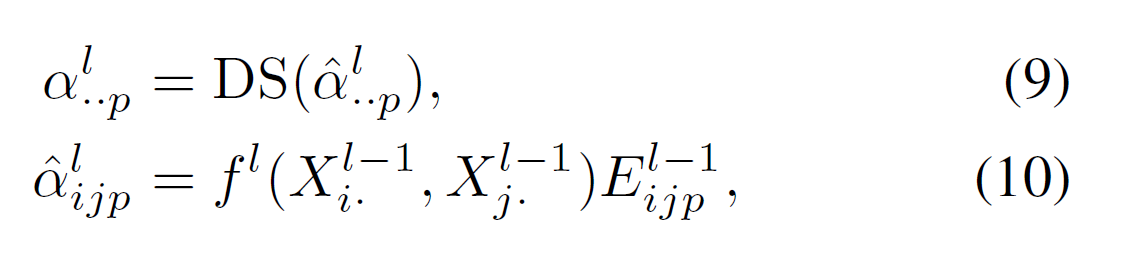
DS: Doubly Stochastic Normalization

f$^l$: Scalar value로 아웃풋을 나타내는 아무 attention function을 말한다.

이 논문에서는 아래 공식 (11)과 같이 linear function을 사용하였다고 한다.

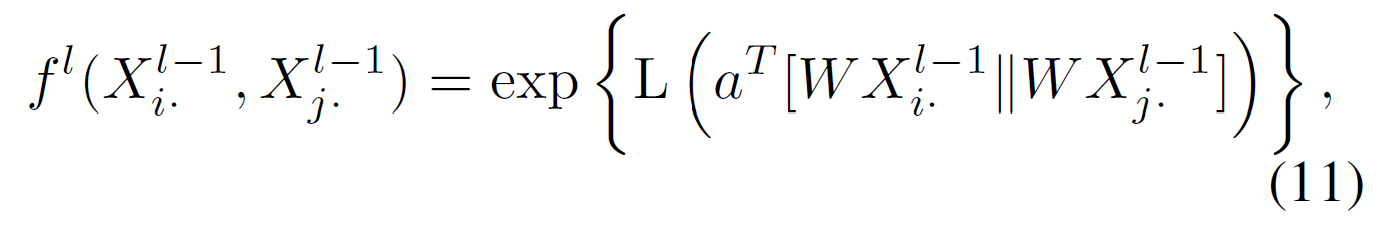아래 공식 (12)에서 볼 수 있듯이 attention coefficients가 다음 레이어에서 edge features로 사용된다고 한다.

3.4 EGNN(C): Convultion based EGNN layer

EGNN(C)와 EGNN(A)의 차이는 attention coefficients를 사용하는가 adjacency matrix를 사용하는지이다. 그러므로 이 논문에서 α..$_p$대신 E..$_p$를 사용하는 차이가 있다.

3.5. Edge features for directed graph

이 논문에서는 edges의 방향성이 representation expressiveness에 중요하기 때문에 direction을 잃지 않는 것이 중요하다고 하였다. 그래서 directed E$_i$,$_j$,$_p$가 아래와 같이 표현되도록 하였다.

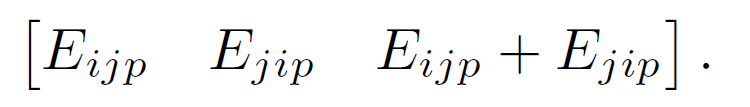
이렇게 모든 directed channel들은 3개의 channels로 증강된다. 이렇게 증강된 3개의 채널은 3타입의 이웃을 정의한다 (Forward, Backward and Undirected).

4. Experimental results

4.1. Citation networks

텐서플로우 sparse tensor functionality를 사용하여 아주 효율적으로 메모리를 줄이고 복잡한 계산을 할 수 있었다고 한다 (On Nvidia Tesla K40 with 12G graphics memory)
Cora, Citeseer 그리고 Pubmed 데이터 셋을 사용하였다.
일반적으로 이 데이터들은 edge direction을 버리는 pre-processing을 거친 것이기 때문에 오리지널 데이터를 가져와서 edge direction을 참고했다.
Activation Function으로 ELU를 사용했다.
20번씩 모든 버전의 알고리즘을 돌려봤다. 그 후 classification accuracies의 mean과 standard deviation기록하였다.
데이터들의 Class distribution이 다 imbalanced하기 때문에 이를 테스트 하기 위해 unweighted와 weighted losses를 둘 다 테스트해서 퍼포먼스를 보았다. Class k에 속하는 노드의 weight를 계산하기 위해 아래 공식이 사용 되었다.

K: class의 갯수

n$_k$: Training se 에서 k-class에 속하는 nodes.

즉, 숫자가 적은 소수 클래스에 있는 nodes는 더 큰 weights를 가지고 그에 따라 loss계산 시 더 penalized된다.

성능 결과는 아래와 같다.

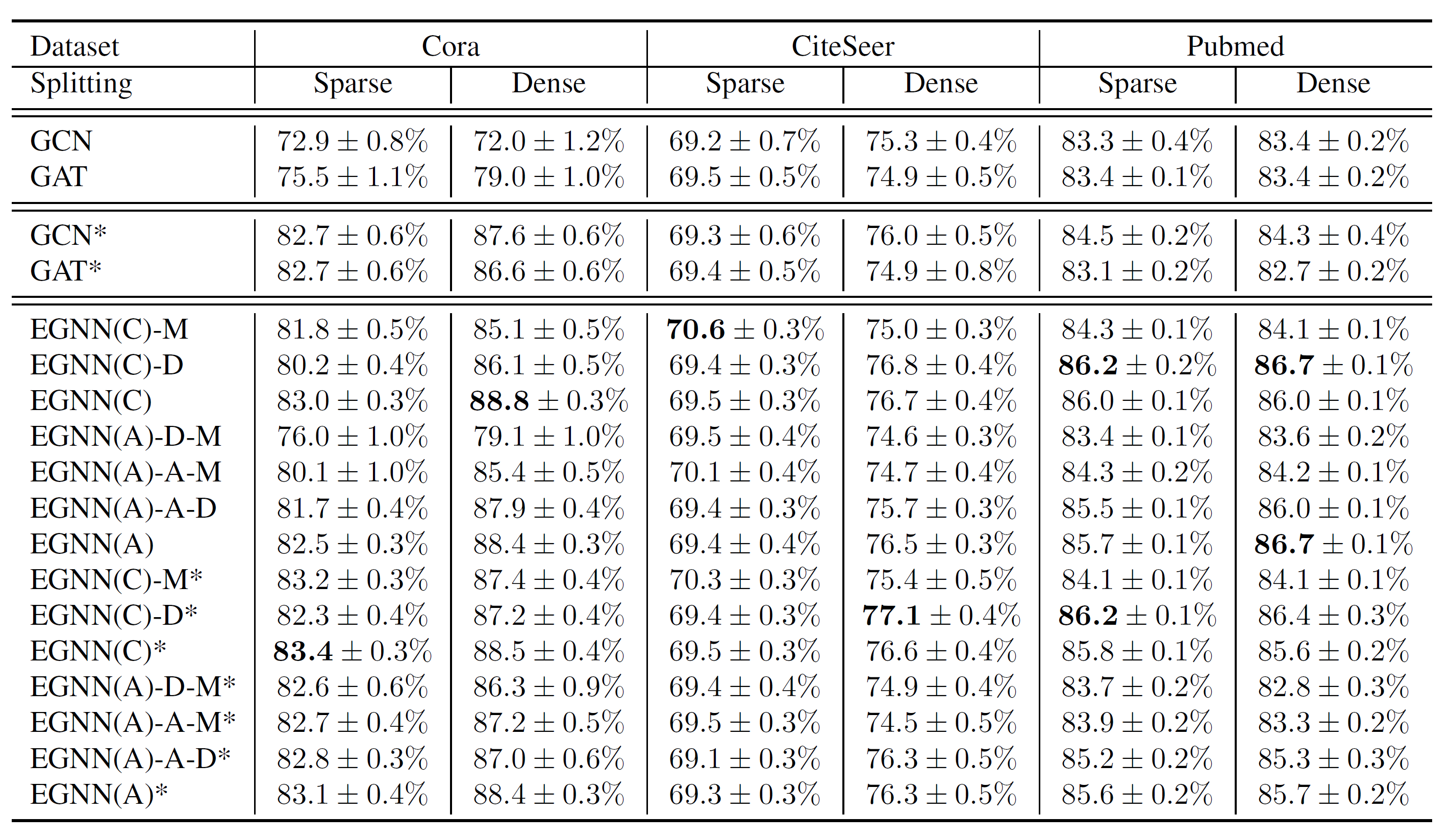
EGNN(C)-M* or EGNN(C)-D*은 GCN이랑 비슷하거나 조금 더 나쁜 성능을 보여준다. 그러나 EGNN(C)는 훨씬 좋은 성능을 보인다. Multi-dimensional edeg features와 doubly stochastic normalization이 같이 사용되었을 때 확연히 좋은 성능을 보이는 것이 감지되었다.

4.2. Molecular analysis

분자 구조 분석 태스크에서는 Whole graph prediction을 하게 되는 경우가 대부분이다.
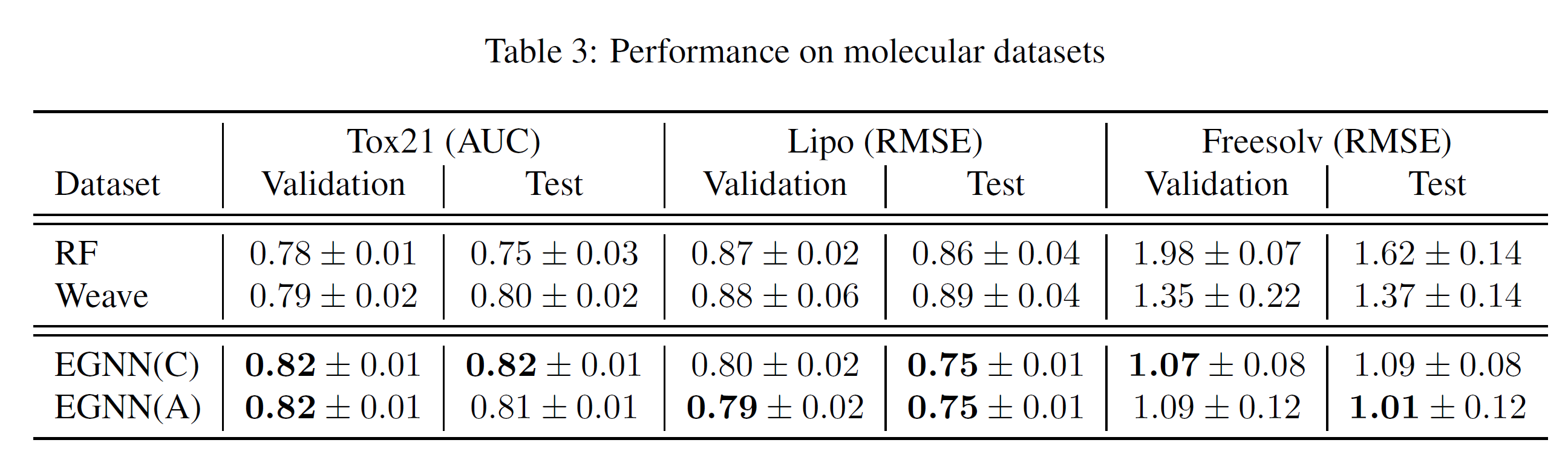
데이터는 Tox21(multi-label classification problem) , Lipo 그리고 Freesolv(regression tasks)를 사용하였다.
이 실험에서 2 graph processing layers를 사용하였고, a gloabal max-pooling layer와 a fully connected layer를 사용하였다고 한다.

성능 결과는 아래와 같다.

5. Conclusions

그래프 인공 신경망에서 현존하는 문제점들을 풀어내기 위한 새로운 프레임워크를 제안하였다.
Multi-dimensional edge features를 활용하였다.
Doubly Stochastic Normalization을 사용하였다.

Back to Posts

Exploiting Edge Features in Graph Neural Networks

목차

0. Abstract

1. Introduction