안녕하세요, 가짜연구소 Groovy Graph 팀의 김은희입니다😀. 첫 포스팅으로는 NeurIPS 2013에 소개된 Distributed Representations of Words and Phrases and their Compositionality 를 리뷰하도록 하겠습니다.

Goal
1. 기존 Skip-gram의 문제
2. 기존 Skip-gram의 보완 방법
첫번째 아이디어 : Phrase 기반 학습
두번째 아이디어 : Negative sampling(NEG) 사용
1. 기존 Skip-gram의 objective function
2. 기존 Skip-gram의 hierarchical softmax
3. Negative sampling의 도입
세번째 아이디어 : Subsampling 사용
References

Goal

Skip-gram의 vector representation quality를 높이자!

Skip-gram 은 ① 단어 기반으로 학습을 진행하고 ② Objective function 안에 softmax function을 사용하며 ③ 말뭉치(corpus) 안에 드물게 등장하는 단어와 빈번하게 등장하는 단어 간의 불균형이 존재하는 특징이 있습니다.

기존 Skip-gram의 문제

이러한 특징들은 크게 세 가지의 문제를 발생시킵니다.

관용구들을 잘 represent하지 못합니다.

예를 들어 ‘Air’와 ‘Canada’는 각 단어의 의미상 연관성이 존재하지 않습니다. 하지만 ‘Air Canada’는 항공사 ‘Air Canada’라는 의미를 가지고 있습니다. 단어 기반으로 학습을 진행하는 Skip-gram은 이와 같은 관용구를 잘 represent하지 못합니다.

많은 연산량을 요구합니다.
빈번하게 등장하는 단어가 항상 드물게 등장하는 단어보다 중요한 의미를 포함하고 있다고 볼 수는 없습니다.

물론, 문서에서 빈번하게 등장하는 단어는 문서의 핵심 내용을 담고 있을 수도 있습니다. 하지만 관사 ‘a’나 ‘the’를 생각해 본다면 빈번하게 등장하는 단어가 꼭 중요한 의미를 가지고 있지는 않다는 것을 쉽게 이해할 수 있습니다.

기존 Skip-gram의 보완 방법

그래서 Word2vec은 위의 세 문제를 보완하기 위해 세 가지 전략을 제시합니다.

구(phrase)를 represent하는 방식으로 학습을 진행
Negative sampling 사용
Subsampling 사용

이제 각각의 아이디어들이 구체적으로 무엇을 의미하는지 살펴보겠습니다.

첫번째 아이디어 : Phrase 기반 학습

빈번하게 함께 등장하지만 다른 문맥에서는 드물게 함께 등장하는 단어들의 phrase를 unique token으로 설정하자

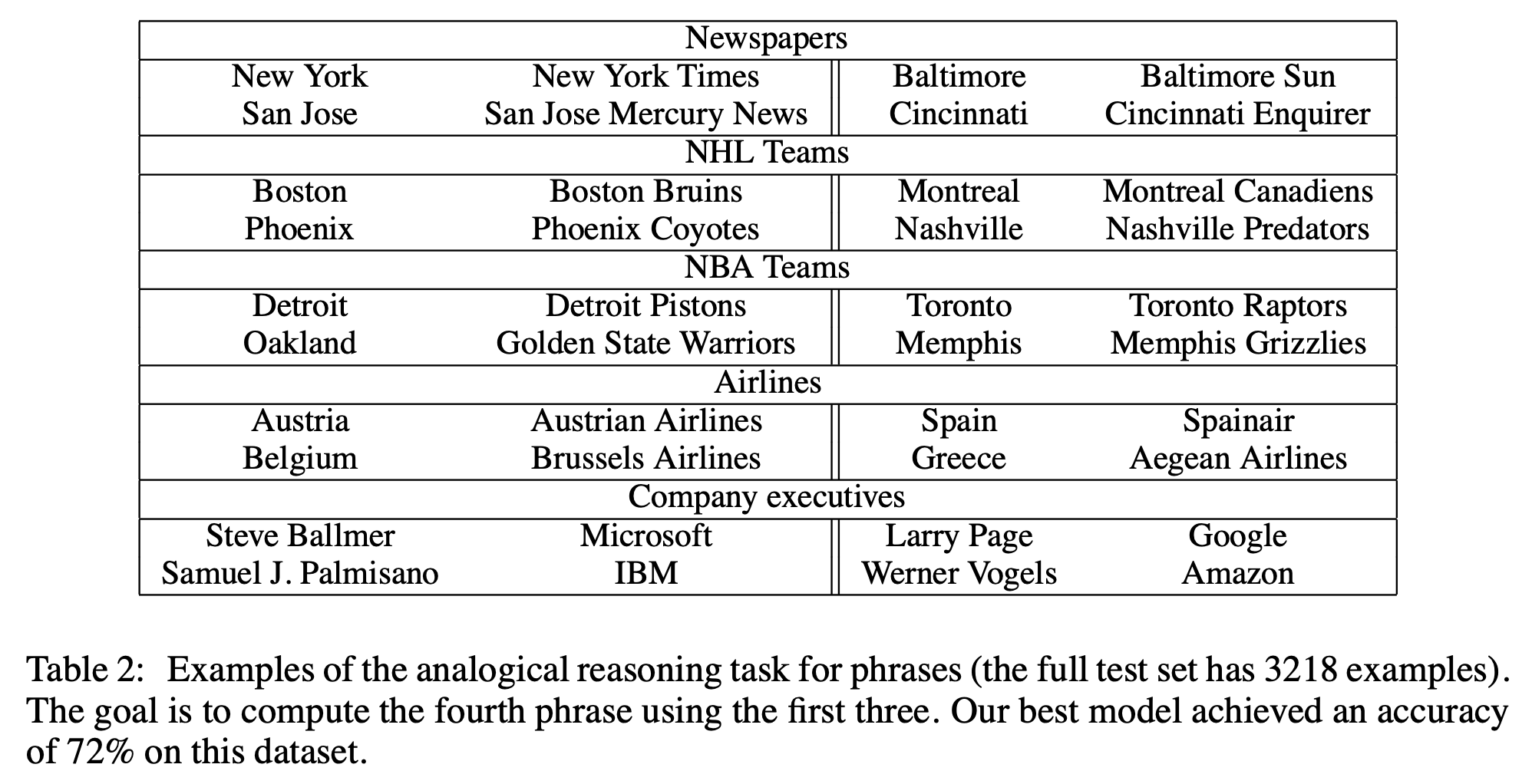
예를 들어, ‘New York’과 ‘Times’ 은 다른 문맥에서는 함께 잘 등장하지 않지만 ‘New York Times’라는 phrase로는 잘 등장합니다. 이를 바탕으로 score 함수를 다음과 같이 작성합니다.

\[\text{score}(w_i, w_j)=\frac{\text{count}(w_i, w_j)-\delta}{\text{count}(w_i)\times \text{count}(w_j)}\]

$\delta$ : 할인 계수(discounting coefficient)로 빈번하지 않은 단어들의 조합으로 구성된 phrase를 학습에 사용하는 것을 방지합니다.

이렇게 계산된 score가 일정 threshold를 넘는 phrase들만 학습에 사용하는데요, 학습에 실제 사용된 phrase의 조합들은 링크 에서 확인할 수 있습니다.

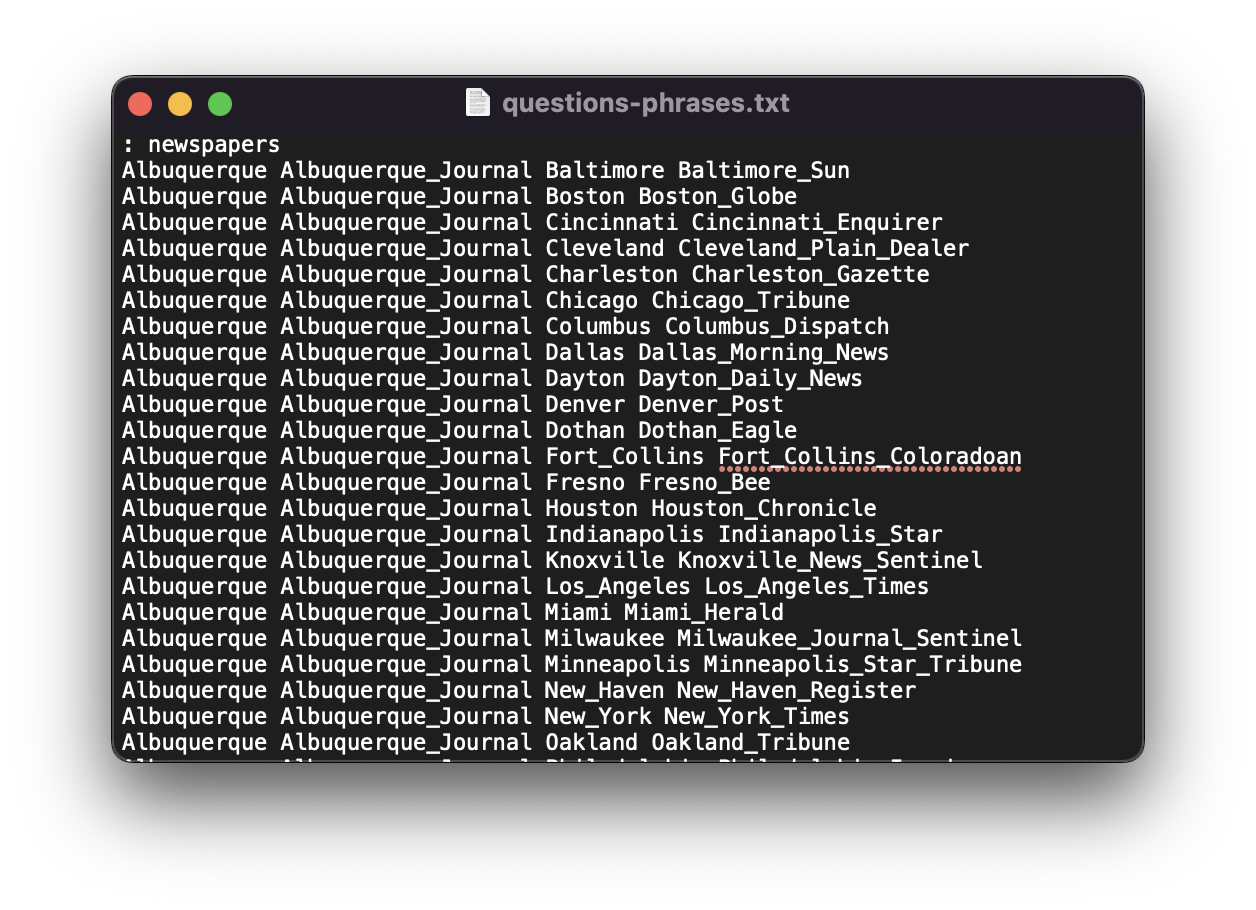
이렇게 단어 기반이 아니라 관용구들을 이용한 phrase 기반 학습을 진행하면 representation quality를 더 높일 수 있다고 합니다.

두번째 아이디어 : Negative sampling (NEG) 사용

기존 Skip-gram의 objective function

Target word가 주어졌을 때, context word를 잘 예측하는 일이 문장 전반에 걸쳐 잘 일어나게 하고 싶다

$\max \frac{1}{T}\sum_{t=1}^T\sum_{-c\le j\le c \ \ (j\neq0)}\log P(w_{t+j}|w_t)$

$w_t$ : Target word (center word)
$w_{t+j}$ : Context word (surrounding word)
$c$ : Window size, target word 주위 몇 개의 단어를 context word로 포함할 것인지 범위를 지정하는 역할
$T$ : 분석하고자 하는 문장(sequence)의 길이

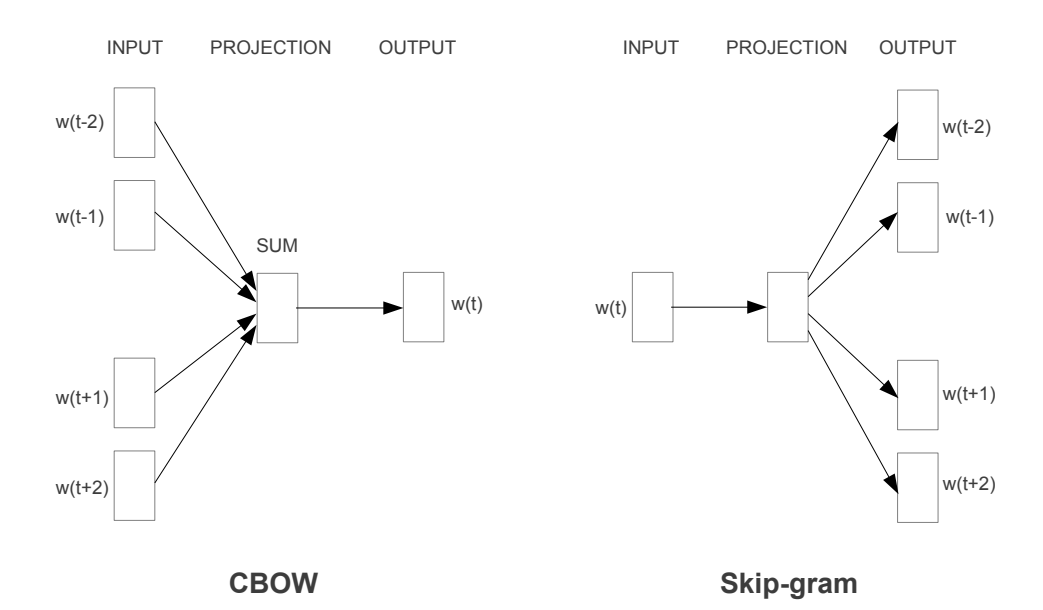
Skip-gram 이전에 등장했던 CBOW는 왼쪽처럼 context 단어들이 주어졌을 때 target 단어를 잘 예측하는 task를 수행했습니다. 하지만 Skip-gram은 반대의 task를 수행하는데요, ‘target 단어가 주어졌을 때 context 단어들을 잘 예측하기’를 수행합니다.

예를 들어 ‘The quick brown fox jumped over the lazy dog’이라는 문장이 있다고 해 보겠습니다. 여기서 target word와 window size를 다음처럼 설정할게요.

Target word $w_t$ : fox
Window size $c$ : 2

그러면 위 문장의 input word와 output word의 조합은 이렇게 생성됩니다.

(fox, quick)
(fox, brown)
(fox, jumped)
(fox, over)

기존 Skip-gram의 hierarchical softmax

원래 Skip-gram에서 사용하려던 softmax function은 다음과 같습니다.

\[\max \frac{1}{T}\sum_{t=1}^T\sum_{-c\le j\le c \ \ (j\neq0)}\log P(w_{t+j}|w_t)\]

여기서 사용하는 $P(w_{t+j}

w_t)$은 0과 1 사이의 확률값으로 나타낼 수 있습니다.

\[P(W_O|W_I)=\frac{\exp({V'_{w_O}}^TV_{w_I})}{\sum_{w=1}^W\exp({V'_w}^TV_{w_I})}\]

이 방식은 objective function을 optimize하기 위해서 $\nabla \log P(W_O

W_I)$를 사용합니다. 그런데 이것의 분모를 계산하기 위해서 많은 연산량이 든다는 한계가 생기게 됩니다.

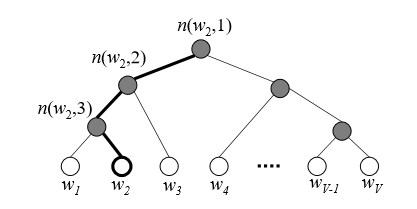
이를 극복하기 위해 등장한 것이 hierarchical softmax인데요, 예를 들어 target word가 $w_2$라고 하면 출발지점(root)에서 target word까지 닿는 데 만나는 모든 node들을 내적합니다.

$p(w|w_I)=\prod_{j=1}^{L(w)-1}\sigma([n(w,j+1)=\ch(n(w,j)]\cdot {v'_{n(w,j)}}^Tv_{w_I}) \\ \text{where} \\\ [x]=1 \ \ \ \text{if} \ \ x \ \ \text{is true, -1 otherwise}$

$n$ : node
$\ch$ : child node

예를 들어 $n(w_2,1)$의 child node가 $n(w_2,2)$와 일치하다면 1, 그렇지 않다면 -1을 부여합니다. 이는 다음의 세 가지 특징을 가집니다.

Root에서 leaf까지 가는 경로를 확률 계산에 사용하는 아이디어
Binary tree structure 이용 → softmax function 구조(일부/전체 = 확률)를 사용하지 않음 → 연산량 감소
Softmax function 대신 sigmoid function $\sigma$를 사용해 확률로 만들어 줌

Negative sampling의 도입

Noise Contrasive Estimation을 일부 단어에만 적용해 연산량을 감소시키자.

Noise Contrastive Eestimation은 무엇일까요? 간단히 말해 실제 data distribution으로부터 얻은 sample과 noise distribution으로부터 얻은 sample을 잘 구분할 수 있도록 하는 것입니다. 하지만 이 때에도 여전히 softmax function을 사용하기 때문에 연산량이 많습니다.

반면 Negative sampling은 전체 단어들을 분모로 사용해야 하는 softmax 구조를 사용하지 않습니다. 대신 일부 단어를 sampling해서 학습한 다음 전체에 대해 근사하는 방식을 사용함으로써 연산량이 줄어들게 됩니다. $\log \sigma({v'_{w_O}}^Tv_{w_I})+\sum_{i=1}^k \mathbb E_{w_i\sim P_n(w)}[\log \sigma({-v'_{w_i}}^Tv_{w_I})]$

$P_n(w_i)=\frac{f(w_i)^\frac{3}{4}}{\sum_{j=0}^n(f(w_i))^\frac{3}{4}}$ : window size 밖의 단어가 negative sample로 포함될 확률

그러면 다시 단어를 sampling하는 기준에 대해 생각해 보아야 하는데요, 논문에서는 지정한 window size $c$ 범위에서 정답 단어(positive) + window size에 등장하지 않는 단어(negative) 의 조합으로 sample을 뽑는다고 합니다. 참고로 작은 dataset에서는 5-20개, 큰 dataset에서는 2-5개의 negative sample을 뽑습니다.

세번째 아이디어 : Subsampling 사용

빈번하게 등장한다고 해서 항상 더 정보가 풍부한 것은 아니다.

앞서 말씀드린 것처럼 $\text{count}(\text{france}, \text{paris}) < \text{count}(\text{france}, \text{the})$ 라고 해서 단순히 the가 france에 더 어울리는 context word라고 보기에는 무리가 있습니다. 오히려 (france, paris)의 조합에 더 많은 benefit을 부여하는 것이 타당합니다. 그래서 논문에서는 마지막으로 빈번하게 등장하는 단어들과 드물게 등장하는 단어들 사이의 불균형을 해소하고자 하였습니다. $P(w_i)=1-\sqrt{\frac{t}{f(w_i)}}$

$P(w_i)$ : 특정 단어 $w_i$가 sampling될 확률
$f(w_i)$ : frequency of word
$t$ : threshold, 대략 $10^{-5}$

많이 등장하는 단어($f(w_i)$가 큰 단어)는 subsampling 과정에서 탈락될(discarded) 확률이 높아지게 됩니다. 이는 학습률과 학습 속도의 상승으로 이어진다고 논문에서 소개합니다.

Back to Posts

Distributed Representations of Words and Phrases and their Compositionality

목차